Wir finden die N-te Fibonacci-Zahl in angemessener Zeit auf drei Arten: die Grundlagen der dynamischen Programmierung. Wir finden die N-te Fibonacci-Zahl in angemessener Zeit auf drei Arten: die Grundlagen der dynamischen Programmierung Rekursive Berechnung der n-ten Zahl der Fibonacci-Reihe

Programmierer sollten die Fibonacci-Zahlen jetzt satt haben. Beispiele für ihre Berechnung werden überall verwendet. Dies liegt daran, dass diese Zahlen das einfachste Beispiel für Rekursion sind. Sie sind auch ein gutes Beispiel für dynamische Programmierung. Aber muss man sie in einem realen Projekt so berechnen? Nicht nötig. Weder Rekursion noch dynamische Programmierung sind ideale Optionen. Und keine geschlossene Formel mit Gleitkommazahlen. Jetzt werde ich Ihnen sagen, wie Sie es richtig machen. Aber lassen Sie uns zuerst alle bekannten Lösungen durchgehen.

Der Code ist für Python 3, obwohl er auch für Python 2 gehen sollte.

Lassen Sie mich zunächst an die Definition erinnern:

Fn = Fn-1 + Fn-2

Und F 1 = F 2 = 1.

Geschlossene Formel

Wir überspringen die Details, wer möchte, kann sich aber mit der Herleitung der Formel vertraut machen. Die Idee ist, anzunehmen, dass es ein x gibt, für das F n = x n ist, und dann x zu finden.

Was bedeutet

Reduziere x n-2

Wir lösen die quadratische Gleichung:

Woher wächst der „goldene Schnitt“ aus ϕ = (1 + √5) / 2. Wenn wir die Anfangswerte ersetzen und einige weitere Berechnungen durchführen, erhalten wir:

Damit berechnen wir F n .

Von __future__ import division import math def fib (n): SQRT5 = math.sqrt (5) PHI = (SQRT5 + 1) / 2 return int (PHI ** n / SQRT5 + 0.5)

Gut:
Schnell und einfach für kleine n
Schlecht:
Gleitkommaoperationen erforderlich. Große n erfordern mehr Präzision.
Böse:
Komplexe Zahlen zur Berechnung von F n zu verwenden ist aus mathematischer Sicht schön, aber aus Computersicht hässlich.

Rekursion

Die offensichtlichste Lösung, die Sie schon oft gesehen haben, ist höchstwahrscheinlich ein Beispiel dafür, was Rekursion ist. Ich werde es der Vollständigkeit halber noch einmal wiederholen. In Python kann es in eine Zeile geschrieben werden:

Fib = Lambda n: fib (n - 1) + fib (n - 2) wenn n> 2 sonst 1

Gut:
Sehr einfache Implementierung, die die mathematische Definition wiederholt
Schlecht:
Exponentielle Ausführungszeit. Sehr langsam für große n
Böse:
Paketüberfluss

Auswendiglernen

Die rekursive Lösung hat ein großes Problem: sich überschneidende Berechnungen. Beim Aufruf von fib (n) werden fib (n-1) und fib (n-2) gezählt. Aber wenn fib (n-1) gezählt wird, wird es wieder unabhängig fib (n-2) zählen - das heißt, fib (n-2) wird zweimal gezählt. Wenn wir die Argumentation fortsetzen, werden wir sehen, dass fib (n-3) dreimal gezählt wird und so weiter. Zu viele Kreuzungen.

Daher müssen Sie sich die Ergebnisse nur merken, um sie nicht erneut zu zählen. Zeit und Speicher für diese Lösung werden auf lineare Weise verbraucht. Ich verwende ein Wörterbuch in der Lösung, aber ein einfaches Array hätte auch verwendet werden können.

M = (0: 0, 1: 1) def fib (n): wenn n in M: Rückgabe M [n] M [n] = fib (n - 1) + fib (n - 2) Rückgabe M [n]

(In Python kann dies auch mit dem Dekorator functools.lru_cache erfolgen.)

Gut:
Verwandeln Sie einfach Rekursion in eine Erinnerungslösung. Konvertiert die exponentielle Ausführungszeit in eine lineare Zeit, wodurch mehr Speicher verbraucht wird.
Schlecht:
Verschwendet viel Speicher
Böse:
Möglicher Stapelüberlauf, wie Rekursion

Dynamische Programmierung

Nach der Entscheidung mit Erinnern wird klar, dass wir nicht alle bisherigen Ergebnisse benötigen, sondern nur die letzten beiden. Alternativ können Sie, anstatt bei fib (n) zu beginnen und rückwärts zu gehen, bei fib (0) beginnen und vorwärts gehen. Der folgende Code hat eine lineare Ausführungszeit und einen festen Speicherverbrauch. In der Praxis wird die Lösungsgeschwindigkeit sogar noch höher ausfallen, da keine rekursiven Funktionsaufrufe und damit verbundene Arbeiten anfallen. Und der Code sieht einfacher aus.

Diese Lösung wird oft als Beispiel für dynamische Programmierung genannt.

Def fib (n): a = 0 b = 1 für __ im Bereich (n): a, b = b, a + b Rückgabe a

Gut:
Funktioniert schnell für kleine n, einfacher Code
Schlecht:
Noch lineare Laufzeit
Böse:
Nichts Besonderes.

Matrixalgebra

Und schließlich die am wenigsten beleuchtete, aber die richtige Lösung, die sowohl Zeit als auch Speicher sinnvoll nutzt. Sie kann auch auf jede homogene lineare Folge erweitert werden. Die Idee ist, Matrizen zu verwenden. Es reicht, das nur zu sehen

Eine Verallgemeinerung legt nahe, dass

Die beiden Werte für x, die wir zuvor erhalten haben, von denen einer der Goldene Schnitt war, sind die Eigenwerte der Matrix. Daher besteht eine andere Möglichkeit, eine geschlossene Formel abzuleiten, darin, eine Matrixgleichung und lineare Algebra zu verwenden.

Warum ist eine solche Formulierung sinnvoll? Die Tatsache, dass die Exponentiation in logarithmischer Zeit erfolgen kann. Dies geschieht durch Quadrieren. Die Quintessenz ist das

Wobei der erste Ausdruck für gerades A verwendet wird, der zweite für ungerade. Es bleibt nur noch die Matrixmultiplikation zu organisieren, und Sie sind fertig. Es stellt sich der folgende Code heraus. Ich habe eine rekursive Implementierung von pow organisiert, weil es einfacher zu verstehen ist. Sehen Sie sich die iterative Version hier an.

Def pow (x, n, I, mult): "" "Gibt x hoch n zurück. Nimmt an, dass I die Identitätsmatrix multipliziert mit mult und n eine positive ganze Zahl ist" "" if n == 0: return I elif n == 1: Rückgabe x else: y = pow (x, n // 2, I, mult) y = mult (y, y) if n% 2: y = mult (x, y) Rückgabe y def identity_matrix ( n): "" "Gibt die n-mal-n-Identitätsmatrix zurück" "" r = list (range (n)) return [for j in r] def matrix_multiply (A, B): BT = list (zip (* B ) ) return [für row_a in A] def fib (n): F = pow ([,], n, identity_matrix (2), matrix_multiply) return F

Gut:
Feste Speichergröße, logarithmische Zeit
Schlecht:
Komplexerer Code
Böse:
Wir müssen mit Matrizen arbeiten, obwohl sie nicht so schlimm sind

Leistungsvergleich

Es lohnt sich nur, die Variante der dynamischen Programmierung und die Matrix zu vergleichen. Wenn wir sie nach der Anzahl der Stellen in der Zahl n vergleichen, stellt sich heraus, dass die Matrixlösung linear und die Lösung mit dynamischer Programmierung exponentiell ist. Ein praktisches Beispiel ist die Berechnung von fib (10 ** 6), einer Zahl mit mehr als zweihunderttausend Zeichen.

N = 10 ** 6
Berechnen Sie fib_matrix: fib (n) hat insgesamt 208988 Stellen, die Berechnung dauerte 0,24993 Sekunden.
Berechnen Sie fib_dynamic: fib (n) hat insgesamt 208988 Stellen, die Berechnung dauerte 11,83377 Sekunden.

Theoretische Bemerkungen

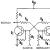
Diese Bemerkung, die den obigen Code nicht direkt berührt, ist dennoch von Interesse. Betrachten Sie die folgende Grafik:

Zählen wir die Anzahl der Pfade der Länge n von A nach B. Zum Beispiel haben wir für n = 1 einen Pfad, 1. Für n = 2 haben wir wieder einen Pfad, 01. Für n = 3 haben wir zwei Pfade, 001 und 101 Man kann ganz einfach zeigen, dass die Anzahl der Wege der Länge n von A nach B genau gleich F n ist. Wenn wir die Adjazenzmatrix für den Graphen aufschreiben, erhalten wir dieselbe Matrix, die oben beschrieben wurde. Dies ist ein bekanntes Ergebnis aus der Graphentheorie, dass für eine gegebene Adjazenzmatrix A die Vorkommen in A n die Anzahl der Pfade der Länge n im Graphen sind (eines der Probleme, die im Film "Good Will Hunting" erwähnt wurden).

Warum gibt es solche Markierungen an den Kanten? Es stellt sich heraus, dass Sie beim Betrachten einer unendlichen Folge von Zeichen auf einer in beide Richtungen unendlichen Folge von Pfaden in einem Graphen etwas namens "Subshifts vom endlichen Typ" erhalten, das eine Art symbolisches Dynamiksystem ist. Diese besondere Unterverschiebung des letzten Typs ist als „Golden-Ratio-Verschiebung“ bekannt und wird durch eine Reihe von „verbotenen Wörtern“ (11) spezifiziert. Mit anderen Worten, wir erhalten in beide Richtungen unendliche binäre Folgen und keine Paare davon werden benachbart sein. Die topologische Entropie dieses dynamischen Systems ist gleich dem Goldenen Schnitt ϕ. Es ist interessant, wie diese Zahl in verschiedenen Bereichen der Mathematik periodisch erscheint.

Fibonacci-Zahlen Ist eine Zahlenreihe, bei der jede nächste Zahl gleich der Summe der beiden vorherigen ist: 1, 1, 2, 3, 5, 8, 13, .... Manchmal beginnt die Reihe bei Null: 0, 1, 1, 2, 3, 5, .... In diesem Fall bleiben wir bei der ersten Option.

Formel:

F1 = 1
F2 = 1
Fn = Fn-1 + Fn-2

Berechnungsbeispiel:

F3 = F2 + F1 = 1 + 1 = 2
F4 = F3 + F2 = 2 + 1 = 3
F 5 = F 4 + F 3 = 3 + 2 = 5
F 6 = F 5 + F 4 = 5 + 3 = 8
...

Berechnung der n-ten Zahl einer Fibonacci-Reihe mit einer while-Schleife

1. Weisen Sie den Variablen fib1 und fib2 die Werte der ersten beiden Elemente der Zeile zu, dh weisen Sie den Variablen Einheiten zu.
2. Fragen Sie den Benutzer nach der Nummer des Elements, dessen Wert er abrufen möchte. Weisen Sie der Variablen n eine Zahl zu.
3. Führen Sie die folgenden Schritte n - 2 mal durch, da die ersten beiden Elemente bereits berücksichtigt wurden:
   1. Fügen Sie fib1 und fib2 hinzu und weisen Sie das Ergebnis einer temporären Speichervariablen zu, beispielsweise fib_sum.
   2. Setzen Sie die Variable fib1 auf fib2.
   3. Setzen Sie die Variable fib2 auf fib_sum.
4. Zeigen Sie den fib2-Wert an.

Notiz. Wenn der Benutzer 1 oder 2 eingibt, wird der Schleifenkörper nie ausgeführt, der ursprüngliche Wert von fib2 wird angezeigt.

fib1 = 1 fib2 = 1 n = Eingabe () n = int (n) i = 0 während i< n - 2 : fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print (fib2)

Kompaktversion des Codes:

fib1 = fib2 = 1 n = int (Eingabe ( "Elementnummer der Fibonacci-Reihe:")) - 2 während n> 0: fib1, fib2 = fib2, fib1 + fib2 n - = 1 print (fib2)

Fibonacci-Zahlen mit einer for-Schleife ausgeben

In diesem Fall wird nicht nur der Wert des benötigten Elements der Fibonacci-Reihe angezeigt, sondern alle Zahlen bis einschließlich. Dazu wird die Ausgabe des fib2-Wertes in eine Schleife gelegt.

fib1 = fib2 = 1 n = int (Eingabe ()) wenn n< 2 : quit() print (fib1, end= " " ) print (fib2, end= " " ) for i in range (2 , n) : fib1, fib2 = fib2, fib1 + fib2 print (fib2, end= " " ) print ()

Ausführungsbeispiel:

10 1 1 2 3 5 8 13 21 34 55

Rekursive Berechnung der n-ten Zahl der Fibonacci-Reihe

1. Wenn n = 1 oder n = 2 ist, geben Sie eins an den aufrufenden Zweig zurück, da das erste und das zweite Element der Fibonacci-Reihe gleich eins sind.
2. In allen anderen Fällen rufen Sie dieselbe Funktion mit den Argumenten n - 1 und n - 2 auf. Addieren Sie das Ergebnis der beiden Aufrufe und geben Sie es an den aufrufenden Programmzweig zurück.

def fibonacci (n): if n in (1, 2): Rückgabe 1 Rückgabe Fibonacci (n - 1) + Fibonacci (n - 2) print (fibonacci (10))

Sagen wir n = 4. Dadurch werden Fibonacci (3) und Fibonacci (2) rekursiv aufgerufen. Die zweite gibt eins zurück, und die erste führt zu zwei weiteren Funktionsaufrufen: fibonacci (2) und fibonacci (1). Beide Anrufe geben einen zurück, insgesamt also zwei. Somit gibt der Aufruf von Fibonacci (3) die Zahl 2 zurück, die zur Zahl 1 aus dem Aufruf von Fibonacci (2) addiert wird. Ergebnis 3 wird an den Mainstream zurückgegeben. Das vierte Element der Fibonacci-Reihe ist gleich drei: 1 1 2 3.

Sehr oft stoßen bei verschiedenen Olympiaden solche Probleme auf, die, wie es auf den ersten Blick scheint, mit einer einfachen Suche gelöst werden können. Zählen wir aber die Anzahl der möglichen Optionen, dann werden wir sofort von der Ineffizienz dieses Ansatzes überzeugt: Beispielsweise verbraucht die untenstehende einfache rekursive Funktion bereits bei der 30. Fibonacci-Zahl erhebliche Ressourcen, während bei den Olympiaden die Lösungszeit ist oft auf 1-5 Sekunden begrenzt.

Int fibo (int n) (if (n == 1 || n == 2) (return 1;) else (return fibo (n - 1) + fibo (n - 2);))

Denken wir darüber nach, warum dies geschieht. Um zum Beispiel fibo (30) zu berechnen, berechnen wir zuerst fibo (29) und fibo (28). Aber gleichzeitig "vergisst" unser Programm, dass fibo (28) wir schon rausgefunden bei der Suche nach Fibo (29).

Der Hauptfehler eines solchen Ansatzes "frontal" besteht darin, dass die gleichen Werte der Funktionsargumente viele Male berechnet werden - und das sind ziemlich ressourcenintensive Operationen. Um sich wiederholende Berechnungen loszuwerden, hilft uns die dynamische Programmiermethode - dies ist eine Technik, bei der ein Problem in allgemeine und sich wiederholende Teilaufgaben unterteilt wird, die jeweils nur einmal gelöst werden - dies erhöht die Effizienz des Programms erheblich. Dieses Verfahren wird ausführlich beschrieben in, es gibt auch Beispiele zur Lösung anderer Probleme.

Der einfachste Weg, unsere Funktion zu verbessern, besteht darin, sich daran zu erinnern, welche Werte wir bereits berechnet haben. Dazu müssen wir ein zusätzliches Array einführen, das als eine Art "Cache" für unsere Berechnungen dient: Bevor wir einen neuen Wert berechnen, prüfen wir, ob wir ihn schon einmal berechnet haben. Wenn wir berechnet haben, nehmen wir den fertigen Wert aus dem Array, und wenn wir ihn nicht berechnet haben, müssen wir ihn basierend auf den vorherigen berechnen und uns für die Zukunft merken:

Int-Cache; int fibo (int n) (if (cache [n] == 0) (if (n == 1 || n == 2) (cache [n] = 1;) else (cache [n] = fibo (n - 1) + fibo (n - 2);)) Cache zurückgeben [n];)

Da wir in dieser Aufgabe zum Berechnen des N-ten Wertes garantiert (N-1) -th benötigen, wird es nicht schwierig sein, die Formel in iterativer Form umzuschreiben - wir füllen unser Array einfach in einer Reihe auf, bis wir das erreichen gewünschte Zelle:

<= n; i++) { cache[i] = cache + cache; } cout << cache;

Jetzt können wir feststellen, dass uns der Wert von F (N-3) bereits garantiert ist, wenn wir den Wert von F (N) berechnen noch nie Wird nicht brauchen. Das heißt, wir müssen nur zwei Werte im Speicher speichern - F (N-1) und F (N-2). Außerdem verliert die Speicherung von F (N-2) jede Bedeutung, sobald wir F (N) berechnet haben. Versuchen wir, diese Gedanken in Form von Code zu schreiben:

// Zwei vorherige Werte: int cache1 = 1; int cache2 = 1; // Neuer Wert int cache3; für (int i = 2; i<= n; i++) { cache3 = cache1 + cache2; //Вычисляем новое значение //Абстрактный cache4 будет равен cache3+cache2 //Значит cache1 нам уже не нужен?.. //Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации. //cache5 = cache4 - cache3 =>Nach der Iteration verliert cache2 seine Relevanz, d.h. es sollte cache1 werden // Mit anderen Worten, cache1 - f (n-2), cache2 - f (n-1), cache3 - f (n). // Sei N = n + 1 (die Zahl, die wir bei der nächsten Iteration berechnen). Dann n-2 = N-3, n-1 = N-2, n = N-1. // Gemäß den neuen Realitäten schreiben wir die Werte unserer Variablen neu: cache1 = cache2; Cache2 = Cache3; ) cout<< cache3;

Ein erfahrener Programmierer versteht, dass der obige Code im Allgemeinen Unsinn ist, da Cache3 nie verwendet wird (er wird sofort in Cache2 geschrieben) und die gesamte Iteration mit nur einem Ausdruck neu geschrieben werden kann:

Cache = 1; Cache = 1; für (int i = 2; i<= n; i++) { cache = cache + cache; //При i=2 устареет 0-й элемент //При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый //При i=4 последним элементом мы обновляли cache, значит ненужное старьё сейчас в cache //Интуитивно понятно, что так будет продолжаться и дальше } cout << cache;

Für diejenigen, die nicht verstehen, wie Magie mit Modulus funktioniert, oder einfach nur eine nicht offensichtliche Formel sehen möchten, gibt es eine andere Lösung:

Intx = 1; int y = 1; für (int i = 2; i< n; i++) { y = x + y; x = y - x; } cout << "Число Фибоначчи: " << y;

Versuchen Sie, die Ausführung dieses Programms zu verfolgen: Sie werden von der Korrektheit des Algorithmus überzeugt sein.

PS Im Allgemeinen gibt es eine einzige Formel zur Berechnung jeder Fibonacci-Zahl, die keine Iteration oder Rekursion erfordert:

Const double SQRT5 = Quadrat (5); const double PHI = (SQRT5 + 1) / 2; int fibo (int n) (return int (pow (PHI, n) / SQRT5 + 0,5);)

Der Haken an der Sache ist jedoch, dass die Berechnung der Potenzen von Nicht-Ganzzahlen ziemlich hoch ist, ebenso wie deren Fehler.