Transponieren einer Matrix in Microsoft Excel. Transponieren einer Matrix in Microsoft Excel Umgekehrtes Transponieren

Matrix A -1 heißt die inverse Matrix bezüglich Matrix A, wenn A*A -1 = E, wobei E die Identitätsmatrix n-ter Ordnung ist. Eine inverse Matrix kann nur für quadratische Matrizen existieren.

Zweck des Dienstes. Mithilfe dieses Dienstes können Sie online algebraische Komplemente, transponierte Matrizen A T, alliierte Matrizen und inverse Matrizen finden. Die Entscheidung wird direkt auf der Website (online) getroffen und ist kostenlos. Die Berechnungsergebnisse werden in einem Bericht im Word- und Excel-Format dargestellt (d. h. es besteht die Möglichkeit, die Lösung zu überprüfen). siehe Designbeispiel.

Anweisungen. Um eine Lösung zu erhalten, ist es notwendig, die Dimension der Matrix anzugeben. Füllen Sie als Nächstes Matrix A im neuen Dialogfeld aus.

Siehe auch Inverse Matrix mit der Jordano-Gauß-Methode

Algorithmus zum Finden der inversen Matrix

1. Finden der transponierten Matrix A T .
2. Definition algebraischer Komplemente. Ersetzen Sie jedes Element der Matrix durch sein algebraisches Komplement.
3. Erstellen einer inversen Matrix aus algebraischen Additionen: Jedes Element der resultierenden Matrix wird durch die Determinante der ursprünglichen Matrix dividiert. Die resultierende Matrix ist die Umkehrung der ursprünglichen Matrix.

Nächste Algorithmus zum Finden der inversen Matrixähnelt dem vorherigen, mit Ausnahme einiger Schritte: Zuerst werden die algebraischen Komplemente berechnet und dann wird die zugehörige Matrix C bestimmt.

1. Bestimmen Sie, ob die Matrix quadratisch ist. Wenn nicht, dann gibt es dafür keine inverse Matrix.
2. Berechnung der Determinante der Matrix A. Ist sie ungleich Null, setzen wir die Lösung fort, andernfalls existiert die inverse Matrix nicht.
3. Definition algebraischer Komplemente.
4. Ausfüllen der Vereinigungsmatrix (gegenseitig, adjungiert) C .
5. Erstellen einer inversen Matrix aus algebraischen Additionen: Jedes Element der adjungierten Matrix C wird durch die Determinante der ursprünglichen Matrix dividiert. Die resultierende Matrix ist die Umkehrung der ursprünglichen Matrix.
6. Sie führen eine Prüfung durch: Sie multiplizieren die Original- und die resultierenden Matrizen. Das Ergebnis sollte eine Identitätsmatrix sein.

Beispiel Nr. 1. Schreiben wir die Matrix in der Form:

Algebraische Ergänzungen. ∆ 1,2 = -(2·4-(-2·(-2))) = -4 ∆ 2,1 = -(2 4-5 3) = 7 ∆ 2,3 = -(-1 5-(-2 2)) = 1 ∆ 3,2 = -(-1·(-2)-2·3) = 4

A -1 =

0,6 -0,4 0,8 0,7 0,2 0,1 -0,1 0,4 -0,3

Ein weiterer Algorithmus zum Finden der inversen Matrix

Lassen Sie uns ein anderes Schema zum Finden der inversen Matrix vorstellen.

1. Finden Sie die Determinante einer gegebenen quadratischen Matrix A.
2. Wir finden algebraische Komplemente zu allen Elementen der Matrix A.
3. Wir schreiben algebraische Additionen von Zeilenelementen zu Spalten (Transposition).
4. Wir dividieren jedes Element der resultierenden Matrix durch die Determinante der Matrix A.

Wie wir sehen, kann die Transpositionsoperation sowohl am Anfang auf die Originalmatrix als auch am Ende auf die resultierenden algebraischen Additionen angewendet werden.

Ein Sonderfall: Die Umkehrung der Identitätsmatrix E ist die Identitätsmatrix E.

Um eine Matrix zu transponieren, müssen Sie die Zeilen der Matrix in Spalten schreiben.

Wenn , dann die transponierte Matrix

Wenn, dann

Übung 1. Finden

1. Determinanten quadratischer Matrizen.

Für quadratische Matrizen wird eine Zahl eingeführt, die Determinante genannt wird.

Für Matrizen zweiter Ordnung (Dimension) ergibt sich die Determinante durch die Formel:

Für eine Matrix beispielsweise lautet ihre Determinante

Beispiel . Berechnen Sie Determinanten von Matrizen.

Für quadratische Matrizen dritter Ordnung (Dimension) gibt es eine „Dreiecks“-Regel: In der Abbildung bedeutet die gepunktete Linie, die Zahlen zu multiplizieren, durch die die gepunktete Linie verläuft. Die ersten drei Zahlen müssen addiert werden, die nächsten drei Zahlen müssen subtrahiert werden.

Beispiel. Berechnen Sie die Determinante.

Um eine allgemeine Definition einer Determinante zu geben, ist es notwendig, das Konzept eines Nebenkomplements und eines algebraischen Komplements einzuführen.

Unerheblich Element der Matrix wird als Determinante bezeichnet, die durch Durchstreichen dieser Zeile und dieser Spalte erhalten wird.

Beispiel. Lassen Sie uns einige Minderjährige der Matrix A finden.

Algebraisches Komplement Element heißt Zahl.

Das heißt, wenn die Summe der Indizes gerade ist, unterscheiden sie sich nicht. Ist die Summe der Indizes ungerade, dann unterscheiden sie sich nur im Vorzeichen.

Für das vorherige Beispiel.

Matrixdeterminante ist die Summe der Produkte der Elemente einer bestimmten Zeichenfolge

(Spalte) zu ihren algebraischen Komplementen. Betrachten wir diese Definition auf einer Matrix dritter Ordnung.

Der erste Eintrag wird als Entwicklung der Determinante in der ersten Zeile bezeichnet, der zweite ist die Entwicklung in der zweiten Spalte und der letzte ist die Entwicklung in der dritten Zeile. Insgesamt können solche Erweiterungen sechsmal geschrieben werden.

Beispiel. Berechnen Sie die Determinante mithilfe der „Dreiecksregel“ und erweitern Sie sie entlang der ersten Zeile, dann entlang der dritten Spalte und dann entlang der zweiten Zeile.

Erweitern wir die Determinante entlang der ersten Zeile:

Erweitern wir die Determinante in der dritten Spalte:

Erweitern wir die Determinante entlang der zweiten Zeile:

Beachten Sie, dass die Berechnungen umso einfacher sind, je mehr Nullen vorhanden sind. Wenn wir beispielsweise um die erste Spalte erweitern, erhalten wir

Unter den Eigenschaften von Determinanten gibt es eine Eigenschaft, die es ermöglicht, Nullen zu erhalten, nämlich:

Wenn Sie Elemente einer anderen Zeile (Spalte) zu den Elementen einer bestimmten Zeile (Spalte) hinzufügen und mit einer Zahl ungleich Null multiplizieren, ändert sich die Determinante nicht.

Nehmen wir dieselbe Determinante und erhalten beispielsweise Nullen in der ersten Zeile.

Determinanten höherer Ordnung werden auf die gleiche Weise berechnet.

Aufgabe 2. Berechnen Sie die Determinante vierter Ordnung:

1) über eine beliebige Zeile oder Spalte verteilen

2) nachdem zuvor Nullen erhalten wurden

In der zweiten Spalte erhalten wir beispielsweise eine zusätzliche Null. Multiplizieren Sie dazu die Elemente der zweiten Zeile mit -1 und addieren Sie sie zur vierten Zeile:

1. Lösen von Systemen linearer algebraischer Gleichungen mit der Cramer-Methode.

Wir zeigen die Lösung eines Systems linearer algebraischer Gleichungen mit der Methode von Cramer.

Aufgabe 2. Lösen Sie das Gleichungssystem.

Wir müssen vier Determinanten berechnen. Der erste wird als Hauptfaktor bezeichnet und besteht aus Koeffizienten für die Unbekannten:

Beachten Sie, dass das System nicht mit der Methode von Cramer gelöst werden kann.

Die drei verbleibenden Determinanten werden mit , bezeichnet und erhalten, indem die entsprechende Spalte durch eine Spalte mit rechten Seiten ersetzt wird.

Wir finden. Ändern Sie dazu die erste Spalte in der Hauptdeterminante in eine Spalte mit rechten Seiten:

Wir finden. Ändern Sie dazu die zweite Spalte in der Hauptdeterminante in eine Spalte mit rechten Seiten:

Wir finden. Ändern Sie dazu die dritte Spalte in der Hauptdeterminante in eine Spalte mit rechten Seiten:

Wir finden die Lösung des Systems mithilfe der Cramer-Formeln: , ,

Somit lautet die Lösung des Systems:

Führen wir eine Überprüfung durch; dazu ersetzen wir die gefundene Lösung in allen Gleichungen des Systems.

1. Lösen von Systemen linearer algebraischer Gleichungen mit der Matrixmethode.

Wenn eine quadratische Matrix eine Determinante ungleich Null hat, gibt es eine inverse Matrix mit . Die Matrix wird Identitätsmatrix genannt und hat die Form

Die inverse Matrix ergibt sich aus der Formel:

Beispiel. Finden Sie die Umkehrung einer Matrix

Zuerst berechnen wir die Determinante.

Algebraische Komplemente finden:

Wir schreiben die inverse Matrix:

Um die Berechnungen zu überprüfen, müssen Sie sicherstellen, dass .

Gegeben sei ein lineares Gleichungssystem:

Bezeichnen wir

Dann kann das Gleichungssystem in Matrixform geschrieben werden als und daher. Die resultierende Formel wird als Matrixmethode zur Lösung des Systems bezeichnet.

Aufgabe 3. Lösen Sie das System mit der Matrixmethode.

Es ist notwendig, die Matrix des Systems aufzuschreiben, ihre Umkehrung zu finden und sie dann mit der Spalte der rechten Seiten zu multiplizieren.

Wir haben die inverse Matrix bereits im vorherigen Beispiel gefunden, was bedeutet, dass wir eine Lösung finden können:

1. Lösen von Systemen linearer algebraischer Gleichungen mit der Gauß-Methode.

Die Cramer-Methode und die Matrixmethode werden nur für quadratische Systeme verwendet (die Anzahl der Gleichungen ist gleich der Anzahl der Unbekannten) und die Determinante darf nicht gleich Null sein. Wenn die Anzahl der Gleichungen nicht der Anzahl der Unbekannten entspricht oder die Determinante des Systems Null ist, wird die Gaußsche Methode verwendet. Mit der Gaußschen Methode kann jedes System gelöst werden.

Und setzen wir es in die erste Gleichung ein:

Aufgabe 5. Lösen Sie ein Gleichungssystem mit der Gauß-Methode.

Mithilfe der resultierenden Matrix stellen wir das System wieder her:

Wir finden eine Lösung:

Wenn Sie mit Matrizen arbeiten, müssen Sie diese manchmal transponieren, also in einfachen Worten umdrehen. Natürlich können Sie die Daten auch manuell eingeben, Excel bietet jedoch mehrere Möglichkeiten, dies einfacher und schneller zu erledigen. Schauen wir sie uns im Detail an.

Bei der Matrixtransposition handelt es sich um den Vorgang des Vertauschens von Spalten und Zeilen. Excel bietet zwei Möglichkeiten zum Transponieren: die Verwendung der Funktion TRANSSP und mit dem Einsatz-Spezialwerkzeug. Schauen wir uns jede dieser Optionen genauer an.

Methode 1: TRANSPOSE-Operator

Funktion TRANSSP gehört zur Kategorie der Operatoren „Links und Arrays“. Die Besonderheit besteht darin, dass das Ausgabeergebnis wie bei anderen Funktionen, die mit Arrays arbeiten, nicht der Inhalt der Zelle, sondern ein gesamtes Datenarray ist. Die Funktionssyntax ist recht einfach und sieht so aus:

TRANSP(Array)

Das heißt, das einzige Argument dieses Operators ist ein Verweis auf das Array, in unserem Fall die Matrix, das konvertiert werden soll.

Sehen wir uns anhand eines Beispiels mit einer realen Matrix an, wie diese Funktion angewendet werden kann.

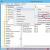
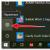
1. Wir wählen eine leere Zelle auf dem Blatt aus, die wir zur obersten linken Zelle der transformierten Matrix machen möchten. Klicken Sie anschließend auf das Symbol „Funktion einfügen“, das sich in der Nähe der Bearbeitungsleiste befindet.



2. Start läuft Funktionsassistenten. Öffnen Sie die Kategorie darin „Links und Arrays“ oder „Vollständige alphabetische Liste“. Nachdem ich den Namen gefunden habe „TRANSP“, wählen Sie es aus und klicken Sie auf die Schaltfläche "OK".



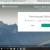
3. Das Fenster mit den Funktionsargumenten wird geöffnet TRANSSP. Das einzige Argument dieses Operators entspricht dem Feld „Array“. Sie müssen die Koordinaten der Matrix eingeben, die umgedreht werden soll. Platzieren Sie dazu den Cursor im Feld und markieren Sie mit gedrückter linker Maustaste den gesamten Bereich der Matrix auf dem Blatt. Nachdem die Bereichsadresse im Argumentfenster angezeigt wird, klicken Sie auf die Schaltfläche "OK".



4. Aber wie wir sehen, wird in der Zelle, die das Ergebnis anzeigen soll, ein falscher Wert in Form eines Fehlers angezeigt "#WERT!". Dies liegt an der Funktionsweise von Array-Operatoren. Um diesen Fehler zu korrigieren, wählen Sie einen Zellbereich aus, in dem die Anzahl der Zeilen gleich der Anzahl der Spalten der ursprünglichen Matrix und die Anzahl der Spalten gleich der Anzahl der Zeilen sein sollte. Eine solche Übereinstimmung ist sehr wichtig, damit das Ergebnis korrekt angezeigt wird. In diesem Fall die Zelle, die den Ausdruck enthält "#WERT!" sollte die obere linke Zelle des ausgewählten Arrays sein und von dieser Zelle aus sollte der Auswahlvorgang beginnen, indem Sie die linke Maustaste gedrückt halten. Nachdem Sie die Auswahl getroffen haben, platzieren Sie den Cursor in der Bearbeitungsleiste direkt nach dem Operatorausdruck TRANSSP, die darin erscheinen sollte. Um die Berechnung durchzuführen, müssen Sie anschließend die Taste drücken Eingeben, wie in herkömmlichen Formeln üblich, und wählen Sie die Kombination Strg+Umschalt+Eingabetaste.



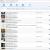
5. Nach diesen Aktionen wurde die Matrix nach Bedarf angezeigt, also in transponierter Form. Aber es gibt noch ein anderes Problem. Tatsache ist, dass die neue Matrix jetzt ein Array ist, das durch eine Formel verknüpft ist, die nicht geändert werden kann. Wenn Sie versuchen, Änderungen am Inhalt der Matrix vorzunehmen, wird eine Fehlermeldung angezeigt. Einige Benutzer sind mit diesem Zustand durchaus zufrieden, da sie keine Änderungen am Array vornehmen möchten, andere benötigen jedoch eine Matrix, mit der sie vollständig arbeiten können.

   Um dieses Problem zu lösen, wählen wir den gesamten transponierten Bereich aus. Wechsel zur Registerkarte "Heim" Klicken Sie auf das Symbol "Kopieren", das sich auf dem Menüband in der Gruppe befindet „Zwischenablage“. Anstelle der angegebenen Aktion können Sie nach der Auswahl eine Standard-Tastenkombination zum Kopieren festlegen Strg+C.



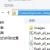
6. Klicken Sie dann mit der rechten Maustaste darauf, ohne die Auswahl aus dem transponierten Bereich zu entfernen. Im Kontextmenü in der Gruppe „Einfügeoptionen“ Klicken Sie auf das Symbol "Werte", das wie ein Piktogramm mit Zahlen aussieht.

   

   Anschließend folgt die Matrixformel TRANSSP wird gelöscht und es verbleiben nur noch ein Wert in den Zellen, mit dem auf die gleiche Weise wie mit der Originalmatrix gearbeitet werden kann.

Methode 2: Matrixtransponierung mit Paste Special

Darüber hinaus kann die Matrix über einen aufgerufenen Kontextmenüpunkt transponiert werden „Spezial einfügen“.

Nach diesen Schritten verbleibt nur noch die transformierte Matrix auf dem Blatt.

Mit denselben beiden oben besprochenen Methoden können Sie nicht nur Matrizen, sondern auch vollwertige Tabellen in Excel übertragen. Der Ablauf wird nahezu identisch sein.

Wir haben also herausgefunden, dass in Excel die Matrix auf zwei Arten transponiert werden kann, also durch Vertauschen von Spalten und Zeilen umgedreht werden kann. Die erste Möglichkeit besteht darin, die Funktion zu verwenden TRANSSP und das zweite ist „Spezialwerkzeuge einfügen“. Im Großen und Ganzen ist das Endergebnis, das bei Verwendung dieser beiden Methoden erzielt wird, nicht unterschiedlich. Beide Methoden funktionieren in fast jeder Situation. Bei der Wahl einer Konvertierungsoption stehen also die persönlichen Vorlieben des jeweiligen Nutzers im Vordergrund. Das heißt, welche dieser Methoden für Sie persönlich bequemer ist, verwenden Sie diese.

Das Umrechnen einer Matrix mit diesem Online-Rechner nimmt nicht viel Zeit in Anspruch, liefert aber schnell Ergebnisse und hilft Ihnen, den Prozess selbst besser zu verstehen.

Manchmal besteht bei algebraischen Berechnungen die Notwendigkeit, die Zeilen und Spalten einer Matrix zu vertauschen. Diese Operation wird Matrixtransposition genannt. Die Zeilen werden in der Reihenfolge zu Spalten und die Matrix selbst wird transponiert. Bei diesen Berechnungen gelten bestimmte Regeln. Um diese zu verstehen und sich visuell mit dem Vorgang vertraut zu machen, verwenden Sie diesen Online-Rechner. Dies wird Ihre Aufgabe erheblich erleichtern und Ihnen helfen, die Theorie der Matrixtransposition besser zu verstehen. Ein wesentlicher Vorteil dieses Rechners ist die Demonstration einer erweiterten und detaillierten Lösung. Somit fördert seine Verwendung ein tieferes und fundierteres Verständnis algebraischer Berechnungen. Darüber hinaus können Sie mit seiner Hilfe jederzeit überprüfen, wie erfolgreich Sie die Aufgabe durch manuelles Transponieren der Matrizen erledigt haben.

Der Rechner ist sehr einfach zu bedienen. Um online eine transponierte Matrix zu finden, geben Sie die Matrixgröße an, indem Sie auf die Symbole „+“ oder „-“ klicken, bis Sie die gewünschte Anzahl von Spalten und Zeilen erhalten. Geben Sie anschließend die erforderlichen Zahlen in die Felder ein. Unten finden Sie die Schaltfläche „Berechnen“. Wenn Sie darauf klicken, wird eine fertige Lösung mit einer detaillierten Erläuterung des Algorithmus angezeigt.