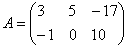Kann die Matrixzeile mit einer Zahl multipliziert werden? Matrixaktionen

Dieses Tool hilft Ihnen beim Erlernen der Leistung aktionen mit Matrizen: Addition (Subtraktion) von Matrizen, Matrixtransposition, Matrixmultiplikation, Auffinden der inversen Matrix. Das gesamte Material wird in einer einfachen und leicht zugänglichen Form präsentiert, relevante Beispiele werden gegeben, so dass auch eine unvorbereitete Person lernen kann, wie man Aktionen mit Matrizen ausführt. Zum Selbstchecken und Selbstchecken können Sie einen kostenlosen Matrixrechner herunterladen \u003e\u003e\u003e.

Ich werde versuchen, die theoretischen Berechnungen zu minimieren, an einigen Stellen gibt es Erklärungen „an den Fingern“ und die Verwendung von unwissenschaftlichen Begriffen. Liebhaber solider Theorie, bitte üben Sie keine Kritik, unsere Aufgabe - erfahren Sie, wie Sie Aktionen mit Matrizen ausführen.

Für die superschnelle Vorbereitung auf das Thema (wer "brennt") gibt es einen intensiven PDF-Kurs Matrix, Determinante und Test!

Die Matrix ist eine rechteckige Tabelle von jedem gegenstände. Als gegenstände  Wir betrachten Zahlen, also numerische Matrizen. ELEMENT  - das ist ein Begriff. Es ist wünschenswert, sich an den Begriff zu erinnern, der häufig vorkommt. Es ist kein Zufall, dass ich ihn durch Fettdruck hervorgehoben habe.

Bezeichnung:  Matrizen werden normalerweise mit lateinischen Großbuchstaben bezeichnet.

Beispiel:  Betrachten Sie die Matrix "zwei mal drei":

Diese Matrix besteht aus sechs gegenstände:

   Alle Zahlen (Elemente) in der Matrix existieren für sich, das heißt, von Subtraktion kann keine Rede sein:

   Dies ist nur eine Tabelle (Menge) von Zahlen!

Stimme auch zu nicht neu anordnen  Zahlen, sofern in den Erläuterungen nichts anderes angegeben ist. Jede Nummer hat ihren eigenen Ort und sie können nicht gemischt werden!

Die fragliche Matrix hat zwei Zeilen:

   und drei Spalten:

STANDARD: wenn sie über die Größe der Matrix sprechen, dann zuerst  Geben Sie die Anzahl der Zeilen und erst dann die Anzahl der Spalten an. Wir haben gerade eine Zwei-mal-Drei-Matrix aussortiert.

Wenn die Anzahl der Zeilen und Spalten der Matrix gleich ist, wird die Matrix aufgerufen platzzum beispiel:   - Matrix "drei mal drei".

Wenn die Matrix eine Spalte oder eine Zeile ist, werden solche Matrizen auch aufgerufen vektoren.

In der Tat kennen wir das Konzept einer Matrix aus der Schule, betrachten Sie zum Beispiel einen Punkt mit den Koordinaten "X" und "Y". Im Wesentlichen werden die Koordinaten eines Punktes in eine Eins-zu-Zwei-Matrix geschrieben. Übrigens, hier ist ein Beispiel, warum die Reihenfolge der Zahlen wichtig ist: und - das sind zwei völlig verschiedene Punkte der Ebene.

Gehen Sie jetzt direkt zum Arbeitszimmer aktion mit Matrizen:

1) Akt eins. Minus aus der Matrix ausführen (Minus in die Matrix eintragen).

Zurück zu unserer Matrix . Wie Sie wahrscheinlich bemerkt haben, enthält diese Matrix zu viele negative Zahlen. Dies ist vom Standpunkt der Ausführung verschiedener Aktionen mit der Matrix aus sehr unbequem, es ist unbequem, so viele Minuspunkte zu schreiben, und es sieht nur im Design hässlich aus.

Wir entfernen das Minus aus der Matrix und ändern das Vorzeichen bei JEDEM Element der Matrix:

   Wie Sie verstehen, ändert sich das Vorzeichen bei Null nicht, in Afrika ist Null gleich Null.

Umgekehrtes Beispiel: . Es sieht hässlich aus.

Wir fügen der Matrix ein Minus hinzu und ändern das Vorzeichen von JEDEM Matrixelement:

Nun, viel schöner ist es passiert. Und vor allem ist es einfacher, Aktionen mit der Matrix auszuführen. Weil es so ein mathematisches Volkszeichen gibt: je mehr Minuspunkte - desto mehr Verwirrung und Fehler.

2) Die zweite Aktion. Matrixmultiplikation mit der Zahl.

Beispiel:

Es ist einfach, um die Matrix mit einer Zahl zu multiplizieren, müssen Sie jeder  Matrixelement multipliziert mit der angegebenen Zahl. In diesem Fall die ersten drei.

Ein weiteres nützliches Beispiel:

  - Matrixmultiplikation mit Bruch

Überlegen Sie zuerst, was zu tun ist. NICHT NÖTIG:

   Es ist nicht notwendig, einen Bruch in der Matrix zu machen, zum einen erschwert dies nur weitere Aktionen mit der Matrix, zum anderen erschwert es dem Lehrer, die Lösung zu überprüfen (insbesondere wenn   - die endgültige Antwort der Aufgabe).

Und darüber hinaus NICHT NÖTIG  dividiere jedes Element der Matrix durch minus sieben:

Aus dem Artikel Mathe für Dummies oder wo ich anfangen sollWir erinnern uns, dass Dezimalstellen mit einem Komma in der höheren Mathematik versuchen, auf jede mögliche Weise zu vermeiden.

Das einzige was das wünschenswert  In diesem Beispiel wird der Matrix ein Minus hinzugefügt:

Aber wenn Alle  Matrixelemente wurden durch 7 geteilt kein Rückstand, dann wäre es möglich (und notwendig!), sich zu teilen.

Beispiel:

In diesem Fall können Sie und Brauchen  multiplizieren Sie alle Elemente der Matrix mit, da alle Zahlen der Matrix durch 2 geteilt werden kein Rückstand.

Anmerkung: In der Theorie der höheren Mathematik ist der Schulbegriff "Division" nicht. Anstelle des Satzes "Teile es in dieses" kann man immer "Multiplizieren mit Bruch" sagen. Das heißt, Division ist ein Spezialfall der Multiplikation.

3) Die dritte Aktion. Matrix transponieren.

Um eine Matrix zu transponieren, müssen Sie ihre Zeilen in die Spalten der transponierten Matrix schreiben.

Beispiel:

Matrix transponieren

Hier gibt es nur eine Zeile, die laut Regel in eine Spalte geschrieben werden sollte:

  - transponierte Matrix.

Die transponierte Matrix wird normalerweise durch einen hochgestellten oder einen Bindestrich oben rechts gekennzeichnet.

Schritt für Schritt Beispiel:

Matrix transponieren

Zuerst schreiben wir die erste Zeile in der ersten Spalte um:

Dann schreiben wir die zweite Zeile in die zweite Spalte:

Und schließlich schreiben wir die dritte Zeile in der dritten Spalte um:

Ist fertig Transponieren bedeutet grob gesagt, die Matrix zur Seite zu drehen.

4) Akt vier. Die Summe (Differenz) der Matrizen.

Die Summe der Matrizen ist einfach.
   NICHT ALLE MATRIXEN KÖNNEN GEFALTET WERDEN. Um die Addition (Subtraktion) von Matrizen durchzuführen, ist es erforderlich, dass sie der Größe entsprechen.

Wenn zum Beispiel eine Zwei-mal-Zwei-Matrix angegeben ist, kann sie nur mit einer Zwei-mal-Zwei-Matrix und keiner anderen hinzugefügt werden!

Beispiel:

Fügen Sie Matrizen hinzu   und

Um die Matrizen hinzuzufügen, müssen ihre jeweiligen Elemente hinzugefügt werden.:

Für die Matrixdifferenz ist die Regel ähnlich: es ist notwendig, den Unterschied der entsprechenden Elemente zu finden.

Beispiel:

Finden Sie den Matrixunterschied ,

Und wie kann man dieses Beispiel leichter lösen, um nicht durcheinander zu kommen? Es ist ratsam, die zusätzlichen Nachteile zu beseitigen. Dazu fügen wir der Matrix ein Minus hinzu:

Hinweis: In der Theorie der höheren Mathematik ist der Schulbegriff "Subtraktion" nicht. Anstelle der Phrase "subtrahiere es davon" kann man immer "füge eine negative Zahl hinzu" sagen. Das heißt, die Subtraktion ist ein Sonderfall der Addition.

5) Die fünfte Aktion. Matrixmultiplikation.

Welche Matrizen können multipliziert werden?

Damit die Matrix mit der Matrix multipliziert werden kann, so dass die Anzahl der Spalten der Matrix gleich der Anzahl der Zeilen der Matrix ist.

Beispiel:
   Ist es möglich, die Matrix mit der Matrix zu multiplizieren?

So können Sie die Datenmatrix multiplizieren.

Aber wenn Matrizen an einigen Stellen neu angeordnet werden, ist in diesem Fall keine Multiplikation mehr möglich!

Daher ist es unmöglich, eine Multiplikation durchzuführen:

Nicht selten gibt es Aufgaben mit einem Trick, wenn ein Schüler aufgefordert wird, Matrizen zu multiplizieren, deren Multiplikation offensichtlich unmöglich ist.

Es ist zu beachten, dass es in einigen Fällen möglich ist, die Matrix und so weiter zu multiplizieren.
   Beispielsweise sind für Matrizen sowohl Multiplikation als auch Multiplikation möglich.

Vorlesung Nummer 1

MATRIX

Definition und Arten von Matrizen

Definition 1.1.Durch die Matrixgröße t nbezeichnet eine rechteckige Tabelle mit Zahlen (oder anderen Objekten), die enthält mreihen und nspalten.

Matrizen werden durch Großbuchstaben des lateinischen Alphabets gekennzeichnet, z. B. A, B, C, ...Die Zahlen (oder andere Objekte), aus denen die Matrix besteht, werden aufgerufen elementematrizen. Matrixelemente können Funktionen sein. Um die Elemente der Matrix anzuzeigen, werden lateinische Kleinbuchstaben mit doppelter Indexierung verwendet: aijwo ist der erste Index ich(Lese - und) - Zeilennummer, zweiter Index j(read - zhi) – spaltennummer.

Definition 1.2.Die Matrix wird aufgerufen quadrat n-ordnung, wenn die Anzahl seiner Zeilen gleich der Anzahl der Spalten und gleich der gleichen Anzahl ist n

Für eine quadratische Matrix werden Konzepte vorgestellt. haupt- und Seitediagonal

Definition 1.3.Hauptdiagonaleeine quadratische Matrix besteht aus Elementen mit denselben Indizes, d.h. Dies sind die Elemente: a11, a 22, ...

Definition 1.4. diagonal, wenn alle Elemente außer den Elementen der Hauptdiagonale gleich Null sind

Definition 1.5.Die quadratische Matrix heißt dreieckigWenn alle Elemente unterhalb (oder oberhalb) der Hauptdiagonale gleich Null sind.

Definition 1.6.Quadratische Matrix p-die Reihenfolge, in der alle Elemente der Hauptdiagonale gleich eins sind und der Rest Null ist, wird aufgerufen singledurch Matrix nth Ordnung, und es wird mit dem Buchstaben bezeichnet E.

Definition 1.7.Eine Matrix beliebiger Größe wird aufgerufen ,oder nullmatrix,wenn alle seine Elemente Null sind.

Definition 1.8.Eine einzelne Zeilenmatrix wird aufgerufen matrixzeile.

Definition 1.9.Eine einzelne Spaltenmatrix wird aufgerufen spaltenmatrix.

A = (a11 a12 ... a1n) -matrixzeile;

Definition 1.10.Zwei Matrizen Aund Inidentische Größen werden genannt gleichwenn alle entsprechenden Elemente dieser Matrizen gleich sind, d.h. aij = bijfür jeden ich= 1, 2, ..., t; j =1, 2,…, n.

Matrix-Operationen

Über Matrizen sowie über Zahlen kann eine Anzahl von Operationen ausgeführt werden. Die Hauptoperationen bei Matrizen sind Addition (Subtraktion) von Matrizen, Multiplikation einer Matrix mit einer Zahl, Multiplikation von Matrizen. Diese Operationen ähneln Operationen mit Zahlen. Eine spezielle Operation ist die Matrixtransposition.

Matrixmultiplikation mit der Zahl

Definition 1.11.Das Produkt der Matrix A zur Zahlλ heißt die Matrix B = A,elemente davon werden durch Multiplikation der Elemente der Matrix erhalten Adurch λ .

Beispiel 1.1.Matrix-Produkt suchen A =   durch die Nummer 5.

Lösung. .◄ 5A =

Matrixmultiplikationsregel mit Zahl: Um die Matrix mit einer Zahl zu multiplizieren, müssen Sie alle Elemente der Matrix mit dieser Zahl multiplizieren.

Die Untersuchung.

1. Der gemeinsame Faktor aller Elemente der Matrix kann aus dem Matrixzeichen entnommen werden.

2. Das Produkt der Matrix Aauf Nummer 0 gibt es eine Nullmatrix: A· 0 = 0 .

Matrixaddition

Definition 1.12.Die Summe zweier Matrizen A und Bgleiche Größe t ndie Matrix genannt Mit= A+ Inderen Elemente erhält man durch Addition der entsprechenden Elemente der Matrix Aund Matrizen Ind.h. cij = aij + bijfür i =1, 2, ..., m; j= 1, 2, ..., n(d.h. Matrizen werden elementweise hinzugefügt).

Die Untersuchung.Matrixsumme Amit Nullmatrix ist gleich der ursprünglichen Matrix: A + O = A.

1.2.3. Matrix-Subtraktion

Der Unterschied zweier Matrizendie gleiche Größe wird durch die vorherigen Operationen bestimmt: A - B = A + (-1).

Definition 1.13.Matrix –A = (-1) Aangerufen gegenübermatrix A.

Die Untersuchung.Die Summe der entgegengesetzten Matrizen ist gleich der Nullmatrix. : A + (–A) = O.

Matrixmultiplikation

Definition 1.14.Multiplikation von Matrix A mit Matrix Bbestimmt, wenn die Anzahl der Spalten der ersten Matrix gleich der Anzahl der Zeilen der zweiten Matrix ist. Dann matrixprodukteine solche Matrix genannt , jedes Element davon cijgleich der Summe der Produkte der Elemente ichZeilenmatrix Aauf zusammenpassende Einzelteile jMatrix Matrix B.

Beispiel 1.4.Berechnen Sie das Produkt der Matrizen A · B,wo

A =

=

Beispiel 1.5.Finden Sie Matrix Works ABund WA,wo

Bemerkungen.Aus den Beispielen 1.4-1.5 folgt, dass die Operation zum Multiplizieren von Matrizen einige Unterschiede zur Multiplikation von Zahlen aufweist:

1) wenn das Produkt von Matrizen ABexistiert dann nach Umordnung der Faktoren das Produkt der Matrizen VAkann nicht existieren. Tatsächlich existiert in Beispiel 1.4 das Produkt der Matrizen AB und das Produkt BA existiert nicht;

2) auch wenn es funktioniert ABund VAexistieren, kann das Ergebnis des Produkts Matrizen unterschiedlicher Größe sein. In dem Fall, wenn beides funktioniert ABund VAes gibt beide - Matrizen gleicher Größe (dies ist nur möglich, wenn quadratische Matrizen gleicher Ordnung multipliziert werden) das kommutative (austauschbare) Multiplikationsgesetz ist immer noch nicht erfüllt,d.h. A b In A wie in Beispiel 1.5;

3) Wenn Sie jedoch eine quadratische Matrix multiplizieren Apro Einheitsmatrix Egleiche Reihenfolge dann AE = EA = A.

Wenn also Matrizen multipliziert werden, spielt die Identitätsmatrix beim Multiplizieren von Zahlen die gleiche Rolle wie die Zahl 1;

4) Das Produkt von zwei Nicht-Null-Matrizen kann gleich der Null-Matrix sein, d. H. Aufgrund der Tatsache, dass A b= 0, das folgt nicht A =0 oder B =0.

Dieses Thema behandelt Operationen wie Addition und Subtraktion von Matrizen, Matrixmultiplikation mit einer Zahl, Matrixmultiplikation mit einer Matrix, Matrixtransposition. Alle Bezeichnungen, die auf dieser Seite verwendet werden, stammen aus dem vorherigen Thema.

  Addition und Subtraktion von Matrizen.

Die Summe von $ A + B $ Matrizen $ A_ (m \\ times n) = (a_ (ij)) $ und $ B_ (m \\ times n) = (b_ (ij)) $ ist die Matrix $ C_ (m \\ times n) = (c_ (ij)) $, wobei $ c_ (ij) = a_ (ij) + b_ (ij) $ für alle $ i = \\ overline (1, m) $ und $ j = \\ overline (1, n) $.

Eine ähnliche Definition wird für die Differenz der Matrizen eingeführt:

Die Differenz $ AB $ der Matrizen $ A_ (m \\ times n) = (a_ (ij)) $ und $ B_ (m \\ times n) = (b_ (ij)) $ ist die Matrix $ C_ (m \\ times n) = ( c_ (ij)) $, wobei $ c_ (ij) = a_ (ij) -b_ (ij) $ für alle $ i = \\ overline (1, m) $ und $ j = \\ overline (1, n) $.

Erklärung des Eintrags $ i = \\ overline (1, m) $: ein- / ausblenden

Der Eintrag "$ i = \\ overline (1, m) $" bedeutet, dass der Parameter $ i $ von 1 bis m variiert. Beispielsweise besagt der Eintrag $ i = \\ overline (1,5) $, dass der Parameter $ i $ die Werte 1, 2, 3, 4, 5 annimmt.

Es ist anzumerken, dass die Additions- und Subtraktionsoperationen nur für Matrizen derselben Größe definiert sind. Im Allgemeinen sind das Addieren und Subtrahieren von Matrizen Operationen, die intuitiv klar sind, da sie im Wesentlichen nur das Summieren oder Subtrahieren der entsprechenden Elemente bedeuten.

Beispiel №1

Es werden drei Matrizen gegeben:

  $$ A = \\ left (\\ begin (Array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (Array) \\ right) \\; \\; B = \\ left (\\ begin) (Array) (ccc) 10 & ndash; 25 & ndash; 98 \\\\ 3 & ndash; 0 & ndash; 14 (Ende (Array) \\ right); \\; \\; F = \\ left (\\ begin (Array) (cc) 1 & 0 \\\\ -5 & 4 \\ end (Array) \\ right). $$

Ist es möglich, die Matrix $ A + F $ zu finden? Finden Sie Matrizen $ C $ und $ D $, wenn $ C = A + B $ und $ D = A-B $.

Die $ A $ -Matrix enthält 2 Zeilen und 3 Spalten (mit anderen Worten, die Größe der $ A $ -Matrix beträgt $ 2 \\ times 3 $), und die $ F $ -Matrix enthält 2 Zeilen und 2 Spalten. Die Dimensionen der Matrix $ A $ und $ F $ fallen nicht zusammen, daher können wir sie nicht addieren, d.h. Operation $ A + F $ für diese Matrizen ist nicht definiert.

Die Größen der Matrizen $ A $ und $ B $ sind gleich, d.h. Diese Matrizen enthalten die gleiche Anzahl von Zeilen und Spalten, sodass die Additionsoperation auf sie angewendet werden kann.

  $$ C = A + B = \\ left (\\ begin (Array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (Array) \\ right) + \\ left (\\ begin (Array) ) (ccc) 10 & ndash; 25 & ndash; 98 \\\\ 3 & ndash; 0 & ndash; 14 \\ end (array) \\ right) = \\\\ = \\ left (\\ begin (array) (ccc) -1 + 10 & ndash; 2+ ( -25) & 1 + 98 \\\\ 5 + 3 & 9 + 0 & -8 + (- 14) \\ Ende (Array) \\ rechts) = \\ links (\\ Anfang (Array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ Ende (Array) \\ rechts) $$

Finden Sie die Matrix $ D = A-B $:

  $$ D = AB = \\ left (\\ begin (Array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (Array) \\ right) - \\ left (\\ begin (Array) ( ccc) 10 & ndash; 25 & ndash; 98 \\\\ 3 & ndash; 0 & ndash; 14 \\ end (array) \\ right) = \\\\ = \\ left (\\ begin (array) (ccc) -1-10 & ndash; -2 - (- 25 ) & 1-98 \\\\ 5-3 & 9-0 & -8 - (- 14) \\ end (array) \\ right) = \\ left (\\ begin (array) (ccc) -11 & 23 & -97 \\ Die antwort

: $ C = \\ left (\\ begin (Array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (Array) \\ right) $, $ D = \\ left (\\ begin (Array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ Ende (Array) \\ rechts) $.  Matrixmultiplikation mit einer Zahl.

Das Produkt der Matrix $ A_ (m \\ times n) = (a_ (ij)) $ mit der Zahl $ \\ alpha $ ist die Matrix $ B_ (m \\ times n) = (b_ (ij)) $, wobei $ b_ (ij) = \\ alpha \\ cdot a_ (ij) $ für alle $ i = \\ overline (1, m) $ und $ j = \\ overline (1, n) $.

Einfach ausgedrückt bedeutet das Multiplizieren einer Matrix mit einer bestimmten Zahl, dass jedes Element einer gegebenen Matrix mit dieser Zahl multipliziert wird.

Beispiel 2

{!LANG-179998c46e0a688654372913985c9a9b!}

Die Matrix lautet: $ A = \\ left (\\ begin (Array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (Array) \\ right) $. Finden Sie die Matrizen $ 3 \\ cdot A $, $ -5 \\ cdot A $ und $ -A $.

  $$ 3 \\ cdot A = 3 \\ cdot \\ left (\\ begin (Array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (Array) \\ right) = \\ left (\\ begin ( array) (ccc) 3 \\ cdot (-1) & 3 \\ cdot (-2) & 3 \\ cdot 7 \\\\ 3 \\ cdot 4 & 3 \\ cdot 9 & 3 \\ cdot 0 \\ end (array) \\ right) = \\ left (\\ begin (Array) (ccc) -3 & -6 & 21 \\\\ 12 & 27 & 0 \\ end (Array) \\ right). \\\\ -5 \\ cdot A = -5 \\ cdot \\ left (\\ begin (Array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (Array) \\ right) = \\ left (\\ begin (Array) (ccc) -5 \\ cdot (-1) & - 5 \\ cdot (-2) & -5 \\ cdot 7 \\\\ -5 \\ cdot 4 & -5 \\ cdot 9 & -5 \\ cdot 0 \\ end (array) \\ right) = \\ left (\\ begin (array) ( ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ Ende (Array) \\ rechts). $$

Der Eintrag $ -A $ ist ein abgekürzter Eintrag für $ -1 \\ cdot A $. Das heißt, um $ -A $ zu finden, müssen Sie alle Elemente der $ A $ -Matrix mit (-1) multiplizieren. Im Wesentlichen bedeutet dies, dass sich das Vorzeichen aller Elemente der $ A $ -Matrix in das Gegenteil ändert:

  $$ -A = -1 \\ cdot A = -1 \\ cdot \\ left (\\ begin (Array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (Array) \\ right) = \\ : $ 3 \\ cdot A = \\ left (\\ begin (Array) (ccc) -3 & ndash; 6 & ndash; 21 \\\\ 12 & ndash; 27 & ndash; 0 \\ end (Array) \\ right); \\; -5 \\ cdot A = \\ left (\\ begin (Array) (ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ end (Array) \\ right) \\; -A = \\ left (\\ begin (Array) (ccc) 1 & 2 & -7 \\\\ -4 & -9 & 0 \\ end (Array) \\ right) $.

: $ C = \\ left (\\ begin (Array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (Array) \\ right) $, $ D = \\ left (\\ begin (Array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ Ende (Array) \\ rechts) $.  Das Produkt zweier Matrizen.

Die Definition dieser Operation ist umständlich und auf den ersten Blick unverständlich. Daher werde ich zunächst eine allgemeine Definition angeben und dann im Detail analysieren, was dies bedeutet und wie man damit arbeitet.

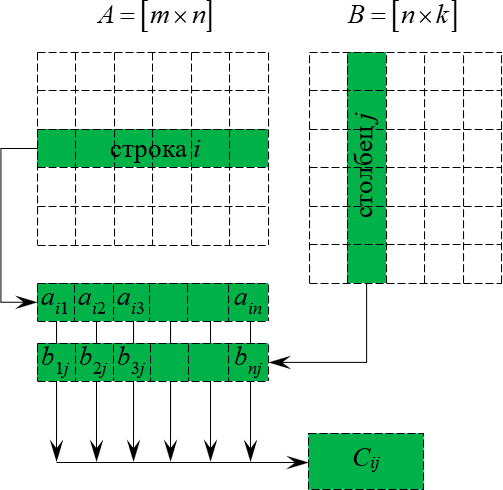
Das Produkt der Matrix $ A_ (m \\ times n) = (a_ (ij)) $ mit der Matrix $ B_ (n \\ times k) = (b_ (ij)) $ ist die Matrix $ C_ (m \\ times k) = (c_ ( ij)) $, wobei jedes Element von $ c_ (ij) $ gleich der Summe der Produkte der entsprechenden Elemente der i-ten Zeile der Matrix $ A $ mit den Elementen der j-ten Spalte der Matrix $ B $ ist: $$ c_ (ij) = \\ sum \\ limits_ (p = 1) ^ (n) a_ (ip) b_ (pj), \\; \\; i = \\ overline (1, m), j = \\ overline (1, n). $$

Die schrittweise Multiplikation von Matrizen wird anhand eines Beispiels erläutert. Sie sollten jedoch sofort beachten, dass nicht alle Matrizen multipliziert werden können. Wenn wir die Matrix $ A $ mit der Matrix $ B $ multiplizieren wollen, müssen wir zuerst sicherstellen, dass die Anzahl der Spalten der Matrix $ A $ gleich der Anzahl der Zeilen der Matrix $ B $ ist (solche Matrizen werden oft genannt)

einverstanden {!LANG-69f0e6da9be87b2fd3d70d6670655bd5!}). Beispielsweise kann die Matrix $ A_ (5 mal 4) $ (die Matrix enthält 5 Zeilen und 4 Spalten) nicht mit der Matrix $ F_ (9 mal 8) $ (9 Zeilen und 8 Spalten) multipliziert werden, da die Anzahl der Spalten der Matrix $ A $ ist nicht gleich der Anzahl der Zeilen der Matrix $ F $, d.h. $ 4 \\ neq 9 $. Es ist jedoch möglich, die Matrix $ A_ (5 mal 4) $ mit der Matrix $ B_ (4 mal 9) $ zu multiplizieren, da die Anzahl der Spalten der Matrix $ A $ gleich der Anzahl der Zeilen der Matrix $ B $ ist. Das Ergebnis der Multiplikation der Matrizen $ A_ (5 \\ times 4) $ und $ B_ (4 \\ times 9) $ ist die Matrix $ C_ (5 \\ times 9) $, die 5 Zeilen und 9 Spalten enthält:

Beispiel 3

Matrizen werden angegeben: $ A = \\ left (\\ begin (array) (cccc) -1 & 2 & -3 & 0 \\\\ 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & -5 \\ end (Array) \\ rechts) $ und $ B = \\ links (\\ begin (Array) (cc) -9 & 3 \\\\ 6 & 20 \\\\ 7 & 0 \\\\ 12 & -4 \\ end (Array) \\ rechts) $. Suchen Sie die Matrix $ C = A \\ cdot B $.

Zunächst bestimmen wir sofort die Größe der Matrix $ C $. Da die Matrix $ A $ eine Größe von $ 3 \\ times 4 $ und die Matrix $ B $ eine Größe von $ 4 \\ times 2 $ hat, ist die Größe der Matrix $ C $ wie folgt: $ 3 \\ times 2 $:

Als Ergebnis des Produkts der Matrizen $ A $ und $ B $ müssen wir also die Matrix $ C $ erhalten, die aus drei Zeilen und zwei Spalten besteht: $ C = \\ left (\\ begin (array) (cc) c_ (11) & c_ ( 12) \\\\ c_ (21) & c_ (22) \\\\ c_ (31) & c_ (32) \\ end (array) \\ right) $. Wenn die Bezeichnungen von Elementen Fragen verursachen, können Sie sich das vorherige Thema ansehen "Matrizen. Arten von Matrizen. Grundbegriffe"  , an deren Anfang die Bezeichnung der Elemente der Matrix erläutert wird. Unser Ziel: die Werte aller Elemente der Matrix $ C $ zu finden.

Beginnen wir mit dem Element $ c_ (11) $. Um das Element $ c_ (11) $ zu erhalten, müssen Sie die Summe der Produkte der Elemente der ersten Zeile der Matrix $ A $ und der ersten Spalte der Matrix $ B $ ermitteln:

Um das Element $ c_ (11) $ selbst zu finden, müssen die Elemente der ersten Zeile der Matrix $ A $ mit den entsprechenden Elementen der ersten Spalte der Matrix $ B $ multipliziert werden, d.h. das erste Element am ersten, das zweite am zweiten, das dritte am dritten, das vierte am vierten. Die Ergebnisse sind zusammengefasst:

  $$ c_ (11) = - 1 \\ cdot (-9) + 2 \\ cdot 6 + (- 3) \\ cdot 7 + 0 \\ cdot 12 = 0. $$

Setzen Sie die Lösung fort und finden Sie $ c_ (12) $. Dazu müssen Sie die Elemente der ersten Zeile der Matrix $ A $ und der zweiten Spalte der Matrix $ B $ multiplizieren:

Ähnlich wie beim Vorgänger haben wir:

  $$ c_ (12) = - 1 \\ cdot 3 + 2 \\ cdot 20 + (- 3) \\ cdot 0 + 0 \\ cdot (-4) = 37. $$

Es werden alle Elemente der ersten Zeile der Matrix $ C $ gefunden. Wir wenden uns der zweiten Zeile zu, in der das Element $ c_ (21) $ beginnt. Um es zu finden, müssen Sie die Elemente der zweiten Zeile der Matrix $ A $ und der ersten Spalte der Matrix $ B $ multiplizieren:

  $$ c_ (21) = 5 \\ cdot (-9) + 4 \\ cdot 6 + (-2) \\ cdot 7 + 1 \\ cdot 12 = -23. $$

Das nächste Element $ c_ (22) $ wird gefunden, indem die Elemente der zweiten Zeile der Matrix $ A $ mit den entsprechenden Elementen der zweiten Spalte der Matrix $ B $ multipliziert werden:

  $$ c_ (22) = 5 \\ cdot 3 + 4 \\ cdot 20 + (- 2) \\ cdot 0 + 1 \\ cdot (-4) = 91. $$

Um $ c_ (31) $ zu finden, multiplizieren Sie die Elemente der dritten Zeile der Matrix $ A $ mit den Elementen der ersten Spalte der Matrix $ B $:

  $$ c_ (31) = - 8 \\ cdot (-9) + 11 \\ cdot 6 + (- 10) \\ cdot 7 + (-5) \\ cdot 12 = 8. $$

Und um schließlich das Element $ c_ (32) $ zu finden, müssen wir die Elemente der dritten Zeile der Matrix $ A $ mit den entsprechenden Elementen der zweiten Spalte der Matrix $ B $ multiplizieren:

  $$ c_ (32) = - 8 \\ cdot 3 + 11 \\ cdot 20 + (- 10) \\ cdot 0 + (-5) \\ cdot (-4) = 216. $$

Alle Elemente der Matrix $ C $ werden gefunden, es bleibt nur aufzuzeichnen, dass $ C = \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right) $ . Oder wenn Sie bereits vollständig geschrieben haben:

  $$ C = A \\ cdot B = \\ left (\\ begin (Array) (cccc) -1 & 2 & -3 & 0 \\\\ 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & - 5 \\ end (array) \\ right) \\ cdot \\ left (\\ begin (array) (cc) -9 & 3 \\\\ 6 & 20 \\\\ 7 & 0 \\\\ 12 & -4 \\ end (array) \\ right) = \\ left (\\ begin (Array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (Array) \\ right). $$

: $ C = \\ left (\\ begin (Array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (Array) \\ right) $, $ D = \\ left (\\ begin (Array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ Ende (Array) \\ rechts) $.: $ C = \\ left (\\ begin (Array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (Array) \\ right) $.

Im Übrigen gibt es oft keinen Grund, das Finden jedes Elements der Ergebnismatrix im Detail zu beschreiben. Für Matrizen, deren Größe klein ist, können Sie dies tun:

Es ist auch erwähnenswert, dass die Multiplikation von Matrizen nicht kommutativ ist. Dies bedeutet, dass im allgemeinen Fall $ A \\ cdot B \\ neq B \\ cdot A $. Nur für einige Arten von Matrizen, die aufgerufen werden durchlässig  (oder Pendeln) ist die Gleichheit $ A \\ cdot B = B \\ cdot A $ wahr. Basierend auf der Nichtkommutativität der Multiplikation muss angegeben werden, wie genau wir den Ausdruck mit der einen oder anderen Matrix multiplizieren: rechts oder links. Beispielsweise bedeutet der Ausdruck "beide Seiten der Gleichheit $ 3E-F = Y $ mit der Matrix $ A $ auf der rechten Seite multiplizieren", dass wir die folgende Gleichheit erhalten müssen: $ (3E-F) \\ cdot A = Y \\ cdot A $.

In Bezug auf die Matrix $ A_ (m \\ times n) = (a_ (ij)) $ wird die Matrix $ A_ (n \\ times m) ^ (T) = (a_ (ij) ^ (T)) $ für Elemente genannt welches $ a_ (ij) ^ (T) = a_ (ji) $.

Einfach ausgedrückt, um die transponierte Matrix $ A ^ T $ zu erhalten, müssen Sie die Spalten in der ursprünglichen Matrix $ A $ nach diesem Prinzip durch die entsprechenden Zeilen ersetzen: Wenn die erste Zeile wäre, wäre die erste Spalte; war die zweite Reihe - wird die zweite Spalte werden; Es gab eine dritte Reihe - es würde eine dritte Spalte geben und so weiter. Suchen wir zum Beispiel eine transponierte Matrix für die $ A_ (3 \\ times 5) $ -Matrix:

Wenn also die ursprüngliche Matrix eine Größe von 3 mal 5 Dollar hatte, dann hat die transponierte Matrix eine Größe von 5 mal 3 Dollar.

  Einige Eigenschaften von Operationen auf Matrizen.

Hier wird angenommen, dass $ \\ alpha $, $ \\ beta $ einige Zahlen sind und $ A $, $ B $, $ C $ Matrizen sind. Für die ersten vier Eigenschaften habe ich die Namen angegeben, der Rest kann analog zu den ersten vier aufgerufen werden.

1. $ A + B = B + A $ (Additionskommutativität)
2. $ A + (B + C) = (A + B) + C $ (Additionsassoziativität)
3. $ (\\ alpha + \\ beta) \\ cdot A = \\ alpha A + \\ beta A $ (Verteilbarkeit der Multiplikation mit einer Matrix bezüglich der Addition von Zahlen)
4. $ \\ alpha \\ cdot (A + B) = \\ alpha A + \\ alpha B $ (Verteilbarkeit der Multiplikation mit der Zahl bezüglich der Addition von Matrizen)
5. $ A (BC) = (AB) C $
6. $ (\\ alpha \\ beta) A = \\ alpha (\\ beta A) $
7. $ A \\ cDot (B + C) = AB + AC $, $ (B + C) \\ cDot A = BA + CA $.
8. $ A \\ cdot E = A $, $ E \\ cdot A = A $, wobei $ E $ die Identitätsmatrix der entsprechenden Bestellung ist.
9. $ A \\ cdot O = O $, $ O \\ cdot A = O $, wobei $ O $ die Nullmatrix der entsprechenden Größe ist.
10. $ \\ left (A ^ T \\ right) ^ T = A $
11. $ (A + B) ^ T = A ^ T + B ^ T $
12. $ (AB) ^ T = B ^ T \\ cdot A ^ T $
13. $ \\ left (\\ alpha A \\ right) ^ T = \\ alpha A ^ T $

Im nächsten Teil werden wir die Operation zum Erhöhen der Matrix auf einen nichtnegativen ganzzahligen Grad betrachten und auch Beispiele lösen, in denen mehrere Operationen an Matrizen erforderlich sind.