Berechnen Sie die Determinante des Produkts zweier Matrizen. Determinante des Produkts von Matrizen. Determinante des Produkts zweier quadratischer Matrizen

Vorlesung 6

4.6 Determinante des Produkts zweier quadratischer Matrizen.

Produkt zweier quadratischer Matrizen N Die -te Ordnung ist immer definiert. In diesem Fall ist der folgende Satz wichtig.

Satz. Die Determinante des Matrixprodukts ist gleich dem Produkt der Determinanten der Faktormatrizen:

Nachweisen. Lassen

Und
,

.

Lassen Sie uns eine Hilfsdeterminante erstellen

.

Als Folge des Satzes von Laplace gilt:

.

Also,
, das werden wir zeigen
. Dazu transformieren wir die Determinante wie folgt. Die Ersten zuerst P
, Hinzufügen zu
-te Spalte. Dann der Erste P Spalten multipliziert mit
, Hinzufügen zu
-te Spalte usw. Im letzten Schritt zu
Die erste Spalte wird hinzugefügt P Spalten multipliziert mit
. Als Ergebnis erhalten wir die Determinante

.

Erweitern der resultierenden Determinante unter Verwendung des Satzes von Laplace in Bezug auf den letzten P Spalten finden wir:

Die Gleichheiten sind also bewiesen
Und
, woraus folgt
.

4.7.Inverse Matrix

Definition 1 . Gegeben sei eine quadratische Matrix A P-te Ordnung. Quadratische Matrix
der gleichen Ordnung werden aufgerufen umkehren zur Matrix A, wenn , wo E-Identitätsmatrix P-te Ordnung.

Stellungnahme. Wenn es eine Matrixinverse der Matrix gibt A, dann ist eine solche Matrix eindeutig.

Nachweisen. Nehmen wir an, dass die Matrix
ist nicht die einzige Matrixinverse der Matrix A. Nehmen wir eine weitere inverse Matrix B. Dann sind die Bedingungen erfüllt

Schauen wir uns die Arbeit an
. Für ihn gibt es Gleichberechtigung

woraus folgt
. Damit ist die Eindeutigkeit der inversen Matrix bewiesen.

Um den Satz über die Existenz einer inversen Matrix zu beweisen, benötigen wir das Konzept der „adjungierten Matrix“.

Definition 2 . Die Matrix sei gegeben

.

deren Elemente algebraische Komplemente sind Elemente Matrizen A, angerufen beigefügt Matrix zu Matrix A.

Achten wir darauf, dass wir die adjungierte Matrix konstruieren MIT Matrixelemente A Sie müssen sie durch algebraische Additionen ersetzen und dann die resultierende Matrix transponieren.

Definition 3. Quadratische Matrix A angerufen nicht entartet , Wenn
.

Satz. Damit die Matrix A hatte eine inverse Matrix
, ist es notwendig und ausreichend, dass die Matrix A war nicht entartet. In diesem Fall die Matrix
wird durch die Formel bestimmt

, (1)

Wo - algebraische Additionen von Matrixelementen A.

Nachweisen. Lassen Sie die Matrix A hat eine inverse Matrix
. Dann sind die Bedingungen, aus denen es folgt, erfüllt. Aus der letzten Gleichung erhalten wir die Determinanten
Und
. Diese Determinanten sind durch die Relation miteinander verbunden
. Matrizen A Und
nicht entartet, weil ihre Determinanten ungleich Null sind.

Lassen Sie uns nun die Matrix A nicht entartet. Beweisen wir, dass die Matrix A hat eine inverse Matrix
und es wird durch Formel (1) bestimmt. Schauen wir uns dazu die Arbeit an

Matrizen A und die damit verbundene Matrix MIT.

Gemäß der Matrixmultiplikationsregel ist das Element funktioniert
Matrizen A Und MIT hat die Form: . Da die Summe der Produkte von Elementen ich te Zeilen zu algebraischen Komplementen der entsprechenden Elemente J- Die Zeile ist gleich Null bei
und die Determinante bei
. Somit,

Wo E- Identitätsmatrix P-te Ordnung. Die Gleichheit wird auf ähnliche Weise bewiesen
. Auf diese Weise,

, was bedeutet, dass
und Matrix ist die Umkehrung der Matrix A. Daher die nicht singuläre Matrix A hat eine inverse Matrix, die durch Formel (1) bestimmt wird.

Folgerung 1 . Matrixdeterminanten A Und
durch die Relation verbunden
.

Folgerung 2 . Haupteigenschaft der adjungierten Matrix MIT zur Matrix A ausgedrückt wird

Gleichheiten
.

Folgerung 3 . Determinante einer nicht singulären Matrix A und die damit verbundene Matrix

MIT der Gleichheit verpflichtet
.

Folgerung 3 folgt aus der Gleichheit
und Eigenschaften von Determinanten, nach denen bei Multiplikation mit P- Potenz dieser Zahl. In diesem Fall

woraus folgt das
.

Beispiel. A:

.

Lösung. Matrixdeterminante

verschieden von Null. Daher die Matrix A hat das Gegenteil. Um es zu finden, berechnen wir zunächst die algebraischen Komplemente:

,
,
,

,
,
,

,
.

Nun schreiben wir mit Formel (1) die inverse Matrix

.

4.8. Elementare Transformationen über Matrizen. Gauß-Algorithmus.

Definition 1. Unter elementare Transformationen über der Größenmatrix

Verstehen Sie die folgenden Schritte.

Multiplizieren einer beliebigen Zeile (Spalte) einer Matrix mit einer beliebigen Zahl ungleich Null.

Zu jedem hinzufügen ich te Zeile der Matrix einer ihrer J- String multipliziert mit einer beliebigen Zahl.

Zu jedem hinzufügen ich die te Spalte der Matrix einer ihrer J- Spalte mit einer beliebigen Zahl multipliziert.

Neuanordnen der Zeilen (Spalten) einer Matrix.

Definition 2. Matrizen A Und IN wir rufen an Äquivalent , wenn einer von ihnen durch elementare Transformationen in einen anderen umgewandelt werden kann. Werde schreiben
.

Die Matrixäquivalenz hat die folgenden Eigenschaften:

Definition 3 . Geschritten wird als Matrix bezeichnet A mit folgenden Eigenschaften:

1) wenn ich-te Zeile ist Null, d.h. besteht also nur aus Nullen
-te Zeile ist ebenfalls Null;

2) wenn die ersten Nicht-Null-Elemente ich und
Die Zeilen befinden sich in Spalten mit Zahlen k Und l, Das
.

Beispiel. Matrizen

Und

sind schrittweise und die Matrix

ist nicht gestuft.

Lassen Sie uns zeigen, wie wir mithilfe elementarer Transformationen die Matrix reduzieren können A zu einer Stufenansicht.

Gaußscher Algorithmus . Betrachten Sie die Matrix A Größe
. Ohne Beschränkung der Allgemeinheit können wir davon ausgehen
. (Wenn in der Matrix A Wenn es mindestens ein Element ungleich Null gibt, können wir durch Neuanordnen der Zeilen und dann der Spalten sicherstellen, dass dieses Element am Schnittpunkt der ersten Zeile und der ersten Spalte liegt.) Zur zweiten Zeile der Matrix hinzufügen A zuerst multipliziert mit , bis zur dritten Zeile – der ersten, multipliziert mit usw.

Als Ergebnis bekommen wir das

.

Elemente in der neuesten
Linien werden durch die Formeln bestimmt:

,
,
.

Betrachten Sie die Matrix

.

Wenn alle Matrixelemente sind dann gleich Null

und die äquivalente Matrix ist schrittweise. Wenn unter den Matrixelementen mindestens eins von Null verschieden ist, dann können wir das ohne Beschränkung der Allgemeinheit annehmen
(Dies kann durch Neuanordnen der Zeilen und Spalten der Matrix erreicht werden ). In diesem Fall wird die Matrix transformiert genau wie eine Matrix A, wir bekommen

jeweils,

.

Hier
,
,
.

Und
,
, … ,
. In der Matrix A T Linien zu zeichnen und sie auf die angegebene Weise schrittweise in Form zu bringen, mehr brauchen Sie nicht T Schritte. Dann kann der Prozess um enden k-ter Schritt genau dann, wenn alle Elemente der Matrix

sind gleich Null. In diesem Fall

Und
,
, … ,
.

4.9. Finden der inversen Matrix mithilfe elementarer Transformationen.

Für eine große Matrix ist es praktisch, die inverse Matrix mithilfe elementarer Transformationen auf Matrizen zu finden. Diese Methode ist wie folgt. Schreiben Sie die zusammengesetzte Matrix auf
und gemäß dem Gaußschen Methodenschema werden sie in den Zeilen dieser Matrix (d. h. gleichzeitig in der Matrix) durchgeführt A und in der Matrix E) elementare Transformationen. Als Ergebnis die Matrix A wird in die Identitätsmatrix und die Matrix umgewandelt E– in die Matrix
.

Beispiel. Finden Sie die Matrixinverse einer Matrix

.

Lösung. Schreiben wir die zusammengesetzte Matrix
und transformieren Sie es mithilfe elementarer Stringtransformationen gemäß der Gaußschen Methode. Als Ergebnis erhalten wir:

.

Aus diesen Transformationen schließen wir das

.

4.10 Matrixrang.

Definition. Ganze Zahl R angerufen Rang Matrizen A, wenn es sich um eine Nebenbestellung handelt R, ungleich Null, und alle Minderjährigen haben eine höhere Ordnung R sind gleich Null. Der Rang der Matrix wird durch das Symbol angegeben
.

Der Rang der Matrix wird mit der Methode berechnet angrenzende Minderjährige .

Beispiel. Berechnen Sie den Rang der Matrix mithilfe der Methode der angrenzenden Minderjährigen

.

Lösung.

Die obige Methode ist nicht immer praktisch, weil... verbunden mit der Berechnung von groß

Anzahl der Determinanten.

Stellungnahme. Der Rang einer Matrix ändert sich bei elementaren Transformationen ihrer Zeilen und Spalten nicht.

Die angegebene Aussage gibt die zweite Möglichkeit an, den Rang einer Matrix zu berechnen. Es wird genannt nach der Methode der Elementartransformationen . Um den Rang einer Matrix zu ermitteln, müssen Sie die Gaußsche Methode verwenden, um sie auf eine schrittweise Form zu reduzieren, und dann den maximalen Mollwert ungleich Null auswählen. Lassen Sie uns dies anhand eines Beispiels erklären.

Beispiel. Berechnen Sie mithilfe elementarer Transformationen den Rang der Matrix

.

Lösung. Führen wir eine Kette elementarer Transformationen nach der Gaußschen Methode durch. Als Ergebnis erhalten wir eine Kette äquivalenter Matrizen.

Definition. Produkt zweier Matrizen A Und IN wird als Matrix bezeichnet MIT, dessen Element sich an der Kreuzung befindet ich te Linie und J Spalte, gleich der Summe der Produkte der Elemente ich Zeile der Matrix A zu den entsprechenden (in der Reihenfolge) Elementen J te Matrixspalte IN.

Aus dieser Definition folgt die Matrixelementformel C:

Matrixprodukt A zur Matrix IN bezeichnet durch AB.

Beispiel 1. Finden Sie das Produkt zweier Matrizen A Und B, Wenn

,

.

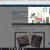
Lösung. Es ist praktisch, das Produkt zweier Matrizen zu finden A Und IN Schreiben Sie wie in Abb. 2:

Im Diagramm zeigen graue Pfeile an, welche Zeilen der Matrix Elemente sind A zu den Elementen welcher Spalte der Matrix IN müssen multipliziert werden, um Matrixelemente zu erhalten MIT, und die Linien sind die Farben des Matrixelements C die entsprechenden Matrixelemente sind verbunden A Und B, deren Produkte addiert werden, um ein Matrixelement zu erhalten C.

Als Ergebnis erhalten wir die Elemente des Matrixprodukts:

Jetzt haben wir alles, um das Produkt zweier Matrizen aufzuschreiben:

.

Produkt zweier Matrizen AB macht nur Sinn, wenn die Anzahl der Matrixspalten A stimmt mit der Anzahl der Matrixzeilen überein IN.

Diese wichtige Funktion können Sie sich leichter merken, wenn Sie die folgenden Erinnerungen häufiger verwenden:

Es gibt noch ein weiteres wichtiges Merkmal des Matrizenprodukts in Bezug auf die Anzahl der Zeilen und Spalten:

Im Produkt von Matrizen AB Die Anzahl der Zeilen ist gleich der Anzahl der Zeilen der Matrix A, und die Anzahl der Spalten ist gleich der Anzahl der Matrixspalten IN .

Beispiel 2. Ermitteln Sie die Anzahl der Zeilen und Spalten einer Matrix C, das das Produkt zweier Matrizen ist A Und B folgende Abmessungen:

a) 2 x 10 und 10 x 5;

b) 10 x 2 und 2 x 5;

Beispiel 3. Finden Sie das Produkt von Matrizen A Und B, Wenn:

.

A B- 2. Daher die Dimension der Matrix C = AB- 2 x 2.

Berechnung von Matrixelementen C = AB.

Das gefundene Produkt von Matrizen: .

Die Lösung für dieses und andere ähnliche Probleme finden Sie unter Online-Matrixproduktrechner .

Beispiel 5. Finden Sie das Produkt von Matrizen A Und B, Wenn:

.

Lösung. Anzahl der Zeilen in der Matrix A- 2, Anzahl der Spalten in der Matrix B C = AB- 2 x 1.

Berechnung von Matrixelementen C = AB.

Das Produkt der Matrizen wird als Spaltenmatrix geschrieben: .

Die Lösung für dieses und andere ähnliche Probleme finden Sie unter Online-Matrixproduktrechner .

Beispiel 6. Finden Sie das Produkt von Matrizen A Und B, Wenn:

.

Lösung. Anzahl der Zeilen in der Matrix A- 3, Anzahl der Spalten in der Matrix B- 3. Daher die Dimension der Matrix C = AB- 3 x 3.

Berechnung von Matrixelementen C = AB.

Das gefundene Produkt von Matrizen: .

Die Lösung für dieses und andere ähnliche Probleme finden Sie unter Online-Matrixproduktrechner .

Beispiel 7. Finden Sie das Produkt von Matrizen A Und B, Wenn:

.

Lösung. Anzahl der Zeilen in der Matrix A- 1, Anzahl der Spalten in der Matrix B- 1. Daher die Dimension der Matrix C = AB- 1 x 1.

Berechnung des Matrixelements C = AB.

Das Produkt von Matrizen ist eine Matrix aus einem Element: .

Die Lösung für dieses und andere ähnliche Probleme finden Sie unter Online-Matrixproduktrechner .

Die Softwareimplementierung des Produkts zweier Matrizen in C++ wird im entsprechenden Artikel im Block „Computer und Programmierung“ besprochen.

Matrixpotenzierung

Unter Potenzierung einer Matrix versteht man die Multiplikation einer Matrix mit derselben Matrix. Da ein Produkt von Matrizen nur existiert, wenn die Anzahl der Spalten der ersten Matrix mit der Anzahl der Zeilen der zweiten Matrix übereinstimmt, können nur quadratische Matrizen potenziert werden. N Potenz einer Matrix durch Multiplikation der Matrix mit sich selbst N einmal:

Beispiel 8. Gegeben sei eine Matrix. Finden A² und A³ .

Finden Sie selbst das Matrixprodukt und schauen Sie sich dann die Lösung an

Beispiel 9. Gegeben sei eine Matrix

Finden Sie das Produkt der gegebenen Matrix und der transponierten Matrix, das Produkt der transponierten Matrix und der gegebenen Matrix.

Eigenschaften des Produkts zweier Matrizen

Eigentum 1. Das Produkt einer beliebigen Matrix A und der Identitätsmatrix E der entsprechenden Ordnung, sowohl rechts als auch links, stimmt mit der Matrix A überein, d.h. AE = EA = A.

Mit anderen Worten: Die Rolle der Einheitsmatrix bei der Matrixmultiplikation ist dieselbe wie die Rolle der Einheiten bei der Zahlenmultiplikation.

Beispiel 10.Überprüfen Sie, ob Eigenschaft 1 wahr ist, indem Sie die Matrixprodukte ermitteln

zur Identitätsmatrix rechts und links.

Lösung. Da die Matrix A drei Spalten enthält, müssen Sie das Produkt finden AE, Wo

-
Identitätsmatrix dritter Ordnung. Lassen Sie uns die Elemente der Arbeit finden MIT = AE :

Es stellt sich heraus, dass AE = A .

Lassen Sie uns nun das Produkt finden EA, Wo E ist eine Identitätsmatrix zweiter Ordnung, da Matrix A zwei Zeilen enthält. Lassen Sie uns die Elemente der Arbeit finden MIT = EA :

Satz. Seien A und B zwei quadratische Matrizen der Ordnung n. Dann ist die Determinante ihres Produkts gleich dem Produkt der Determinanten, d.h.

| AB | = | A| | B|.

¢ Sei A = (a ij) n x n , B = (b ij) n x n . Betrachten Sie die Determinante d 2 n der Ordnung 2n

d2n = | A | | B | (-1) 1 + ... + n + 1 + ... + n = | A | | B|.

Wenn wir zeigen, dass die Determinante von d 2 n gleich der Determinante der Matrix C=AB ist, dann ist der Satz bewiesen.

In d 2 n werden wir die folgenden Transformationen durchführen: Zu 1 Zeile addieren wir (n+1) Zeile multipliziert mit a 11; (n+2) Zeichenfolge multipliziert mit einer 12 usw. (2n) String multipliziert mit a 1 n . In der resultierenden Determinante sind die ersten n Elemente der ersten Zeile Nullen und die anderen n Elemente sehen folgendermaßen aus:

a 11 b 11 + a 12 b 21 + ... + a 1n b n1 = c 11;

a 11 b 12 + a 12 b 22 + ... + a 1n b n2 = c 12;

a 11 b 1n + a 12 b 2n + ... + a 1n b nn = c 1n.

In ähnlicher Weise erhalten wir Nullen in 2, ..., n Zeilen der Determinante d 2 n, und die letzten n Elemente in jeder dieser Zeilen werden zu den entsprechenden Elementen der Matrix C. Als Ergebnis beträgt die Determinante d 2 n in eine gleichwertige Determinante umgewandelt:

d2n = | C | (-1) 1 + ... + n + ... + 2n = |AB|. £

Folge. Die Determinante des Produkts einer endlichen Anzahl quadratischer Matrizen ist gleich dem Produkt ihrer Determinanten.

¢ Der Beweis erfolgt durch Induktion: | A 1 ... A i +1 | = | A 1 ... A i | | A i +1 | = ... = = | A 1 | ... | A i +1 | . Diese Gleichungskette ist nach dem Satz richtig. £

Inverse Matrix.

Sei A = (a ij) n x n eine quadratische Matrix über dem Körper P.

Definition 1. Matrix A heißt singulär, wenn ihre Determinante gleich 0 ist. Andernfalls heißt Matrix A nicht singulär.

Definition 2. Sei A Î P n . Wir nennen die Matrix B Î P n invers zu A, wenn AB = BA=E.

Satz (Matrixinvertibilitätskriterium). Eine Matrix A ist genau dann invertierbar, wenn sie nicht singulär ist.

¢ Es sei A eine inverse Matrix. Dann ist AA -1 = E und unter Anwendung des Satzes über die Multiplikation von Determinanten erhalten wir | A | | A -1 | = | E | oder | A | | A -1 | = 1. Daher ist | A | Nr. 0.

Lass, zurück, | A | ¹ 0. Es muss gezeigt werden, dass es eine Matrix B gibt, so dass AB = BA = E. Als B nehmen wir die folgende Matrix:

wobei A ij das algebraische Komplement zum Element a ij ist. Dann

Es ist zu beachten, dass das Ergebnis eine Identitätsmatrix sein wird (es reicht aus, die Korollare 1 und 2 aus dem Laplace-Theorem § 6 zu verwenden), d. h. AB = E. Ebenso wird gezeigt, dass BA = E. £

Beispiel. Finden Sie für Matrix A die inverse Matrix oder beweisen Sie, dass sie nicht existiert.

det A = -3 inverse Matrix existiert. Jetzt berechnen wir die algebraischen Additionen.

A 11 = -3 A 21 = 0 A 31 = 6

A 12 = 0 A 22 = 0 A 32 = -3

A 13 = 1 A 23 = -1 A 33 = -1

Die inverse Matrix sieht also wie folgt aus: B = =

Algorithmus zum Finden der inversen Matrix für Matrix A.

1. Berechnen Sie det A.

2. Wenn es 0 ist, existiert die inverse Matrix nicht. Wenn det A ungleich 0 ist, berechnen wir algebraische Additionen.

3. Wir setzen algebraische Zusätze an den entsprechenden Stellen ein.

4. Teilen Sie alle Elemente der resultierenden Matrix durch det A.

Übung 1. Finden Sie heraus, ob die inverse Matrix eindeutig ist.

Übung 2. Die Elemente der Matrix A seien rationale ganze Zahlen. Werden die Elemente der inversen Matrix rationale ganze Zahlen sein?

Systeme linearer Gleichungen.

Definition 1. Eine Gleichung der Form a 1 x 1 + ....+a n x n =b, wobei a, ...,a n Zahlen sind; x 1 , ... , x n - Unbekannte, sogenannte lineare Gleichung mit N Unbekannt.

S Gleichungen mit N Unbekannte nennt man ein System S lineare Gleichungen mit N unbekannt, d.h.

Matrix A, bestehend aus Koeffizienten für die Unbekannten von System (1), wird als Matrix von System (1) bezeichnet.

.

Wenn wir der Matrix A eine Spalte mit freien Termen hinzufügen, erhalten wir eine erweiterte Matrix des Systems (1).

X = - Spalte der Unbekannten.

Kolumne der freien Mitglieder.

In Matrixform sieht das System wie folgt aus: AX=B (2).

Eine Lösung für System (1) ist eine geordnete Menge N Zahlen (α 1 ,…, α n), so dass wir numerische Identitäten erhalten, wenn wir in (1) x 1 = α 1 , x 2 = α 2 ,…, x n = α n ersetzen.

Definition 2. System (1) heißt konsistent, wenn es Lösungen hat, andernfalls inkonsistent.

Definition 3. Zwei Systeme heißen äquivalent, wenn ihre Lösungsmengen übereinstimmen.

Es gibt einen universellen Weg, System (1) zu lösen – die Gauß-Methode (Methode der sequentiellen Eliminierung von Unbekannten), siehe Seite 15.

Betrachten wir den Fall genauer s = n. Zur Lösung solcher Systeme gibt es die Cramer-Methode.

Sei d = det,

d j ist die Determinante von d, in der die j-te Spalte durch eine Spalte mit freien Termen ersetzt wird.

Satz (Cramer-Regel). Wenn die Determinante des Systems d ¹ 0 ist, dann hat das System eine eindeutige Lösung, die durch die Formeln erhalten wird:

x 1 = d 1 / d …x n = d n / d

¢Die Idee des Beweises besteht darin, System (1) in Form einer Matrixgleichung umzuschreiben. Lasst uns

und betrachten Sie die Gleichung AX = B (2) mit einer unbekannten Spaltenmatrix X. Da A, X, B Größenmatrizen sind n x n, n x 1, n x 1 Dementsprechend ist das Produkt rechteckiger Matrizen AX definiert und hat die gleichen Abmessungen wie die Matrix B. Daher ist Gleichung (2) sinnvoll.

Der Zusammenhang zwischen System (1) und Gleichung (2) besteht darin, was die Lösung eines gegebenen Systems genau dann ist, wenn

Die Spalte ist die Lösung von Gleichung (2).

Tatsächlich bedeutet diese Aussage die Gleichheit

=

Als ,

wobei A ij das algebraische Komplement des Elements a ij in der Determinante d ist

= ,

von wo (4).

In Gleichung (4) ist in Klammern die Entwicklung in Elemente der j-ten Spalte der Determinante d j geschrieben, die aus der Determinante d nach ihrer Ersetzung erhalten wird

Die j-te Spalte ist die Spalte der freien Begriffe. Deshalb, x j = d j / d.£

Folge. Liegt ein homogenes System von n linearen Gleichungen vor N der Unbekannten eine Lösung ungleich Null hat, dann ist die Determinante dieses Systems gleich Null.

THEMA 3. Polynome in einer Variablen.

Bezeichnet wird die Determinante einer Matrix. Mit anderen Worten: Die Determinante einer Matrix ist die Summe der Produkte aus der Menge multipliziert mit dem Vorzeichen der entsprechenden Substitution.

Die Determinante zweiter Ordnung ist gleich dem Produkt der Elemente der Hauptdiagonale abzüglich des Produkts der Elemente auf der Seitendiagonale.

Wir haben die Dreiecksregel:

Die einfachsten Eigenschaften von Determinanten

Die Determinante einer Matrix mit einer Nullzeile (Spalte) ist gleich Null

Die Determinante einer Dreiecksmatrix ist gleich dem Produkt der auf der Hauptdiagonalen liegenden Elemente

Es handelt sich um eine Dreiecksmatrix, wenn die Elemente unter der Hauptdiagonale Null sind.

Die Determinante einer Diagonalmatrix ist gleich dem Produkt der auf der Hauptdiagonalen liegenden Elemente. Eine Matrix ist diagonal, wenn alle außerhalb der Hauptdiagonalen liegenden Elemente Null sind.

Grundlegende Eigenschaften von Determinanten

Feld der Skalare,

Nachweisen:

bezeichnen wir Wenn es die gesamte Menge „durchläuft“, dann „durchläuft“ es auch alles, d. h.

Wenn zwei Spalten (Zeilen) einer Matrix neu angeordnet werden, ändert sich das Vorzeichen ihrer Determinante.

Nachweisen:

I) Spalten neu anordnen:

Sei eine Matrix, die durch Neuanordnen zweier Spalten mit Zahlen erhalten wird, wo. Betrachten wir die Umsetzung:

Transposition ist eine seltsame Substitution,

Im Beweis verwenden wir die Gleichung:

Wenn es die gesamte Wertemenge durchläuft, dann durchläuft es auch alle Werte und

II) Saitenumordnung

Lassen Sie es aus einer Permutation von zwei Zeilen und dann aus einer Permutation von zwei Spalten erhalten werden

III) Determinante einer Matrix mit zwei identischen Zeilen (Spalten) gleich Null

Nachweisen:

Lassen Sie uns für ein solches Feld durchführen, wo

Kommentar

Den Beweis für diesen Fall finden Sie in Kulikovas Lehrbuch Algebra und Zahlentheorie

Es gebe zwei identische Zeilen mit Zahlen, und wenn wir die Zeilen vertauschen, erhalten wir eine Matrix

Wenn es zwei identische Spalten gibt, dann hat die transponierte Matrix zwei identische Zeilen

IV) Wenn alle Elemente einer beliebigen Zeile (Spalte) der Matrix mit multipliziert werden, wird die Determinante mit multipliziert

Nachweisen:

Lassen Sie es durch Multiplikation mit Zeilen erhalten

seit damals

Ähnlicher Beweis für Spalten

V) Determinante einer Matrix, deren zwei Zeilen (Spalten) proportional zu Null sind

Nachweisen:

Die Zeilen in der Matrix seien proportional, d.h. -string ist gleich dem Produkt von -string. Lassen

Für Spalten:

Es sei erhalten aus, . Die Spalten sind sowohl proportional als auch

VI) Wenn jedes Element einer Zeile (Spalte) einer quadratischen Matrix die Summe zweier Elemente ist, dann ist die Determinante gleich der Summe der beiden Determinanten. In der Matrix der ersten Determinante werden in der Zeile (Spalte) die ersten Terme und in der Matrix der zweiten Determinante die zweiten Terme geschrieben. Die übrigen Elemente der Matrizen dieser Determinanten sind dieselben wie die der Matrix

Nachweisen:

VII) Wenn Sie einer beliebigen Zeile (Spalte) der Matrix der Determinante eine weitere Zeile (Spalte) multipliziert mit hinzufügen, ändert sich die Determinante nicht.

Nachweisen:

Das Gleiche gilt für Spalten.

VIII) Wenn eine Zeile (Spalte) der Matrix eine lineare Kombination anderer Zeilen (Spalten) ist, dann ist die Determinante

Nachweisen:

Wenn eine Zeichenfolge eine lineare Kombination anderer Zeichenfolgen ist, können weitere Zeichenfolgen hinzugefügt und mit Skalaren multipliziert werden, sodass eine Nullzeichenfolge erhalten wird. Die Determinante einer solchen Matrix ist gleich Null.

(Multiplizieren Sie zuerst die erste Zeile mit -2 und addieren Sie mit der zweiten, dann mit -3 und addieren Sie mit der dritten). Diese Regel der Reduktion auf Dreiecksform wird für Ordnungsdeterminanten verwendet:

da die Determinante einer Dreiecksmatrix gleich dem Produkt der auf der Hauptdiagonalen liegenden Elemente ist.

Wenn eine quadratische Matrix das Produkt einiger Matrizen (die rechteckig sein können) ist, ist es oft wichtig, die Determinante des Produkts durch die Eigenschaften der Faktoren ausdrücken zu können. Der folgende Satz ist ein aussagekräftiger Indikator dafür.

Nebensätze und algebraische Komplemente.

Determinantensätze.

Feld der Skalare,

Def. Das untergeordnete Element der Ordnungsdeterminante ist die Ordnungsdeterminante, die man durch Streichen der -Zeile und -Spalte erhält.

Hauptminderjährige der Determinante

Es gibt Qualifikationen für Haupt- und Nebenfächer

Betrachten Sie die Matrix und berechnen Sie ihre Nebenwerte

Definition. Das algebraische Komplement eines Elements ist eine Zahl

Beispiel: Berechnen wir,

Nachweisen:

(In der Summe sind nur die Terme ungleich Null, wobei)

Dann hat die Substitution die Form: , wo. Lassen Sie uns die Substitution anpassen, d. h.

Eine solche Entsprechung wird als Eins-zu-Eins-Abbildung von der Menge der Permutationen auf die Menge der Permutationen bezeichnet. Offensichtlich haben sie die gleichen Inversionen, was bedeutet, dass sie die gleiche Parität und das gleiche Vorzeichen haben

Wenn alle Elemente einer beliebigen Zeile (Spalte) einer Matrix mit der möglichen Ausnahme eines Elements gleich Null sind, dann ist die Determinante der Matrix gleich dem Produkt dieses Elements und seines algebraischen Komplements

Nachweisen:

Alle Elemente außer dem Element seien Zeilen der Matrix

Durch die Neuanordnung von Zeilen und Spalten haben wir das Element in die untere rechte Ecke verschoben, was Zeilen und Spalten bedeutet. Das Vorzeichen ändert sich einmal, woraufhin das Ergebnis eine Matrix ist, in der alle Elemente der letzten Zeile außer möglicherweise gleich Null sind. Nach Lemma 1, weil

Satz von Lagrange

ist gleich der Summe der Produkte der Elemente einer beliebigen Spalte (Zeile) der Matrix und ihrem algebraischen Komplement. Mit anderen Worten: Die Zerlegung entlang der -Spalte der Matrix hat die Form: und die Zerlegung entlang der -Zeile der Matrix:

Nachweisen:

Betrachten Sie die -Spalte der Matrix und schreiben Sie sie in der Form: gemäß der 6. Eigenschaft der Determinanten:

Determinantenmatrix Lagrangian mathematisch

Auf ähnliche Weise wird die Formel für die Zerlegung in der -Zeile einer Matrix bewiesen.

Satz 2

Es gelten folgende Gleichheiten:

Betrachten Sie eine Matrix, die wie folgt aus einer Matrix erhalten wird: Alle Spalten der Matrix, mit Ausnahme der dritten Spalte, sind mit denen der Matrix identisch. Die Spalte der Matrix stimmt mit der -ten Spalte überein, dann haben sie zwei identische Spalten, sodass die Determinante der Matrix gleich Null ist. Erweitern wir die Determinante der Matrix in der -ten Spalte.

Dann. Formel (2) wird ähnlich dargestellt.

Folge:

Determinante des Matrixprodukts

Feld der Skalare,

Sei die Elementarmatrix geordnet, dann gilt die Gleichheit:

1) ., d.h. wird aus der Matrix durch Multiplikation der -Zeile mit einem Skalar erhalten. Matrixdeterminante.

Die Matrix erhält man durch Multiplikation der -Zeile mit einem Skalar, also der Determinante

Durch Addition zu -row erhaltene Matrix

• -Elementarmatrizen
• 1) folgt der Beweis aus Lemma 1

2), Beweis aus Aussage (1) vorgelegt

Satz 1

Die Determinante des Produkts zweier Matrizen ist gleich dem Produkt ihrer Determinanten, d.h.

Nachweisen:

Seien die Zeilen der Matrix linear unabhängig, dann gibt es eine Kette elementarer Transformationen

dann folgt aus Lemma 2 das. Von what () haben wir: , dann

2) Die Zeilen sind linear abhängig, dann gibt es eine Kette elementarer Transformationen, die in eine Staffelmatrix übersetzt werden, die eine Nullzeile hat, d. h. , . Dann

Aus der Tatsache, dass es im Produkt auch eine Nulllinie gibt, weil

Notwendige und ausreichende Bedingungen dafür, dass die Determinante gleich Null ist

Feld der Skalare, - Matrix über dem Feld

Satz 1

Zeilen (Spalten) der Matrix sind linear abhängig

Angemessenheit:

Wenn die Zeilen (Spalten) einer Matrix linear abhängig sind, dann ist eine Zeile eine lineare Kombination anderer Zeilen (jeweils 8 Eigenschaften von Determinanten).

Notwendigkeit:

Lassen. Beweisen wir, dass die Zeilen linear abhängig sind. Angenommen, die Strings sind linear unabhängig, dann gibt es eine Kette elementarer Transformationen, die übersetzt werden. Aus dem, was in Punkt II bewiesen wurde, ergibt sich Folgendes. Wir haben einen Widerspruch erhalten. Lassen Sie uns beweisen, dass, wenn die -Zeile der Matrix linear abhängig ist, aber (die Anzahl der Spaltenvektoren) linear abhängig ist.

Satz 2

Folgende Bedingungen sind gleichwertig:

• 2) - linear abhängig
• 3) -reversibel
• 4) kann als Produkt elementarer Matrizen dargestellt werden

Nachweisen:

bewiesen in Satz 1

Matrixpartitionierung

Wenn Matrix, Matrix, Matrix und Matrix in der Form geschrieben werden

Dann bilden sie eine Matrix. In diesem Fall können sie als Matrixblöcke bezeichnet werden. Und entsprechend gekennzeichnet. Darstellung (1) wird Matrixpartitionierung genannt.

Wenn das Matrixprodukt existiert und in Blöcke unterteilt ist und die Aufteilung entlang der Spalten der Matrix der Aufteilung entlang der Zeilen der Matrix entspricht, können wir erwarten, dass es durch die Formel gegebene Blöcke hat

Daher gehen wir davon aus, dass das Produkt der Matrizen in Form von Blöcken, die durch entsprechende Partitionierung der Faktoren erhalten werden, formal mit dem Produkt dieser Matrizen in Form von Skalarelementen übereinstimmt. Lassen Sie uns dies anhand eines Beispiels zeigen:

Übung 1. Lassen

Dies kann durch direkte Berechnung überprüft werden

Satz (1)

Die Matrix soll Blöcke haben, bei denen es sich um eine Matrix handelt, und die Matrix von hat Blöcke der Größe. Dann hat es Blöcke

Nachweisen. Beachten Sie, dass jedes Produkt existiert und eine Matrix ist. Deshalb gibt es und wird es eine Matrix geben. Für „fixed“ hat jede Spalte und für „fixed“ jede Zeile, was bedeutet, dass es sich um Blöcke einer Matrix handelt.

Sei ein Matrixelement, das sich in einer Blockzelle befindet. Da es in Zellen und Matrizen eine Summe von Elementen gibt, . Aber das Matrixelement in einer Zelle ist die Summe der Produkte der Elemente in der Matrixzeile und der Elemente in der Matrixspalte. Darüber hinaus stimmen die Elemente der Zeile der Matrix mit einigen Elementen der Zeile in überein, nämlich mit, wobei der Index durch die Ungleichungen bestimmt wird

Die Elemente der Matrixspalte sind die Elemente in. Somit,

Für die Determinante haben wir Nebenordnungen definiert. Wenn wir aus einer Matrix alle Zeilen außer Zeilen und alle Spalten außer Spalten entfernen, dann wird die Determinante der resultierenden Matrix im Allgemeinen als Minor der Ordnungsmatrix bezeichnet

Minderjährige werden für die Matrix als Hauptdarsteller bezeichnet. Wenn es sich um eine Matrix handelt, dann ist es beispielsweise das algebraische Komplement

Wenn eine quadratische Matrix das Produkt einiger Matrizen (die rechteckig sein können) ist, ist es manchmal wichtig, die Determinante des Produkts anhand der Eigenschaften der Faktoren auszudrücken. Der folgende Satz ist ein aussagekräftiges Ergebnis dieser Art.

Kommentar. Die Operation der Matrixmultiplikation ist nicht kommutativ, d. h. Wenn das Produkt AB existiert, kann es sein, dass BA aufgrund der Nichtübereinstimmung der Abmessungen überhaupt nicht existiert (siehe das vorherige Beispiel). Wenn sowohl AB als auch BA existieren, können sie unterschiedliche Dimensionen haben (falls).

Für quadratische Matrizen gleicher Ordnung existieren die Produkte AB und BA und haben die gleiche Dimension, ihre entsprechenden Elemente sind jedoch im Allgemeinen nicht gleich.

In einigen Fällen fallen jedoch die Produkte AB und BA zusammen.

Betrachten Sie das Produkt einer quadratischen Matrix A und einer Identitätsmatrix E derselben Ordnung:

Das gleiche Ergebnis erhalten wir für das Produkt EA. Also gilt für jede quadratische Matrix A AE = EA = A.

Inverse Matrix.

Definition 3.7. Eine quadratische Matrix A heißt singuläres if und nichtsinguläres if.

Definition 3.8. Eine quadratische Matrix B heißt die Umkehrung einer quadratischen Matrix A gleicher Ordnung, wenn AB = BA = E. In diesem Fall wird B bezeichnet.

Betrachten wir die Bedingung für die Existenz einer zu einer gegebenen inversen Matrix und die Methode zu ihrer Berechnung.

Satz 3.2. Damit eine inverse Matrix existiert, ist es notwendig und ausreichend, dass die ursprüngliche Matrix nichtsingulär ist.

Nachweisen.

1) Notwendigkeit: seitdem (Satz 3.1), also

2) Suffizienz: Legen Sie die Matrix in der folgenden Form fest:

Dann ist jedes Element des Produkts (oder), das nicht auf der Hauptdiagonale liegt, gleich der Summe der Produkte der Elemente einer Zeile (oder Spalte) der Matrix A mit den algebraischen Komplementen zu den Elementen einer anderen Spalte und daher ist gleich 0 (als Determinante mit zwei gleichen Spalten). Die Elemente auf der Hauptdiagonale sind gleich. Somit gilt:

*=. Der Satz ist bewiesen.

Kommentar. Formulieren wir noch einmal die Methode zur Berechnung der inversen Matrix: Ihre Elemente sind die algebraischen Komplemente zu den Elementen der transponierten Matrix A, dividiert durch ihre Determinante.