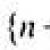Parallel and series connection of resistors, capacitors and inductors. Connection of components Series connected capacitor and coil

Assume as before that the current in the circuit varies according to the law

and calculate the voltage between the ends of the circuit u. Since when the conductors are connected in series, the voltages are added, the desired voltage u is the sum of three voltages: resistance, capacitance and inductance, and each of these voltages, as we have seen, changes over time according to the cosine law:

, (5)

, (6)

To add these three oscillations, we will use a vector voltage diagram. Voltage fluctuations across the resistance are represented on it by a vector directed along the current axis and having length , while voltage fluctuations across capacitance and inductance are represented by vectors and perpendicular to the current axis with lengths ( I m/w C) And ( I m w L) (Fig. 9.). Let's imagine that these vectors rotate counterclockwise around a common origin with angular velocity w. Then the projections onto the current axis of the vectors , and , will be described respectively by formulas (5)-(7). Obviously, the projection onto the current axis of the total vector

equal to the sum, that is, equal to the total voltage on the circuit section. The maximum value of this voltage is equal to the vector modulus. This value is easily determined geometrically. First, it is advisable to find the modulus of the vector:

,

and then according to the Pythagorean theorem:

. (8)

It is also clear from the figure that

. (9)

For the voltage on a section of the circuit, we can write

where the voltage amplitude and the phase shift between current and voltage are determined by formulas (8), (9). If , then the voltage leads the current in phase, otherwise the voltage lags behind the phase.

Formula (8) is similar to Ohm's law in the sense that the voltage amplitude is proportional to the current amplitude. Therefore, it is sometimes called Ohm's law for alternating current. However, it must be remembered that this formula applies only to amplitudes, but not to instantaneous values ​​and . Size

is called the circuit resistance for alternating current, the value

is called the reactance of the circuit, and the value R- active resistance.

The resulting formulas are also valid for a closed circuit that includes an alternating voltage generator, if under R, C And L understand their meanings for the entire chain (for example R represents the total active resistance of the circuit, including the internal resistance of the generator). In this case, all formulas should be replaced u on the emf of the generator. Indeed, for all our reasoning it was indifferent to where exactly the capacitance, inductance and resistance are concentrated, therefore in a closed circuit (Fig. 8) we can consider what the total active resistance of the circuit is, including the internal resistance of the generator, and - capacitance and inductance of the circuit, and replace the real generator with an imaginary one, whose internal resistance is zero. In this case, the voltage u between points a And b will be equal to the emf of the generator. It follows that formulas (8), (9) are also valid for a closed alternating current circuit, if by , , and we understand their meanings for the entire circuit and replace them in all formulas u on the emf of the generator.

According to the equations of the elements

. (15.1)

We found a current complex. Along the way, in the denominator we received the complex resistance of the two-terminal network , active resistance of a two-terminal network and reactance of a two-terminal network .

Phase resonance A two-terminal network is a mode in which the current and voltage of the two-terminal network are in phase: . In this case, the reactance and reactive conductivity of the two-terminal network are equal to zero.

Voltage resonance A two-terminal circuit is called a mode in which the voltages of the circuit elements are maximally compensated. The impedance of the two-terminal network is minimal.

Resonance of currents A two-terminal circuit is called a mode in which the currents of the circuit elements are maximally compensated. The total resistance of the two-terminal network is maximum.

For a series connection of a resistor, inductor and capacitor, the phase resonance coincides with the voltage resonance. The resonant frequency is determined by the formula

which is derived from the equality to zero reactance: .

Dependence of effective voltage values ​​on frequency for a series connection R, L, C shown in Fig. 15.3. Expressions for calculating these voltages are obtained by multiplying the effective current value (formula 15.2) by the impedances of the elements: , , (see paragraph 12).

Let's construct a vector diagram of current and voltage (Fig. 15.4, the case is shown here U L > U C). The easiest way to do this is if the initial phase of the current is zero: . Then the vector representing the current complex will be directed at an angle to the real axis of the complex plane. The voltage across the resistor is in phase with the current, so the vector representing the voltage complex across the resistor will be directed in the same direction as the vector representing the current complex.

Rice. 15.3.

Rice. 15.4.

Rice. 15.5.

The voltage on the inductor is ahead of the current in phase by an angle , so the vector representing the voltage complex on the inductor will be directed at an angle to the vector representing the current complex. The voltage on the capacitor lags in phase from the current by an angle , so the vector representing the voltage complex on the capacitor will be directed at an angle – to the vector representing the current complex. The vector representing the complex of the applied voltage will be equal to the sum of the vectors representing the complex voltages on the resistor, capacitor and coil. The lengths of all vectors are proportional to the effective values ​​of the corresponding quantities. That is, in order to draw vectors, you need to set the scale, for example: 1 centimeter is 20 volts, 1 centimeter is 5 amperes.

The vector diagram for the resonance mode is shown in Fig. 15.5.

Let's calculate the ratio of the effective voltage values ​​on the inductor and on the capacitor to the effective value of the source voltage in resonance mode.

Let us take into account that during resonance, the voltages on the coil and on the capacitor completely compensate each other (voltage resonance), and therefore the source voltage is equal to the voltage on the resistor: (Fig. 15.5). We use the relationship between the effective values ​​of current and voltage for the resistor, coil and capacitor, as well as the formula for the resonant frequency. We get:

where .

The quantity is called wave impedance oscillatory circuit and is designated by the letter r. The relation is denoted by the letter Q and is called quality factor oscillatory circuit. It determines the amplification properties of the circuit at the resonant frequency. In good circuits, the quality factor can be on the order of several hundred, that is, in resonance mode, the voltage on the coil and capacitor can be hundreds of times greater than that applied to the two-terminal network.

Resonance is often used in electrical engineering and electronics to amplify sinusoidal voltages and currents, as well as to separate oscillations of certain frequencies from complex oscillations. However, unwanted resonance in information electrical circuits leads to the emergence and intensification of interference, and in power circuits it can lead to dangerously high voltages and currents.

When a coil and a capacitor are connected in series in a design diagram, each of these elements of the electrical circuit can be represented by active and reactive resistances or active and reactive conductivities.

For calculations, a simpler diagram is Fig. 14.1, a, where the elements are connected in series, and in the diagram in Fig. 14.1, b they are connected mixed.

Let us assume that the parameters of the coil R1, L and the capacitor R2, C are known; circuit current i = I m sinωt.

It is necessary to determine the voltage in the sections of the circuit and the power.

Vector diagram and target impedance

The instantaneous value of the total voltage can be represented by the sum of the instantaneous voltages on the individual elements of the circuit:

u = u 1R + u L + u C + u 2R ,

I mean phase mismatch active and reactive voltages, the total voltage is obtained by vector addition:

U = U 2R + U L + U C + U 2R

To construct a vector diagram we find:

U 1R = IR 1; U 2R = IR 2 ; U L = IX L ; U C = IX C .

Depending on the ratio of the inductance and capacitance reactance values, three cases can be noted:

1. X L >X C . For this case, the vector diagram is shown in Fig. 14.2. The diagram shows voltage triangles for the coil and capacitor and finds the voltage vectors U 1 and U 2 on these elements.

Vector sum of voltages U 1 + U 2 = U gives the total voltage in the circuit. At the same time, vector U is the hypotenuse of a right triangle of voltages, the legs of which are the active and reactive voltages of the circuit ( U a And U r ). Since the vectors of the active voltage components are directed in one direction, their numerical values ​​add up: U a = U 1R + U 2R.

The vectors of the reactive voltage components are directed along one straight line in opposite directions, so they are given different signs: The reactive inductance voltage is considered positive, and the capacitance voltage is considered negative: U p = U L - U C.

With the same current in all elements of the circuit U L >U C . Current lags behind the overall voltage in phase per angle φ . From the stress triangle it follows

Where R = R 1 + R 2 And X = X L - X C total and active and reactance resistance of the circuit. The total resistance of the circuit is Z.

These resistances can be graphically represented by the sides of a right triangle of resistances, which is obtained in a well-known way from a triangle of voltages.

Circuit impedance Z is the coefficient of proportionality between the effective values ​​of the current and the total voltage of the circuit:

U = IZ; I = U/Z; Z = U/I.

From the voltage and resistance triangles, the following quantities are determined:

The phase shift angle between voltage and current in the circuit is positive ( φ >0) (phase currents are counted from the current vector).

2. X L< Х C The vector diagram is shown in Fig. 14.3, where U L φ <0.

Re the active resistance of the circuit is capacitive in nature .

The calculation formulas for the first case remain unchanged for the second case.

3. X L = X C . In this case, the reactive voltage components of the coil and capacitor are equal in magnitude and mutually compensated: U L = U C (Fig. 14.4). Therefore, the reactive component of the total voltage and the total reactance are equal to zero, and the total resistance of the circuit Z = R.

The total voltage is in phase with the current and is equal in magnitude to the active

voltage component.

The phase angle φ between the current and the total voltage is zero.

The current in the circuit and the total voltage are related by the formula

U = IR, or I = U/R.

In the case of X L = X C, the phenomenon of voltage resonance occurs in the circuit.

Energy process in a circuit with a series connection of a capacitor and a coil

From the voltage triangle it is easy to obtain a power triangle from which the already known formulas follow:

Reactive powers are also included in calculations with different signs: inductive power is positive and capacitive power is negative.

In accordance with this, the sign of the reactive power of the entire circuit can be one or the other, as follows from formulas (14.2).
At φ>0 Q>0 ; at φ<0 Q<0.

Active power is positive at any angle, since cos φ =cos(- φ ).

Apparent power is also always positive. Based on formulas (14.2), we can conclude that in the circuit under consideration there is a transformation of electrical energy (P ≠ 0) and an exchange process between the generator and the receiver (Q ≠ 0 at φ ≠ 0).

Energy processes in this case are more complex than in the previously discussed simple circuits. The complication is explained by the fact that, along with the exchange of energy between the generator and the receiver, there is an exchange of energy inside the receiver, between the coil and the capacitor.

Features of the energy process in a circuit with a series connection of a coil and capacitors are shown in Fig. 14.5, which shows graphs of the instantaneous power of individual elements and the circuit as a whole at X L = X C.

The coil and capacitor accumulate equal amounts of energy during a half cycle. However, in the first quarter of the period, when the current increases and the voltage across the capacitor decreases, energy accumulates in the magnetic field of the coil and decreases in the electric field of the capacitor, and the rate of change of energy (power) is the same at any time. This gives grounds to believe that energy exchange occurs only in the receiver between the coils
and a capacitor.

To convert electrical energy into another form, the receiver receives it from a generator with an average speed (power) R.

Problems on the topic and an example of solving a problem for a circuit with a series connection of a capacitor and a coil