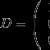Calculation scheme. “VBA Algorithm Development. Block diagram. Algorithm structures. Input and output operators in the Pascal programming language

The daily life of every person involves solving a huge number of tasks of varying complexity at work or while studying. Some tasks are so simple that when we perform them, we do certain actions automatically, without even thinking. The solution to any problem, even the simplest one, is usually carried out sequentially in several steps. This kind of sequence when solving problems is called an algorithm. Today we will look at what linear algorithms are, how their structure is depicted, how they are solved and programmed.

Algorithmic language

This concept is a precise instruction for the performer to perform a certain sequence of actions, which is aimed at solving the task.

This language is a means of describing algorithms that are usually user-oriented.

• Algorithm start-end block. On the block there is an inscription “beginning” or “end”.
• Data input/output block. This block is depicted as a parallelogram. The following inscriptions are placed on it: “input”, “output”, “print”. They are also accompanied by a list of input or output variables.
• Arithmetic block, or decision block. It corresponds to a rectangle. The block should have the inscription: “operation”, “group of operations”.

With the help of such block diagrams the solution of linear algorithms is depicted. Next, let's talk about the features of assigning values.

Linear computational algorithms

The main elementary action in a computational algorithm is assigning a certain value to a variable. In the case when the value of a constant is determined by the type of its notation, the variable value will receive a specific value solely as a result of assignment. This can be done in two ways: using the assignment command; using the input command.

An example of a linear algorithm solution

Let us give an example of a description of the rules for dividing ordinary fractions using a linear algorithm, which in school textbooks have the following content:

• the numerator of fraction 1 must be multiplied by the denominator of fraction 2;
• the denominator of fraction 1 must be multiplied by the numerator of fraction 2;
• you need to write down a fraction in which the numerator is the result of completing 1 point, and the denominator is the result of completing 2 points. The algebraic form of this rule is as follows:

a/b: c/d=(a*d)/(b*d)=m/n.

So, let's build an algorithm for dividing fractions for a computer. In order not to get confused, we will use the same notation for variables as in the formula indicated above. a, b, c, d - source data in the form of integer variables. The result will also be integer values. The solution in algorithmic language will be as follows:

alg Division of fractions

intact a, b, c, d, m, n

input a, b, c, d

con

Graphic form of the solution

The diagram of the linear algorithm described above looks like this:

The value assignment command has the following format:

Variable:=expression.

The “:=” sign is read as assign.

Assignment is a command that is necessary for the computer to perform the following actions:

• expression calculations;
• assigning the resulting value to a variable.

The above algorithm contains two commands as assignment. In a block diagram, the assignment instruction must be written in a rectangle called a computation block.

When describing linear algorithms, there is no particular need to strictly follow strict rules when writing expressions. You can write them using the usual mathematical form. After all, this is not the strict syntax of a programming language.

In the example algorithm given there is also an input command:

Enter a, b, c, d.

The input command in a block diagram is written in a parallelogram, that is, in an input-output block. By executing this command, the processor interrupts operation until the user performs certain actions. Namely: the user needs to type the input variables (their values) on the (keyboard) and press Enter, which acts as the enter key. It is important that the values ​​are entered in the same order as the corresponding variables located in the input list.

Linear algorithm. Its programming

As mentioned at the beginning of the article, linear programs can include the following statements:

• assignment;
• input;
• conclusion.

That is, using the listed operators, algorithms are implemented.

So, in program language it is written like this:

LET A = B, where A is a variable, B is an expression. For example, A = Y + 20.

The input statement looks like this:

INPUT, for example: INPUT C

The operator for outputting data, values, is written in the following form:

PRINT. For example PRINT S.

Let's give a simple example. We need to write a program that will find the sum of numbers A and B entered from the keyboard.

In a programming language, we will get a program, the text of which is shown below.

Input and output operators in the Pascal programming language

Pascal does not provide special operators to indicate the input or output operations that linear algorithms use. In programs, information is exchanged using built-in procedures. Since there is no need for a preliminary description of the standard procedure, it is available to every program that contains a call to it. Also, the name of the procedure mentioned is not any reserved word.

When entering data, such operators are used to refer to a standard data entry procedure that is already built into the program.

Read (A, B, C), where A, B, C are variables that need to be entered into RAM for memorization.

Readlnn (x1, y, x2) - after finishing the input, the cursor moves to the beginning of a new line.

Readlnn; - indicates that you are waiting to press “Enter”. Typically, this statement is inserted into the text before the last “End” to save the results of program execution on the content screen.

Data is displayed on the monitor screen using the following operators:

Write (A, B, C) - by specifying the values ​​A, B, C in one line, the cursor does not leave the current line.

Writeln (z, y, z2) - having finished outputting values, the cursor at this position will move to a new line.

Writeln; - indicates skipping one line and moving to the beginning of a new one.

It is with the help of such simple operators that data is input and output in the Pascal language.

summary of other presentations

“Basic algorithmic structures” - Execution of “loop body” commands. Block diagram of the algorithmic structure "branching". Let n=5; i=4. Block diagram of the cyclic algorithm. End. Algorithmic structure "choice". Let n=5; i=5. Start. Branching structure. Let n=5; i=6. Basic types of algorithmic structures. Algorithmic structure "cycle". Positive number. Flowchart of the “choice” algorithmic structure. Linear algorithm block diagram.

“Types of algorithms” - Apartment cleaning. Open the bag. Lesson motto. Towers of Hanoi. Name of the figure. Watch the cartoon. Harvest the harvest. Introduction to the algorithm. Approach the crossing. Cyclic algorithms. Enter the garden. Palms. Algorithm of human actions. Graphic dictation. Recording algorithms. Algorithm.

Recording a cycle in a procedure. Correction of the procedure. Primary colors. Let's draw a wall. What is an Algorithm? Team. Interactive tutorial. Drawing the roof. Let's draw a house. Let's draw. We draw windows. The house is ready. Cycle. Knowledge. Change pen color.

“Linear algorithm problems” - X = 0 There are no solutions. Y = 2. X = 3 Y = 1/48. The coordinates of the vertices of triangle ABC are given. Calculate the value of the Y function at X=2 using the algorithm flowchart. Convert A to larger units of information. Algorithmization is the process of developing an algorithm (action plan) to solve a problem. X = -1 There are no solutions. Examples of problem solving. The lengths of the sides of the triangle A, B, C are given. Find the area of ​​the triangle S. Make a block diagram of the algorithm for solving the problem.

“Algorithmic constructions” - A method of representing algorithms in the form of a graph. Branching. Presentation of algorithms in the form of a description of a sequence of actions. Forms of presentation of algorithms. Flowchart of the “Wallpapering” algorithm. Algorithmic designs. Algorithm for solving the problem. Block diagram. Graphical way of presenting algorithms. Methods of presenting algorithms. Algorithm. Complex algorithm. Block diagrams of basic structures.

“Main types of algorithmic structures” - Write algorithms in verbal form. Work in groups. Structure. Spelling of prefixes. Basic types of algorithmic structures. Checking independent work. Physical exercise. Tasks to consolidate knowledge. Algorithm. Basic structure. Setting initial parameters. Recipe for making tea. Branching. Find the root. Loop with postcondition. Cycle. Block characters. End of the algorithm. Main types of agrorhythmic structures.

General instructions
To synthesize the circuits in Sect. 5.1 describes the following steps:
1. Description of the function of the required circuit.
2. Assignment of input and output variables and assignment of values ​​0 and 1.
3. Drawing up a truth table.
4. Determination of the necessary logical operations.
5. Simplification and, if necessary, transformation of the circuit.
If the truth table is known, then it is now advisable to start the 4th stage with the compilation of the normal form of OR. It will be simplified as much as possible using a Carnot diagram. At the end of step 4, a simplified logic function is obtained, which can be used to assemble a logical digital circuit.
Step 5 checks whether further simplification of the function found using logical algebra is possible and rational. If yes, then simplification must be carried out.
Now we need to find out what logical elements are available. The logical function must be transformed so that it contains only the available logical elements. Then you can assemble the circuit.

Digital on/off circuit from multiple locations

Using logic gates, you need to synthesize a circuit that functions as an on/off circuit from multiple locations. The output state should change only if the state of one of the inputs changes. If both inputs change their state, then the output state should not change. The circuit must be built on OR-NOT elements.
The desired circuit has two inputs and one output. The input variables are called A and B. The output variable is called Z (Figure 5.47).
The truth table of a circuit with two input variables has 4 options (Fig. 5.48). The initial state Z for the first option can be set in any way. Selected Z = 0.
When moving from option 1 to option 2, variable A changes its state. Variable B does not change the state. If only one of the inputs changes state, then according to the given task, output Z must change its state. Z must be equal to 1.
When moving from option 2 to option 3, variables A and B change their states. Z should not change. When moving from option 3 to option 4, variable A changes its state from 0 to 1. B remains equal to 1. Thus, Z must change state from 1 to 0. The truth table is ready. It might look different if we had chosen Z= 1 in option 1.
For the truth table (Fig. 5.48), you need to write down the normal form OR. It looks like this:
Z = (AaB)w(AaB).
If you enter the normal form OR into the Carnot diagram, you can see that further simplification is impossible (Fig. 5.49).
Since the circuit must be built on OR-HE elements, it is necessary to transform the equations:
Z = (AaB)w(AaB)-,
Z = (AaB)v(AaB),
Z = AaBaAaB.

Rice. 5.50 Digital circuit

The circuit constructed according to the transformed equation is shown in Fig. 5.50.

Two out of three switch

Systems associated with increased risk, such as a nuclear power plant, must be immediately shut down in the event of an accident. Shutdown occurs automatically using a digital circuit. False alarms may occur in emergency sensors responsible for shutdowns. Therefore, three identical emergency sensors are installed in each critical location (Fig. 5.51).
Shutdown should only occur when at least two of the three alarm sensors are triggered. This approach prevents unnecessary system shutdowns that cause financial losses. When triggered, emergency sensors have state 1. The system should be turned off if state 1 is active at the output of the circuit.
So, what is required is a circuit whose output is at state 1 when at least 2 of the 3 inputs are at state 1. This circuit is called a two-out-of-three switch.
The input variables are named A, B and C. The output variable is Z. Let's create a truth table using a verbal description of the principle of operation of the circuit. Whenever two input variables are equal to 1, Z = 1. If all three input variables are equal to 1, Z must also be equal to 1. Such a truth table is shown in Fig. 5.52.
Next, according to the compiled truth table, the normal form OR is written:

Rice. 5.51.

Z = (A a B a C) v (A a B a C) v a5aC|v(^aSaC).

The normal form of OR is simplified using a Carnot diagram (Fig. 5.53). Three double groups can be formed. The simplified equation is:
Z = (AaB)w(BaC)w(AaC).
Using this equation, you can build a diagram (Fig. 5.54).
Often only OR-HE elements are at hand. To build a circuit using only OR-HE elements, we transform the equation: into °-
Z = (AaB)v(BaC)v(AaC);
======= S O.
Z = (A l B)v (B aC)v (A lC);
—=====—= Fig. 5.55. Switch circuit "two"
Z = AlVlVlSlAlS. of three" on Sh1I-NE elements.
The corresponding diagram is shown in Fig. 5.55.

Parity circuit

To detect errors in codes (see Sections 8.7 and 8.8), as well as for control and monitoring tasks, a circuit is often required in which the output is 1 when an even number of inputs are 1.
This circuit is called a parity circuit.
It is required to synthesize a circuit with four inputs. The input variables are A, B, C and D. The output variable is Y.
First you need to create a truth table. Y will always be equal to 1 if 0, 2 or 4 input variables are equal to 1 (Figure 5.56).
From the truth table we obtain the normal OR form:
Y = (A l V lS l D)\/ ^A l V lS l (A l V lS l (A l V aS l
v(A l V lS l [A l V lS l (A l V lS l (A l V lS l D).

Individual complete conjunctions are numbered. Let's try to simplify the normal form of OR using a Karnaugh map (Fig. 5.57). Here we are faced with a rare case where the formation of groups is impossible. This means that this normal form of OR cannot be simplified, and its diagram is shown in Fig. 5.58.

A threshold logic circuit is a circuit in which a certain minimum number of input variables must have a state of 1 in order for a logical 1 to appear at the output.
For example, you need to calculate a circuit with five input variables. The output should be 1 only when at least 4 inputs are 1.
The input variables are named A, B, C, D, and E. The output variable is Z. First, we need to define the truth table. With five variables, 32 options are possible (Fig. 5.59):
Z =¦ (A l V lS l D l E^v (A l V lS l D l E)v (A l V lS l D l v^A l V lS l D l E^v [A l V lS l D l E^v (A l B lS l D l E).
Normal form OR consists of six complete conjunctions.
The normal form of OR is simplified using a Carnot diagram (Fig. 5.60). You can form 5 double groups. This results in the following simplified logical function:
Z = (A aBaCaE)v (A aBaDaE)v (A aBaCaD)v v(A aC a D a E)v (B aC a D a E).

The diagram for the simplified function is shown in Fig. 5.61. This equation can be further simplified using the algebra of logic. For the first three complete conjunctions we can put out of brackets (AaB), for the last two - (C l D). The resulting function is:
Z = [(A A B) A ((C A E) V (D A E) A C A X>))] V [(C A D) A ((A A E) V (B A Z))] . Still, it was not possible to achieve significant simplification.

Comparison circuit (comparator)

In digital technology, you often need to compare digital data with each other. The simplest comparison circuit, the so-called comparator, compares the state of two variables with each other.
Let the variables be labeled A and B. A and B can be equal. A may be greater than B and vice versa. The comparator has three outputs for these three possible options. They are designated X, Y and Z and their states are assigned as follows:
A = Z => X = 1;
A > B^> Y= 1;
A< В =>Z = 1.
So, it is necessary to synthesize a circuit with two input variables A and B and output variables X, Y and Z.
When forming a truth table, you should follow the rules: A is greater than B if A = 1 and B = 0. Accordingly, B is greater than A if B = 1 and A = 0. The truth table is shown in Fig. 5.62.
Logical functions are obtained from the truth table:
X = (AaB)v(AaB);
Y = A a B;
Z = A a B.
These equations are not simplified further. The desired scheme is shown in Fig. 5.63.

Rice. 5.62.

Rice. 5.63.

Before leaving the factory, transistors are checked to ensure that four important parameters A, B, C and D are within the acceptable range. Four digital sensors are used for measurement. The sensor outputs 1 if the measured value is within the range of acceptable values. If the measured value is outside the range of acceptable values, the sensor outputs 0.
Transistors are sorted using a digital circuit. If all four values ​​are within the range of acceptable values, the output variable M becomes 1. If only B is outside the range of acceptable values, then the output variable N becomes 1. If only B and D are outside the range of acceptable values, then the output variable U receives state 1. In all other cases, the output Z is 1, which means that the transistor is defective.
It is required to calculate the circuit and build it only on NAND elements (also called “in the NAND basis”).
The inputs are four variables A, B, C and D. The output variables are M, N, U and Z. M becomes 1 if A = 1, 5 = 1, C = 1 and D = 1. This is option 16 in truth table (Fig.
5.64). will be 1 if A = \, 5 = 0, C = 1 and D = 1 (option 14). U will be equal to 1 if A is 1, 5 = 0,
C = 1 and D = 0 (option 6). In all other cases, except 6, 14 and 16, Z— 1.

Rice. 5.64. Truth table for transistor sorting circuit. For greater clarity, zeros for the output variable are not written

The result is the following logical functions:
M = AaBaCaD;
N = A a B a C a D; U = A a B aC a D. Function Z contains 13 complete conjunctions. Z is then always 1 if neither M, N, nor U equals 1. It is better to write the normal OR form for Z (see Fig. 5.64):
Z = (^4a5aCaD)v^a5aCaD^v^aBaCaZ));
Z = M v N vU. Then for the direct value of Z:
Z = M v N vU.

Rice. 5.65.

The functions found for M, Nn U cannot be simplified. They must be recalculated together with the equation for Z to the NAND basis:
M = AaBaCaD\
N = A a B aC l D;
U = AlVlSlO",
Z = M v N v U = M a N aU;
Z = M a N a U.
From these equations the diagram shown in Fig. is obtained. 5.65. Through the outputs M, N, U and Z, a mechanical device can be controlled that distributes the transistors into 4 different containers.

When implementing analog signal processing algorithms, it is often necessary to calculate mathematical functions. The most common functions are logarithmic and exponential functions. These functions are used in schemes to reduce and increase the dynamic range of a transmitted or recorded signal (companding). Another common application of exponent and logarithm math circuits is to calculate the product and division of input signals.

To calculate a nonlinear function, an operational amplifier surrounded by negative feedback is often used. As an example, Figure 1 shows the circuit of a logarithmic amplifier.

Figure 1. Logarithmic amplifier circuit

In this circuit, a nonlinear element (semiconductor diode) is included in the negative feedback circuit, which has an exponential dependence of the current on the applied voltage. As a result of the feedback action, the dependence of the output voltage on the input becomes logarithmic. The gain of this logarithm circuit is determined by R1. Typically, the logarithm circuit is designed for unity gain.

If a diode with a quadratic current-voltage characteristic is used in this circuit, then it will calculate the square root of the input signal. It is convenient to use in circuits for determining signal amplitude during quadrature signal processing.

(1),

The inverse of the logarithmic function, the exponential, is calculated in a similar way. Only in this case the nonlinear element is not included in the feedback circuit, but at the input of the amplifier. Figure 2 shows a diagram for calculating the exponent on an operational amplifier.

Figure 2. Scheme for calculating the exponent

If a diode with a quadratic current-voltage characteristic is used in this circuit, then the circuit will calculate the square of the input voltage and can be used as a circuit for determining the input signal power.

Using these circuits for calculating mathematical functions, you can calculate the product of two analog signals. This uses the well-known property of logarithms to replace the product of variables with the sum of the logarithms of these variables. For the inverse conversion, the exponent calculation function is used. In this case, the base of the logarithm is completely unimportant.

(2),

The multiplier circuit that implements formula (1) on operational amplifiers is shown in Figure 3.

Figure 3. Operational amplifier multiplier circuit

Despite the simplicity of implementation, such a scheme is used quite rarely, because Multiplication is only possible for positive input values. Therefore, multiplier circuits built on the basis are usually used.

To calculate functions, it is not always possible to select a nonlinear element with a given current-voltage characteristic. In this case, you can use piecewise linear approximation of the function. It is easy to implement any gain on an operational amplifier simply by changing the value of the resistor in the feedback circuit, thereby setting the slope of the function. Switching resistors when the input voltage changes is easiest to do using diode switches, which are supplied with the turn-off voltage we set. A similar diagram is shown in Figure 4.

Figure 4. Function amplifier circuit

Transistor-based multipliers are often used to compute more complex functions. In the simplest case, the X and Y inputs can be combined to obtain a circuit for calculating the square of the input signal ( Y=X 2).

They can be used as electronic voltage regulators. By applying a constant voltage to one of the inputs, you can regulate the level of alternating voltage supplied to the output at the output.

Literature:

Together with the article "Schemes for calculating mathematical functions" read:

2.1 Development of the algorithm.

Algorithm- This

a. description of the sequence of actions to solve a problem or achieve a goal;

b. rules for performing basic data processing operations;

c. description of calculations using mathematical formulas.

Before starting to develop an algorithm, it is necessary to clearly understand the task: what is required to be obtained as a result, what initial data is needed and what is available, what restrictions exist on this data. Next, you need to write down what actions need to be taken to obtain the required result from the initial data.

In practice, the most common forms of presenting algorithms are:

Verbal (recordings in natural language);

Graphic (images from graphic symbols);

Pseudocodes (semi-formalized descriptions of algorithms in a conditional algorithmic language, including both elements of a programming language and natural language phrases, generally accepted mathematical notations, etc.);

Programming (texts in programming languages).

The verbal way of writing algorithms is a description of the successive stages of data processing. The algorithm is specified in a free form in natural language.

Example. Write down an algorithm for finding the greatest common divisor (GCD) of two natural numbers.

The algorithm could be as follows:

1. set two numbers;

2. if the numbers are equal, then take any of them as the answer and stop, otherwise continue executing the algorithm;

3. determine the largest of the numbers;

4. replace the larger number with the difference between the larger and smaller numbers;

5. repeat the algorithm from step 2.

The described algorithm is applicable to any natural numbers and should lead to a solution to the problem. Convince yourself of this by using this algorithm to determine the greatest common divisor of the numbers 125 and 75.

The verbal method is not widespread for the following reasons:

Such descriptions are not strictly formalizable;

Suffer from wordiness of notes;

There is room for ambiguity in the interpretation of individual regulations.

The graphical way of presenting algorithms is more compact and visual compared to the verbal one.

When presented graphically, the algorithm is depicted as a sequence of interconnected functional blocks, each of which corresponds to the execution of one or more actions.

This graphical representation is called a flowchart or flowchart.

Pseudocode is a system of notations and rules designed to uniformly write algorithms.

It occupies an intermediate place between natural and formal languages.

On the one hand, it is close to ordinary natural language, so algorithms can be written and read in it like regular text. On the other hand, pseudocode uses some formal constructs and mathematical symbolism, which brings the algorithm notation closer to the generally accepted mathematical notation.

In pseudocode, strict syntactic rules for writing commands inherent in formal languages ​​are not adopted, which makes it easier to write the algorithm at the design stage and makes it possible to use a wider set of commands designed for an abstract executor. However, pseudocode usually contains some constructs that are inherent in formal languages, which makes it easier to move from writing in pseudocode to writing an algorithm in a formal language. In particular, in pseudocode, as well as in formal languages, there are function words, the meaning of which is determined once and for all. There is no single or formal definition of pseudocode, so various pseudocodes are possible, differing in the set of function words and basic (basic) constructions.

2.2 Block diagram.

A flowchart is a graphical representation of an algorithm in which it is depicted as a sequence of interconnected functional blocks, each of which corresponds to the execution of one or more actions.

In the flowchart, each type of action (entering initial data, calculating the values ​​of expressions, checking conditions, controlling the repetition of actions, completing processing, etc.) corresponds to a geometric figure represented as a block symbol. Block symbols are connected by transition lines that determine the order in which actions are performed.

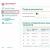
Here are the most commonly used symbols.

Symbol name	Designation and example of filling	Explanation
Process		Computational action or sequence of actions
Solution		Checking conditions
Modification		Start of the cycle
Predefined process		Calculations by subroutine, standard subroutine
Input Output		I/O in General
Start-stop		Beginning, end of the algorithm, entry and exit to the subroutine
Document		Printing results

The "process" block is used to denote an action or sequence of actions that changes the meaning, form of presentation or placement of data. To improve the clarity of the diagram, several individual processing blocks can be combined into one block. The presentation of individual operations is quite free.

The "decision" block is used to indicate conditional control transitions. Each "solution" block must identify the question, condition, or comparison that it defines.

The "modification" block is used to organize cyclic structures. (The word modification means modification, transformation). A cycle parameter is written inside the block, for which its initial value, boundary condition and step of changing the parameter value are indicated for each repetition.

The "predefined process" block is used to indicate calls to auxiliary algorithms that exist autonomously in the form of some independent modules, and for calls to library routines.

Example. Draw up a block diagram of an algorithm for determining the heights ha, hb, hc of a triangle with sides a, b, c, if

Where p = (a + b + c) / 2.
Solution. Let us introduce the notation then h a = t/a, h b = t/b, h c = t/c. The flowchart must contain start, input a, b, c, calculation p, t, h a, h b, h c , output the results and stop.

2.3 Algorithm structures.

Algorithms can be thought of as certain structures consisting of individual basic (i.e. basic) elements. Naturally, with this approach to algorithms, the study of the basic principles of their design should begin with the study of these basic elements

The logical structure of any algorithm can be represented by a combination of three basic structures: following, branching, and looping.

A characteristic feature of basic structures is the presence of one input and one output.

1. Basic structure follows. Formed from a sequence of actions following one after another:

2. Basic branching structure. Provides, depending on the result of checking the condition (yes or no), the choice of one of the alternative ways of operating the algorithm. Each path leads to a common output, so the algorithm will continue to run no matter which path is chosen.

Structure branching exists in four main variants:

If-then-else;

The choice is different.

1) if-if condition then action end if 2) if-else if condition then actions 1 otherwise actions 2 end if 3) choice choice with condition 1: actions 1 with condition 2: actions 2. . . . . . . . . . . . under condition N: actions N end of choice 4) choice - otherwise choice under condition 1: action 1 under condition 2: action 2. . . . . . . . . . . . under condition N: actions N otherwise actions N+1 end of choice

Example. Create a block diagram of the algorithm for calculating the function

The basic structure is a cycle. Provides repeated execution of a certain set of actions, which is called the body of the loop.

The cycle structure exists in three main versions:

Loop type For.

Instructs to execute the loop body for all values ​​of a certain variable (loop parameter) in a given range.

Loop type Bye.

Orders the body of the loop to be executed as long as the condition written after the word while is met.

Loop type do while.

Orders the body of the loop to be executed as long as the condition written after the word while is met. The condition is checked after the loop body is executed.

Note that loops for and while are also called loops with pre-checking the condition, and loops to do - while - loops with post-checking the condition. In other words, the bodies of the for and while loops may not be executed even once if the loop ending condition is not initially true. Do the body of the loop until it is executed at least once, even if the condition for ending the loop is not initially true.

Cycle for i from i1 to i2 step i3 cycle body (sequence of actions) end of cycle loop while condition loop body (sequence of actions) end of loop cycle do loop body (sequence of actions) until condition end of loop

with a given accuracy (for a given alternating power series, the required accuracy will be achieved when the next term becomes smaller in absolute value).

Calculating sums is a typical cyclic task. The peculiarity of our specific problem is that the number of terms (and, consequently, the number of repetitions of the loop body) is unknown in advance. Therefore, the loop must end when the required accuracy is achieved.

When compiling an algorithm, you need to take into account that the signs of the terms alternate and the power of the number x in the numerators of the terms increases.

Solving this problem head-on by calculating the partial sum at each i-th step

S:=S+(-1)**(i-1)*x**i/i ,

we will end up with a very inefficient algorithm that requires a large number of operations. It is much better to organize the calculations as follows: if you designate the numerator of any term by the letter p, then the numerator of the next term will be equal to -р*х (the minus sign ensures the alternation of the signs of the terms), and the term itself will be m

will be equal to p/i, where i is the number of the term.

An algorithm that includes an iterative loop is called an iterative algorithm. Iterative algorithms are used in the implementation of iterative numerical methods. In iterative algorithms, it is necessary to ensure that the condition for exiting the cycle is achieved (convergence of the iterative process). Otherwise, the algorithm will loop, i.e. the main property of the algorithm - effectiveness - will not be fulfilled.

Nested loops.

There may be cases when it is necessary to repeat a certain sequence of statements inside the body of a loop, that is, to organize an inner loop. This structure is called a loop within a loop or nested loops. The nesting depth of loops (that is, the number of loops nested within each other) can be different.

When using such a structure, to save computer time, it is necessary to move all statements that do not depend on the parameter of the inner loop from the inner loop to the outer one.

Example nested loops for. Calculate the sum of the elements of the given matrix A(5,3).

Example nested loops for now. Calculate the product of those elements of the given matrix A(10,10) that are located at the intersection of even rows and even columns.