Stokastik gradyan inişi. Uygulama seçenekleri. Stokastik Gradyan İnişi Çok Düzgün Pürüzsüzleşiyor

DVM

Destek vektör makinesi(İngilizce SVM, destek vektör makinesi) - sınıflandırma problemleri için kullanılan bir dizi benzer denetimli öğrenme algoritması ve regresyon analizi... Doğrusal sınıflandırıcılar ailesine aittir, ayrıca Tikhonov düzenlileştirmesinin özel bir durumu olarak da düşünülebilir. Destek vektör makinesinin bir özelliği, ampirik sınıflandırma hatasının sürekli olarak azalması ve boşluğun artmasıdır, bu nedenle yöntem, maksimum boşluk sınıflandırıcı yöntemi olarak da bilinir.

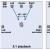
Yöntemin ana fikri, başlangıç ​​vektörlerini daha yüksek boyutlu bir uzaya aktarmak ve bu uzayda maksimum boşluk ile ayırıcı bir hiperdüzlem aramaktır. Sınıflarımızı ayıran hiperdüzlemin her iki tarafında iki paralel hiperdüzlem inşa edilmiştir. Bölen hiperdüzlem, iki paralel hiperdüzlemin mesafesini maksimize eden hiperdüzlem olacaktır. Algoritma, bu paralel hiperdüzlemler arasındaki fark veya mesafe ne kadar büyük olursa, ortalama sınıflandırıcı hatasının o kadar küçük olacağı varsayımıyla çalışır.

Genellikle makine öğrenimi algoritmalarında verileri sınıflandırmaya ihtiyaç vardır. Her veri nesnesi, boyutlu uzayda (p sayı dizisi) bir vektör (nokta) olarak temsil edilir. Bu noktaların her biri iki sınıftan yalnızca birine aittir. Noktaları bir hiper düzlem ile ayırıp ayıramayacağımızla ilgileniyoruz.Bu tipik bir lineer ayrılabilirlik durumudur. Bu tür birçok hiper düzlem olabilir. Bu nedenle, sınıflar arasındaki boşluğu en üst düzeye çıkarmanın daha güvenli bir sınıflandırmaya katkıda bulunduğuna inanmak doğaldır. Yani, en yakın noktaya olan uzaklığı maksimum olacak şekilde böyle bir hiperdüzlem bulabilir miyiz? Bu, hiperdüzlemin zıt taraflarında uzanan en yakın iki nokta arasındaki mesafenin maksimum olduğu anlamına gelir. Eğer böyle bir hiperdüzlem varsa, o zaman en çok bizi ilgilendirecektir; buna optimal bölen hiperdüzlem denir ve karşılık gelen lineer sınıflandırıcıya optimal bölen sınıflandırıcı denir.

Resmi olarak, sorun aşağıdaki gibi tanımlanabilir.

Noktaların şu şekilde olduğunu varsayıyoruz:, noktanın hangi sınıfa ait olduğuna bağlı olarak 1 veya 1 değerini alır. Her biri, genellikle veya değerleri ile normalize edilen, boyutlu bir gerçek vektördür. Noktalar normalize edilmezse, noktaların koordinatlarının ortalama değerlerinden büyük sapmalar olan nokta, sınıflandırıcıyı çok fazla etkileyecektir. Bunu, her öğenin ait olduğu önceden tanımlanmış bir sınıfa sahip olduğu bir öğrenme koleksiyonu olarak düşünebiliriz. Destek vektör makinesinin onları aynı şekilde sınıflandırmasını istiyoruz. Bunu yapmak için, aşağıdaki forma sahip bir ayırıcı hiperdüzlem oluşturuyoruz:

Vektör, bölen hiper düzleme diktir. Parametre mutlak değerde hiper düzlemden orijine olan mesafeye eşittir. Parametre sıfırsa, hiperdüzlem, çözümü sınırlayan orijinden geçer.

Optimal ayırma ile ilgilendiğimiz için, optimal olana paralel ve iki sınıfın destek vektörlerine en yakın destek vektörleri ve hiperdüzlemlerle ilgileniyoruz. Bu paralel hiperdüzlemlerin aşağıdaki denklemlerle (normalizasyona kadar) tanımlanabileceği gösterilebilir.

Eğitim örneği doğrusal olarak ayrılabilirse, aralarında eğitim örnek noktası kalmayacak şekilde hiperdüzlemleri seçebilir ve ardından hiperdüzlemler arasındaki mesafeyi maksimize edebiliriz. Aralarındaki şeridin genişliği geometri nedeniyle bulmak kolaydır, eşittir, bu yüzden görevimiz en aza indirmektir. Tüm noktaları şeritten çıkarmak için, tüm bunlardan emin olmalıyız.

Şu şekilde de yazılabilir:

Sınıfların lineer ayrılabilirliği durumunda, optimal bir ayırıcı hiperdüzlem oluşturma problemi, koşul (1) altında minimizasyona indirgenir. Bu, şuna benzeyen ikinci dereceden bir optimizasyon problemidir:

Kuhn - Tucker teoremi ile bu problem şuna eşdeğerdir: ikili görev Ara Eyer noktası Lagrange fonksiyonları.

İkili değişkenlerin vektörü nerede

Bu problemi, sadece ikili değişkenler içeren eşdeğer bir ikinci dereceden programlama problemine indirgeyelim:

Diyelim ki karar verdik bu görev, o zaman formüllerle bulunabilir:

Sonuç olarak, sınıflandırma algoritması şu şekilde yazılabilir:

Bu durumda, toplama tüm örneklem üzerinde değil, sadece destek vektörleri üzerindedir.

Sınıfların lineer ayrılamazlığı durumunda algoritmanın çalışabilmesi için eğitim setinde hata yapalım. Nesnelerdeki hatanın büyüklüğünü karakterize eden bir dizi ek değişken tanıtalım. (2)'yi bir başlangıç ​​noktası olarak alacağız, eşitsizlik kısıtlamalarını yumuşatacağız ve ayrıca en aza indirgenmiş işlevselliğe toplam hata için bir ceza uygulayacağız:

Faktör, bölen bant genişliğini en üst düzeye çıkarmak ve toplam hatayı en aza indirmek arasındaki ilişkiyi ayarlamanıza izin veren bir yöntem ayarlama parametresidir.

Benzer şekilde, Kuhn-Tucker teoremi ile problemi Lagrange fonksiyonunun eyer noktasını bulmaya indirgeriz:

Benzetme yoluyla, bu sorunu eşdeğer bir soruna indirgeyelim:

Pratikte, bir destek vektör makinesi oluşturmak için, genel durumda noktaların iki sınıfa doğrusal olarak ayrılabilirliğini garanti etmek mümkün olmadığından (3) değil, bu problem çözülür. Algoritmanın bu çeşidine yumuşak marjlı SVM algoritması denir, doğrusal olarak ayrılabilir durumda ise sabit marjlı SVM'den bahseder.

Sınıflandırma algoritması için formül (4) korunur, tek fark artık yalnızca nesneleri desteklemekle kalmayıp aynı zamanda kusurlu nesnelerin de sıfırdan farklı değerlere sahip olmasıdır. Bir anlamda bu bir dezavantajdır, çünkü gürültü emisyonları genellikle ihlal edenlerdir ve bunlar üzerine kurulan karar kuralı aslında gürültüye dayanır.

Sabit genellikle kayan kontrol kriterine göre seçilir. Bu, problemin her değer için yeniden çözülmesi gerektiğinden zaman alıcı bir yöntemdir.

Numunenin neredeyse doğrusal olarak ayrılabilir olduğuna inanmak için bir neden varsa ve yalnızca aykırı değerler yanlış sınıflandırılmışsa, aykırı değer filtrelemesi uygulanabilir. İlk olarak, bazı C için problem çözülür ve en büyük hata değerine sahip nesnelerin küçük bir kısmı örnekten çıkarılır. Bundan sonra, kesilen numune kullanılarak problem tekrar çözülür. Kalan nesneler doğrusal olarak ayrılabilir olana kadar bu yinelemelerin birkaçından geçmeniz gerekebilir.

Vladimir Vapnik ve Alexei Chervonenkis tarafından 1963'te önerilen optimal bölen hiperdüzlemi oluşturmak için algoritma doğrusal bir sınıflandırma algoritmasıdır. Bununla birlikte, 1992'de Bernhard Boser, Isabelle Guyon ve Vapnik, skaler ürünlerden keyfi çekirdeklere geçişe dayalı doğrusal olmayan bir sınıflandırıcı oluşturmak için bir yöntem önerdiler, sözde çekirdek hilesi (ilk olarak M.A. Aizerman, E.M. Bravermann ve L.V. Rozonoer, potansiyel fonksiyonlar yöntemi için), bu da doğrusal olmayan ayırıcılar oluşturmaya izin verir. Ortaya çıkan algoritma, doğrusal sınıflandırma algoritmasına çok benzer, tek fark, yukarıdaki formüllerdeki her nokta çarpımının doğrusal olmayan bir çekirdek işlevi (daha yüksek boyutlu bir uzayda nokta çarpımı) ile değiştirilmesidir. Optimal bir bölen hiperdüzlem bu uzayda zaten mevcut olabilir. Ortaya çıkan uzayın boyutu orijinal olanın boyutundan daha büyük olabileceğinden, skaler ürünleri karşılaştıran dönüşüm doğrusal olmayacaktır, bu da orijinal uzayda optimal bölme hiperdüzlemine karşılık gelen fonksiyonun da doğrusal olmayacağı anlamına gelir.

Orijinal uzay yeterince yüksek bir boyuta sahipse, numunenin içinde lineer olarak bölünebileceğini umabiliriz.

En yaygın çekirdekler şunlardır:

1. Doğrusal çekirdek:

2. Polinom (homojen):

3. RBF işlevi:

4. Sigmoid:

Bize yöneltilen problem çerçevesinde doğrusal homojen bir çekirdek kullanacağız. Bu çekirdek gösterdi mükemmel sonuçlar Belge Sınıflandırma görevlerinde, Naive Bayesian Sınıflandırıcı ile karşılaştırıldığında, bu sınıflandırıcının eğitimi nispeten uzun zaman alır. Bu listedeki diğer tüm çekirdeklerin çalışması da kontrol edildi ve eğitimlerinin çok daha uzun zaman aldığı ve sınıflandırma doğruluğunda özel iyileştirmeler getirmediği bulundu.

Öğrenmeyi hızlandırmak için, doğruluktan çok fazla ödün vermeden sınıflandırıcının eğitimini önemli ölçüde hızlandırmamızı sağlayan Stokastik Gradyan İniş adlı bir yöntem kullanacağız.

Stokastik Gradyan İniş

Gradyan yöntemleri, yalnızca makine öğreniminde kullanılan geniş bir optimizasyon algoritmaları sınıfıdır. Burada, gradyan yaklaşımı, sinaptik ağırlıkların vektörünü doğrusal bir sınıflandırıcıya uydurmak için bir yöntem olarak ele alınacaktır. Yalnızca eğitim setinin nesnelerinde bilinen hedef bağımlılık olsun:

Bağımlılığa yaklaşan bir algoritma bulalım. Doğrusal bir sınıflandırıcı durumunda, istenen algoritma şu şekildedir:

aktivasyon fonksiyonunun rolünü oynadığı yer (en basit durumda, koyabilirsiniz).

Ampirik riski en aza indirme ilkesine göre, bunun için optimizasyon problemini çözmek yeterlidir:

Verilen kayıp fonksiyonu nerede.

Minimize etmek için gradyan iniş yöntemini uygulayın. Bu, vektörün işlevseldeki en büyük düşüş yönünde (yani, antigradyan yönünde) değiştiği her yinelemede adım adım bir algoritmadır:

Öğrenme oranı olarak adlandırılan pozitif bir parametre nerede.

Gradyan iniş uygulamak için 2 ana yaklaşım vardır:

1. Batch, her yinelemede eğitim örneğinin tamamı görüntülendiğinde ve yalnızca bundan sonra değiştirilir. Bu hesaplama açısından pahalıdır.

2. Stokastik (rastgele / çevrimiçi), algoritmanın her yinelemesinde eğitim örneğinden bir (rastgele) şekilde yalnızca bir nesne seçildiğinde. Böylece vektör, yeni seçilen her nesne için ayarlanır.

Stokastik gradyan iniş algoritmasını sözde kodda aşağıdaki gibi temsil edebilirsiniz:

- eğitim örneği

- öğrenme hızı

- fonksiyonel yumuşatma parametresi

1. Ağırlıkların vektörü

1) Ağırlıkları başlat

2) İşlevselliğin mevcut değerlendirmesini başlatın:

3) Tekrar edin:

1. Rastgele bir nesne seçin

2. Algoritmanın çıkış değerini ve hatayı hesaplayın:

3. Degrade iniş adımı yapın

4. İşlevin değerini tahmin edin:

4) Değer sabitlenene ve/veya ağırlıkların değişmesi durana kadar.

SGD'nin ana avantajı, fazladan büyük veriler üzerinde eğitim hızıdır. Önümüze konulan görev çerçevesinde bizim için ilginç olan da bu, çünkü girdi verisi miktarı çok büyük olacak. Aynı zamanda, SGD algoritması, klasik toplu gradyan inişinin aksine, biraz daha düşük sınıflandırma doğruluğu sağlar. Ayrıca, SGD algoritması, doğrusal olmayan bir çekirdeğe sahip bir destek vektör makinesini eğitmek için geçerli değildir.

sonuçlar

Çözülmekte olan problemin bir parçası olarak, nadir olayların ağırlığını arttırmamıza ve sık görülen olayların ağırlığını azaltmamıza izin verecek olan TF-IDF kaynak veri dönüştürme algoritmasını kullanmamız gerekiyor. Dönüşümden sonra elde edilen verileri, karşılaştığımız problemin çözümüne uygun sınıflandırıcılara aktaracağız: Naive Bayesian Sınıflandırıcı veya Doğrusal Çekirdekli Destek Vektör Makinesi, stokastik gradyan iniş yöntemi kullanılarak eğitilmiş. Ayrıca, toplu gradyan inişinde eğitilmiş doğrusal olmayan çekirdeklere sahip bir Destek Vektör Makinesinin performansını test edeceğiz. Fakat, verilen tip sınıflandırıcı, çok karmaşık bir çekirdek ve sınıflandırıcının sınıflandırıcıyı eğitmek için kullanılmayan verilerle iyi başa çıkamadığı yeniden eğitilebilirlik eğilimi nedeniyle eldeki görev için uygun görünmüyor.

verilen yazılım makine ön işlemesi

Yani, bir evin büyüklüğüne göre değeri gibi bir değeri tahmin etme göreviniz var. Veya bir talebin sisteminiz tarafından işleme alınma süresi. Ama ne olduğunu asla bilemezsin.

Doğrusal regresyon kullanmaya karar verdiniz ve şimdi modelinizin öngördüğü fiyat ile satılan evlerin gerçek değeri arasındaki farkın minimum olacağı katsayıları bulmak istiyorsunuz. Bunu yapmak için şu yöntemlerden birini kullanabilirsiniz:

1. Toplu Gradyan İniş
2. Stokastik Gradyan İniş
3. Normal Denklemler
4. Newton'un Yöntemi

Bugün iki tür gradyan inişi hakkında konuşacağız.

Dereceli alçalma

Yine de gradyan inişi nedir?

Bir değişkenden bir tür karmaşık fonksiyon hayal edin. Bazı iniş çıkışları var. Bu fonksiyonun her noktasında türev alabiliriz:

Yeşil çizgi, bu noktada türevin pozitif, kırmızı - negatif olacağını gösteriyor.

Fonksiyondaki herhangi bir noktayı seçin. Bu noktaya en yakın minimuma "aşağı inmek" istiyorsunuz. Noktanızdaki türev pozitifse (yeşil çizgi), bu, minimumun "arkanızda" olduğu ve ona inmek için noktanızın koordinatından çıkarmanız gerektiği anlamına gelir. x türevinizin değeri.

Sizin noktada türev negatifse (kırmızı çizgi), bu, minimumun “önünüzde” olduğu ve ona ulaşmak için tekrar koordinattan çıkarmanız gerektiği anlamına gelir. x türevinizin değeri. Değeri negatiftir ve bu nedenle negatif bir değer çıkararak koordinatı artıracaksınız. x.

Pekala, inişin dayanılmaz derecede uzun veya hatalı bir şekilde hızlı olmaması için, seçilen noktadaki türevinizin değerini bir faktörle çarpın.

Ancak bu, işlevin bir koordinata bağlı olduğu durumlarda geçerlidir. Ev satma modelimizde, maliyet fonksiyonu iki değişkene bağlıdır.

Bu işlevi 3B uzayda bir "bardak" olarak düşünebilirsiniz:

Birkaç değişkenli fonksiyonların türevine gradyan denir. Gradyan, vektörün her bir öğesinin bir değişkenin türevi olduğu, değişken sayısı boyutuna sahip bir vektördür.

Maliyet fonksiyonumuz:

Gradyan olarak belirtilir ve aşağıdaki formülle hesaplanacaktır:

Her kısmi türevde, onu bir değişkenden sayarız. Diğer tüm değişkenler sabit olarak kabul edilir, bu nedenle türevleri sıfıra eşit olacaktır:

Bundan sonra, aşağıdaki formülü kullanarak her değeri güncelleriz:

Parametreye öğrenme oranı denir ve fonksiyonun minimum değerine ne kadar hızlı hareket edeceğimizi belirler. Parametrelerin her güncellemesinde minimuma doğru küçük bir adım atıyoruz. Bundan sonra prosedürü tekrarlıyoruz. Buna paralel olarak bir önceki adıma göre maliyet fonksiyonunun değerinin ne kadar değiştiğine bakıyoruz. Bu değişiklik çok küçüldüğünde (zamanı işaretliyoruz) durabilir ve minimum noktaya ulaştığımızı varsayabiliriz.

En yakın çukura doğru bir tepeden inmek gibidir. Gradyan iniş, yerel minimumu bulmanızı sağlar, ancak global olanı değil. Bu, işlevinizin minimum düzeyde olduğu birkaç nokta varsa, eğim inişinin sizi bunlardan birine götüreceği anlamına gelir - başlangıç ​​noktasına en yakın olan, ancak en derin yarık olması gerekmez.

İlk adımdan önce, parametreleri rastgele bir şekilde belirliyoruz ve elde edeceğimiz tam minimum, onları nasıl tanımladığımıza bağlı:

Burada parantez içinde not edilmelidir ki, yukarıdaki gradyan inişiyle ilgilidir. Genel görünüm ancak özellikle için gradyan inişi ile ilgilenmez doğrusal regresyon... Doğrusal regresyon maliyet işlevi dışbükeydir ve yalnızca bir minimuma sahiptir (3B bir kap düşünün), bu nedenle gradyan inişi her zaman onu bulacaktır.

Maliyet fonksiyonunun minimum değerine ne kadar yaklaşırsanız (tahmin edilen fiyat ile gerçek fiyat arasındaki fark ne kadar küçükse), satırınız geçmiş verilerinizi o kadar iyi tanımlar:

Çok fazla tarihsel örnek olmadığında her şey yolundadır, ancak milyonlarcası olduğunda, minimuma her küçük adım için milyonlarca hesaplama yapmak zorundayız ve bu uzun zaman alabilir.

Buna bir alternatif, stokastik gradyan inişi olabilir - bir örnek alıp değerleri güncellediğimiz, yalnızca ona odaklandığımız bir yöntem. Ardından bir sonraki örneği alıp parametreleri güncelleyerek ona odaklanıyoruz. Vb. Bu, tepeden her zaman "aşağı inmememize", bazen bir adım yukarı veya yana doğru gitmemize, ancak er ya da geç bu minimuma ulaşıp etrafında dönmeye başladığımıza yol açar. Değerler bize uymaya başlayınca (ihtiyacımız olan doğruluğa ulaşınca) inişi durduruyoruz.

Sözde kodda, stokastik gradyan inişi şöyle görünür:

Maliyet Fonksiyonu değişikliği küçük olana kadar: (

j için: = 1 ila m (

Son olarak, algoritmanın yakınsama özellikleri: Yeterince küçük bir değer kullanılması koşuluyla toplu gradyan inişi her zaman minimuma yakınsar. Stokastik gradyan inişi genellikle minimuma yakınsar, ancak yakınsamanın elde edilmesini sağlayan modifikasyonlar vardır.

Stokastik gradyan şu formülle tahmin edilir:

yani verilen rasgele yönlerde minimize edilecek fonksiyonun artışlarına eşit ağırlıklara sahip tüm rasgele vektörlerin toplamıdır.

Birim vektörleri birim vektörler olarak alırsak, yani (3.3.22'den kolayca görülebileceği gibi) için bu tahmin, gradyanın tam değerini verir.

Tanımlanan gradyan tahminlerinin her ikisi de, deterministik tahmin yönteminden (3.3.22) önemli ölçüde farklı oldukları dahil olmak üzere herhangi bir değer için etkili bir şekilde uygulanabilir; bunun için kesinlikle aynı durum, deterministik yöntemlerin rastgele tarafından genelleştirildiğini doğrular (sonuna bakın). alt bölüm 3.3.1). Böyle bir genellemeye bir örnek daha verelim.

Gradyan araması (3.3.21), en az iki rastgele arama algoritmasının özel bir durumudur. İlk algoritma:

nerede hala bir birim rasgele boyutlu vektör. İyi bilinen bir gradyan rastgele arama algoritmasıdır. İkinci algoritma forma (3.3.23) sahiptir, ancak gradyan tahmini formülle hesaplanır.

Görülmesi kolay olduğu gibi, her iki algoritma da bir gradyan arama algoritmasına (3.3.21) dönüşmektedir.

Bu nedenle rastgele arama, bilinen düzenli arama yöntemlerinin doğal bir uzantısı, devamı ve genelleştirilmesidir.

Açılan başka bir rastgele arama özelliği bol fırsatlar etkin uygulaması için, optimize edilmiş parametreler alanında arama yönlerini bulmak için karmaşık düzenli operatörlerin stokastik bir modeli olarak rastgele adım operatörünün kullanılmasıdır.

Bu nedenle, doğrusal taktiklere sahip rastgele arama algoritması (3.3.12), en dik iniş algoritmasının stokastik bir modelidir:

rastgele bir vektörün gradyan tahminini simüle ettiği. Böyle bir "tahmin"in, stokastik özellikleri, tahmin edilen gradyanın özelliklerine bile benzemediğinden, ham olarak adlandırılamaması ilginçtir. Bununla birlikte, yukarıda gösterildiği gibi, rastgele arama algoritması sadece verimli olmakla kalmaz, aynı zamanda bazı durumlarda en dik iniş algoritmasından daha verimlidir. Burada

rasgele adım operatörü, örneğin formül (3.3.22)'ye göre hantal gradyan tahmin operatörünün yerini alır.

Rastgele aramanın onu normal yöntemlerden olumlu bir şekilde ayıran bir sonraki özelliği, kendisini öncelikle küresel bir ekstremum bulmak için tasarlanmamış yerel rastgele arama algoritmalarında gösteren küreselliktir. Böylece, rastgele iniş algoritması global bir ekstremum bulabilirken, normal en dik iniş algoritması, prensipte, yerel bir ekstremum bulmak için inşa edildiğinden böyle bir olasılığa izin vermez.

Sonuç olarak, rastgele arama algoritmalarının küreselliği, rastgelelik kullanımı için bir "bonus" ve "gibi bir şey" gibidir. ücretsiz uygulama»Algoritmaya. Bu durum, özellikle bilinmeyen bir yapıya sahip nesneleri optimize ederken, sorunun tek uç noktasına tam bir güven olmadığında ve birkaç uç noktanın varlığının mümkün olduğu durumlarda (beklenmese de) önemlidir. Bu durumda küresel arama yöntemlerini kullanmak akılsızca savurganlık olur. Yerel rastgele arama yöntemleri, yerel bir sorunu etkin bir şekilde çözdükleri ve ilke olarak, varsa küresel bir sorunu çözebildikleri için burada en kabul edilebilir olanıdır. Bu, kullanıcıların çok değer verdiği bir tür psikolojik güvenilirliğe sahip rastgele aramalar sağlar.

Rastgele aramanın algoritmik basitliği, onu öncelikle tüketiciler için çekici kılar. Deneyimler, iyi bilinen rastgele arama algoritmalarının, her bir özel durumda, kullanıcının sadece zevklerini ve eğilimlerini (göz ardı edilemez) değil, aynı zamanda özelliklerini de yansıtan yeni algoritmaların "modellerini işlediği" bir "tuval" olduğunu göstermektedir. optimize edilen nesnenin İkincisi, algoritmanın "nesne için" tasarlanması gerektiğine dair iyi bilinen ilkenin uygulanması için uygun bir temel oluşturur. Son olarak, rastgele aramanın algoritmik basitliği, donanım uygulamasının basitliğini belirler. Bu, yalnızca sınırsız sayıda optimize edilebilir parametreye sahip basit, kompakt ve güvenilir optimize ediciler oluşturmayı mümkün kılmakla kalmaz, aynı zamanda optimal sentezlerini bir bilgisayarda oldukça basit bir şekilde düzenlemeyi mümkün kılar.

Dereceli alçalma En çok kullanılan öğrenme algoritmasıdır, hemen hemen her modelde kullanılmaktadır. Gradyan inişi, temel olarak modellerin nasıl eğitildiğidir. GE olmasaydı, makine öğrenimi bugün olduğu yerde olmazdı. Bazı modifikasyonlarla gradyan iniş yöntemi, eğitim ve derin için yaygın olarak kullanılır ve hatalar olarak bilinir.

Bu yazıda, biraz matematikle gradyan inişinin bir açıklamasını bulacaksınız. Özet:

• HS'nin amacı, tüm algoritmayı açıklamaktır;
• Algoritmanın çeşitli varyasyonları;
• Kod uygulaması: Phyton dilinde kod yazma.

gradyan inişi nedir

Gradyan iniş, bir kayıp fonksiyonunun minimum değerini bulmak için bir yöntemdir (bu fonksiyonun birçok türü vardır). Herhangi bir özelliği en aza indirmek, o özellikteki en derin vadiyi aramak anlamına gelir. İşlevin, bir makine öğrenimi modelinin tahminlerindeki hatayı kontrol etmek için kullanıldığını unutmayın. Minimumu bulmak, mümkün olan en küçük hatayı almak veya modelin doğruluğunu artırmak anlamına gelir. Modelimizin parametrelerini (ağırlıklar ve önyargılar) ayarlarken eğitim veri kümesini yineleyerek doğruluğu artırıyoruz.

Bu nedenle, kayıp fonksiyonunu en aza indirmek için gradyan inişi gereklidir.

Algoritmanın özü, en küçük hata değerini elde etme işlemidir. Aynı şekilde, vadinin dibinde (en düşük hata değeri) altın bulmak amacıyla bir çukura inmek olarak görülebilir.

Bir fonksiyonun minimumunu bulma

Ayrıca, kayıp fonksiyonunda (bir ağırlığa göre) en düşük hatayı (en derin dip) bulmak için model parametrelerini ayarlamanız gerekir. Onları nasıl kurarız? Bu matematiksel analize yardımcı olacaktır. Analiz sayesinde, bir fonksiyonun grafiğinin eğiminin, fonksiyonun değişkene göre türevi olduğunu biliyoruz. Bu eğim her zaman en yakın çukuru gösterir!

Şekilde, bir ağırlıkla kayıp fonksiyonunun ("J" sembolü ile "Hata" olarak adlandırılan) bir grafiğini görüyoruz. Şimdi kayıp fonksiyonunun eğimini (dj/dw diyelim) bir ağırlığa göre hesaplarsak, yerel minimuma ulaşmak için hareket etmemiz gereken yönü elde ederiz. Şimdilik modelimizin sadece bir ağırlığı olduğunu varsayalım.

kayıp fonksiyonu

Önemli: tüm antrenman verileri üzerinde yinelediğimiz gibi, her ağırlık için dJ/dw değerleri eklemeye devam ediyoruz. Kayıp eğitim örneğine bağlı olduğu için dJ/dw de değişmeye devam ediyor. Daha sonra ortalamayı elde etmek için toplanan değerleri eğitim örneklerinin sayısına böleriz. Daha sonra her bir ağırlığı ayarlamak için bu ortalamayı (her ağırlığın) kullanırız.

Ayrıca not edin: Kayıp işlevi, her eğitim örneğindeki hatayı izlemek için tasarlanmıştır, bu eğitim örneğinde göreli bir ağırlık işlevinin türevi, ağırlığın en aza indirilmesi için kaydırılması gereken yerdir. Kayıp işlevini kullanmadan bile modeller oluşturabilirsiniz. Ama her ağırlığa (dJ/dw) göre türevi kullanmanız gerekir.

Artık ağırlığı hangi yöne iteceğimizi belirlediğimize göre, bunu nasıl yapacağımızı bulmamız gerekiyor. Burada hiper parametre olarak adlandırılan bir öğrenme oranı faktörü kullanıyoruz. Hiper parametre, modeliniz için gerekli olan ve hakkında gerçekten çok belirsiz bir fikre sahip olduğumuz bir değerdir. Genellikle bu değerler deneme yanılma yoluyla öğrenilebilir. Burada öyle değil: biri tüm hiper parametrelere uyar. Öğrenme oranı faktörü, yönün dJ/dw'den geldiği "doğru yönde atılan bir adım" olarak düşünülebilir.

Tek bir kilo verme işleviydi. Gerçek bir modelde, tüm eğitim örneklerini yineleyerek, tüm ağırlıklar için yukarıdakilerin hepsini yaparız. Nispeten küçük bir makine öğrenimi modelinde bile 1 veya 2'den fazla ağırlığınız olacaktır. Bu, grafiğin zihnin hayal edemeyeceği boyutlara sahip olacağı için görselleştirmeyi zorlaştırır.

Gradyanlar hakkında daha fazla bilgi

Kayıp fonksiyonuna ek olarak, gradyan inişi ayrıca dJ / dw (tüm ağırlıklar için gerçekleştirilen kayıp fonksiyonunun bir ağırlığa göre türevi) olan bir gradyan gerektirir. DJ / dw kayıp fonksiyonu seçiminize bağlıdır. En yaygın kayıp işlevi, kök ortalama kare hatasıdır.

Bu fonksiyonun herhangi bir ağırlığa göre türevi (bu formül, gradyanın hesaplanmasını gösterir):

GE'deki tüm matematik budur. Buna bakarak diyebiliriz ki, aslında GE çok fazla matematik içermiyor. İçerdiği tek matematik, elde edeceğimiz çarpma ve bölmedir. Bu, işlev seçiminizin her ağırlığın gradyanının hesaplanmasını etkileyeceği anlamına gelir.

Öğrenme oranı oranı

Yukarıda yazılanların hepsi ders kitabında var. Gradyan inişiyle ilgili herhangi bir kitabı açabilirsiniz, aynı şeyi söyleyecektir. Her kayıp işlevi için gradyan formülleri, bunları kendiniz nasıl türeteceğinizi bilmeden İnternette bulunabilir.

Bununla birlikte, çoğu modeldeki sorun, öğrenme oranı faktörü ile ortaya çıkar. Her ağırlık için güncellenmiş ifadeye bir göz atalım (j, 0'dan ağırlık sayısına kadar değişir ve Theta-j j. ağırlık ağırlık vektöründe, k, 0'dan ofset sayısına kadar değişir; burada B-k, ofset vektöründeki k'inci ofsettir). Burada alfa öğrenme oranı faktörüdür. Buradan dJ / dTheta-j (ağırlık gradyanı Theta-j) ve ardından alfa boyutunun o yöndeki adımını hesapladığımızı söyleyebiliriz. Bu nedenle, yokuş aşağı gidiyoruz. Ofseti güncellemek için Theta-j'yi B-k ile değiştirin.

Bu adım boyutu alfa çok büyükse, minimumun üstesinden geleceğiz: yani minimumu kaçıracağız. Alfa çok küçükse, minimuma ulaşmak için çok fazla yineleme kullanırız. Yani alfa iyi olmalı.

Gradyan inişini kullanma

Pekala, hepsi bu. Gradyan inişi hakkında bilinmesi gereken tek şey bu. Her şeyi sözde kodda özetleyelim.

Not: Ölçekler burada vektörler halinde sunulmuştur. Daha büyük modellerde, muhtemelen matrisler olacaktır.

i = 0'dan "eğitim örneği sayısı"na

1. Her ağırlık ve sapma için i-inci eğitim örneği için kayıp fonksiyonunun gradyanını hesaplayın. Artık her ağırlık için gradyanlarla dolu bir vektörünüz ve ofset gradyanı içeren bir değişkeniniz var.

2. Tek bir birikimli vektör için hesaplanan ağırlık gradyanlarını ekleyin; bu, siz her bir vaka çalışmasını yineledikten sonra, birkaç yinelemede her bir ağırlığın gradyanlarının toplamını içermelidir.

3. Ağırlıklarla ilgili duruma benzer şekilde, birikimli değişkene bir sapma gradyanı ekleyin.

Şimdi, tüm eğitim örneklerini yineledikten SONRA aşağıdakileri yapın:

1. Ağırlıkların ve önyargıların birikimli değişkenlerini eğitim örneklerinin sayısına bölün. Bu bize tüm ağırlıklar için ortalama gradyanları ve ofset için ortalama gradyanı verecektir. Bunlara yenilenmiş akümülatörler (OA) diyelim.

2. Ardından, aşağıdaki formülü kullanarak tüm ağırlıkları ve sapmaları güncelleyin. DJ / dTheta-j yerine, ağırlıklar için OA'yı ve sapma için OA'yı kullanacaksınız. Ofset için de aynısını yapın.

Bu, gradyan inişinin yalnızca bir yinelemesiydi.

Bir dizi yineleme için bu işlemi baştan sona tekrarlayın. Bu, GS'nin 1. yinelemesi için tüm eğitim örneklerini yinelediğiniz, degradeleri hesapladığınız ve ardından ağırlıkları ve önyargıları güncellediğiniz anlamına gelir. Sonra bunu birkaç GE yinelemesi için yaparsınız.

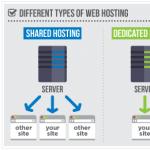
Farklı gradyan iniş türleri

Degrade iniş için 3 seçenek vardır:

1. Mini toplu: burada, tüm eğitim örneklerini gözden geçirmek ve her yinelemede yalnızca bir eğitim örneğinde hesaplamalar yapmak yerine, aynı anda n eğitim örneğini işliyoruz. Bu seçim çok büyük veri kümeleri için iyidir.

2.Stokastik Gradyan İniş: bu durumda, her öğrenme örneğini kullanmak ve döngüye almak yerine SADECE BİR KEZ KULLANIYORUZ. Dikkat edilmesi gereken birkaç şey var:

• HS'nin her yinelemesinde, eğitim setini karıştırmanız ve rastgele bir eğitim örneği seçmeniz gerekir.
• Yalnızca bir eğitim örneği kullandığınız için, yerel minimumlara giden yolunuz çok fazla sarhoş olan sarhoş bir kişi gibi çok gürültülü olacaktır.

3. GS serisi: önceki bölümlerde yazılanlar bunlardı. Her eğitim örneğinde dolaşın.

3 isabeti yerel düşüşlerle karşılaştıran resim

Örnek piton kodu

GS serisine uygulandığında, bir Python eğitim kodu bloğu böyle görünür.

Def tren (X, y, W, B, alpha, max_iters): "" "Tüm eğitim örneklerinde GD gerçekleştirir, X: Eğitim veri seti, y: Eğitim verileri için etiketler, W: Ağırlık vektörü, B: Bias değişkeni, alfa : Öğrenme oranı, max_iters: Maksimum GD yinelemeleri. "" "DW = 0 # Ağırlıklar gradyan akümülatör dB = 0 # Bias gradyan akümülatör m = X.şekil # No. i aralığındaki (max_iters) eğitim örneklerinin sayısı: dW = 0 # (m) aralığındaki j için dB = 0 akümülatörleri sıfırlama: # 1. Tüm örnekleri yineleyin, # 2. w_grad ve b_grad, # 3. w_grad ekleyerek dW'yi güncelleyin ve b_grad ekleyerek dB'yi güncelleyin, W = W - alpha * (dW / m) # Ağırlıkları güncelleyin B = B - alpha * (dB / m) # Sapma dönüşünü güncelleyin W, B # Güncellenmiş ağırlıkları ve önyargıyı döndürün.

Bu kadar. Artık gradyan inişinin ne olduğunu iyi anlamalısınız.

nerede F i - i. partide hesaplanan fonksiyon, i rastgele seçilir;

Öğrenme adımı bir hiper parametredir; değerler çok büyükse öğrenme algoritması uzaklaşacak, çok küçükse yavaş yakınsayacaktır.

Ataletli stokastik gradyan inişi

Stokastik gradyan inişi yönteminde, gradyanın her yinelemede büyük ölçüde değişmesi alışılmadık bir durum değildir. Bunun nedeni, işlevselliğin önemli ölçüde farklılık gösterebilecek çeşitli veriler üzerinde hesaplanmasıdır. Bu değişiklik, önceki yinelemelerde hesaplanan ve eylemsizlik hiperparametresi μ tarafından ölçeklenen gradyanlar kullanılarak düzeltilebilir:

	(14)
	(15)

Tahmin edebileceğiniz gibi, eylemsizlik hiperparametresi μ, Newton'un sözde eylemsizlik kuvveti gibi, yani. reaksiyon kuvveti, gradyandaki değişikliklere "direnir" ve eğitim sırasında ağırlık katsayılarındaki değişiklikleri yumuşatır. Bu öğrenme algoritmasına momentum veya SGDM ile stokastik gradyan inişi denir.

Uyarlanabilir gradyan yöntemi

Uyarlanabilir gradyan algoritması (Adagrad), ölçeklendirme fikrine dayanmaktadır. Bu parametre için tüm geçmiş gradyanların geçmişini hesaba katarken, her ayarlanabilir parametre için öğrenme oranını ayrı ayrı yeniden ölçeklendirir. Bunu yapmak için, her bir degrade öğesi, önceki karşılık gelen degrade öğelerinin karelerinin toplamının kareköküne bölünür. Bu yaklaşım, büyük bir gradyan değerine sahip olan ağırlıklar için öğrenme oranını etkili bir şekilde azaltır ve ayrıca her yinelemede tüm parametreler için karelerin toplamı sürekli olarak arttığından, tüm parametreler için zamanla öğrenme oranını azaltır. Sıfır başlangıç ​​ölçekleme parametresi g = 0 ayarlanırken, ağırlık katsayılarını yeniden hesaplama formülü şu şekildedir (bölme eleman eleman yapılır).