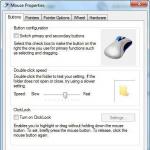
Berechnungsschema. „VBA-Algorithmusentwicklung. Blockdiagramm. Algorithmusstrukturen. Eingabe- und Ausgabeoperatoren in der Programmiersprache Pascal

Der Alltag eines jeden Menschen besteht aus der Lösung einer Vielzahl unterschiedlich komplexer Aufgaben im Beruf oder im Studium. Manche Aufgaben sind so einfach, dass wir bei der Ausführung bestimmte Aktionen automatisch ausführen, ohne darüber nachzudenken. Die Lösung eines jeden Problems, auch des einfachsten, erfolgt in der Regel sukzessive in mehreren Schritten. Eine solche Reihenfolge beim Lösen von Problemen wird als Algorithmus bezeichnet. Heute schauen wir uns an, was lineare Algorithmen sind, wie ihre Struktur dargestellt wird, wie sie gelöst und programmiert werden.

Algorithmensprache

Bei diesem Konzept handelt es sich um eine genaue Anweisung an den Ausführenden, eine bestimmte Handlungsfolge auszuführen, die auf die Lösung der Aufgabe abzielt.

Diese Sprache ist ein Mittel zur Beschreibung von Algorithmen, die in der Regel benutzerorientiert sind.

• Start-End-Block des Algorithmus. Auf dem Block befindet sich die Aufschrift „Anfang“ oder „Ende“.
• Dateneingabe-/-ausgabeblock. Dieser Block wird als Parallelogramm dargestellt. Darauf sind folgende Aufschriften angebracht: „Eingabe“, „Ausgabe“, „Drucken“. Sie werden außerdem von einer Liste von Eingabe- oder Ausgabevariablen begleitet.
• Arithmetischer Block oder Entscheidungsblock. Es entspricht einem Rechteck. Der Block sollte die Aufschrift „Operation“, „Gruppe von Operationen“ haben.

Mit Hilfe solcher Blockdiagramme wird die Lösung linearer Algorithmen dargestellt. Lassen Sie uns als Nächstes über die Funktionen der Wertezuweisung sprechen.

Lineare Rechenalgorithmen

Die wichtigste Elementaraktion in einem Rechenalgorithmus besteht darin, einer Variablen einen bestimmten Wert zuzuweisen. Wenn der Wert einer Konstanten durch die Art ihrer Notation bestimmt wird, erhält der Variablenwert allein durch die Zuweisung einen bestimmten Wert. Dies kann auf zwei Arten erfolgen: mit dem Zuweisungsbefehl; mit dem Eingabebefehl.

Ein Beispiel für eine lineare Algorithmuslösung

Geben wir ein Beispiel für eine Beschreibung der Regeln zum Teilen gewöhnlicher Brüche mit einem linearen Algorithmus, die in Schulbüchern folgenden Inhalt haben:

• der Zähler von Bruch 1 muss mit dem Nenner von Bruch 2 multipliziert werden;
• der Nenner von Bruch 1 muss mit dem Zähler von Bruch 2 multipliziert werden;
• Sie müssen einen Bruch aufschreiben, bei dem der Zähler das Ergebnis der Vervollständigung von 1 Punkt und der Nenner das Ergebnis der Vervollständigung von 2 Punkten ist. Die algebraische Form dieser Regel lautet wie folgt:

a/b: c/d=(a*d)/(b*d)=m/n.

Erstellen wir also einen Algorithmus zum Teilen von Brüchen für einen Computer. Um Verwirrung zu vermeiden, verwenden wir für Variablen die gleiche Notation wie in der oben angegebenen Formel. a, b, c, d – Quelldaten in Form von Ganzzahlvariablen. Das Ergebnis sind ebenfalls ganzzahlige Werte. Die Lösung in algorithmischer Sprache lautet wie folgt:

alg Division von Brüchen

intakt a, b, c, d, m, n

Geben Sie a, b, c, d ein

con

Grafische Darstellung der Lösung

Das Diagramm des oben beschriebenen linearen Algorithmus sieht folgendermaßen aus:

Der Wertzuweisungsbefehl hat das folgende Format:

Variable:=Ausdruck.

Das „:=“-Zeichen wird als Zuweisen gelesen.

Zuweisung ist ein Befehl, der für den Computer erforderlich ist, um die folgenden Aktionen auszuführen:

• Ausdrucksberechnungen;
• Zuweisen des resultierenden Werts zu einer Variablen.

Der obige Algorithmus enthält zwei Befehle als Zuweisung. In einem Blockdiagramm muss die Zuweisungsanweisung in ein Rechteck geschrieben werden, das als Berechnungsblock bezeichnet wird.

Bei der Beschreibung linearer Algorithmen besteht keine besondere Notwendigkeit, beim Schreiben von Ausdrücken strenge Regeln einzuhalten. Sie können sie in der üblichen mathematischen Form schreiben. Schließlich handelt es sich hierbei nicht um die strenge Syntax einer Programmiersprache.

Im angegebenen Beispielalgorithmus gibt es auch einen Eingabebefehl:

Geben Sie a, b, c, d ein.

Der Eingabebefehl in einem Blockdiagramm wird in einem Parallelogramm geschrieben, also in einem Eingabe-Ausgabe-Block. Durch die Ausführung dieses Befehls unterbricht der Prozessor den Betrieb, bis der Benutzer bestimmte Aktionen ausführt. Nämlich: Der Benutzer muss die Eingabevariablen (ihre Werte) auf der (Tastatur) eingeben und die Eingabetaste drücken, die als Eingabetaste fungiert. Es ist wichtig, dass die Werte in derselben Reihenfolge eingegeben werden wie die entsprechenden Variablen, die sich in der Eingabeliste befinden.

Linearer Algorithmus. Seine Programmierung

Wie am Anfang des Artikels erwähnt, können lineare Programme die folgenden Anweisungen enthalten:

• Abtretung;
• Eingang;
• Abschluss.

Das heißt, unter Verwendung der aufgeführten Operatoren werden Algorithmen implementiert.

In der Programmiersprache wird es also so geschrieben:

LET A = B, wobei A eine Variable und B ein Ausdruck ist. Beispiel: A = Y + 20.

Die Eingabeanweisung sieht folgendermaßen aus:

INPUT, zum Beispiel: INPUT C

Der Operator zur Ausgabe von Daten, Werten, wird in folgender Form geschrieben:

DRUCKEN. Zum Beispiel PRINT S.

Lassen Sie uns ein einfaches Beispiel geben. Wir müssen ein Programm schreiben, das die Summe der über die Tastatur eingegebenen Zahlen A und B ermittelt.

In einer Programmiersprache erhalten wir ein Programm, dessen Text unten dargestellt ist.

Eingabe- und Ausgabeoperatoren in der Programmiersprache Pascal

Pascal bietet keine speziellen Operatoren zur Angabe der Eingabe- oder Ausgabeoperationen, die lineare Algorithmen verwenden. In Programmen werden Informationen über eingebaute Prozeduren ausgetauscht. Da eine vorläufige Beschreibung der Standardprozedur nicht erforderlich ist, steht sie jedem Programm zur Verfügung, das einen Aufruf dazu enthält. Auch der Name des genannten Verfahrens ist kein reserviertes Wort.

Bei der Dateneingabe werden solche Operatoren verwendet, um auf ein Standard-Dateneingabeverfahren zu verweisen, das bereits in das Programm integriert ist.

Lesen Sie (A, B, C), wobei A, B, C Variablen sind, die zum Speichern in den RAM eingegeben werden müssen.

Readlnn (x1, y, x2) – nach Abschluss der Eingabe bewegt sich der Cursor an den Anfang einer neuen Zeile.

Readlnn; - zeigt an, dass Sie darauf warten, die Eingabetaste zu drücken. Typischerweise wird diese Anweisung vor dem letzten „Ende“ in den Text eingefügt, um die Ergebnisse der Programmausführung auf dem Inhaltsbildschirm zu speichern.

Die Daten werden auf dem Monitorbildschirm mit den folgenden Operatoren angezeigt:

Schreiben (A, B, C) – Durch Angabe der Werte A, B, C in einer Zeile verlässt der Cursor die aktuelle Zeile nicht.

Writeln (z, y, z2) – Nach Abschluss der Ausgabe der Werte bewegt sich der Cursor an dieser Position in eine neue Zeile.

Schreiben; – bedeutet, dass eine Zeile übersprungen und zum Anfang einer neuen Zeile gewechselt wird.

Mit Hilfe solch einfacher Operatoren werden Daten in der Pascal-Sprache ein- und ausgegeben.

Zusammenfassung anderer Vorträge

„Grundlegende algorithmische Strukturen“ – Ausführung von „Loop Body“-Befehlen. Blockdiagramm der algorithmischen Struktur „Verzweigung“. Sei n=5; i=4. Blockdiagramm des zyklischen Algorithmus. Ende. Algorithmische Struktur „Wahl“. Sei n=5; ich=5. Start. Verzweigungsstruktur. Sei n=5; ich=6. Grundtypen algorithmischer Strukturen. Algorithmische Struktur „Zyklus“. Positive Zahl. Flussdiagramm der algorithmischen Struktur „Auswahl“. Blockdiagramm des linearen Algorithmus.

„Arten von Algorithmen“ – Wohnungsreinigung. Öffnen Sie die Tasche. Unterrichtsmotto. Türme von Hanoi. Name der Figur. Sehen Sie sich den Cartoon an. Ernte die Ernte. Einführung in den Algorithmus. Nähern Sie sich der Kreuzung. Zyklische Algorithmen. Betreten Sie den Garten. Palmen. Algorithmus menschlichen Handelns. Grafisches Diktat. Aufnahmealgorithmen. Algorithmus.

Aufzeichnen eines Zyklus in einer Prozedur. Korrektur des Verfahrens. Grundfarben. Lass uns eine Wand zeichnen. Was ist ein Algorithmus? Team. Interaktives Tutorial. Das Dach zeichnen. Lass uns ein Haus zeichnen. Lass uns malen. Wir zeichnen Fenster. Das Haus ist fertig. Zyklus. Wissen. Stiftfarbe ändern.

„Probleme mit linearen Algorithmen“ - X = 0 Es gibt keine Lösungen. Y = 2. X = 3 Y = 1/48. Die Koordinaten der Eckpunkte des Dreiecks ABC sind angegeben. Berechnen Sie den Wert der Y-Funktion bei X=2 mithilfe des Algorithmus-Flussdiagramms. Wandeln Sie A in größere Informationseinheiten um. Unter Algorithmen versteht man den Prozess der Entwicklung eines Algorithmus (Aktionsplans) zur Lösung eines Problems. X = -1 Es gibt keine Lösungen. Beispiele für Problemlösungen. Gegeben sind die Längen der Seiten des Dreiecks A, B, C. Finden Sie die Fläche des Dreiecks S. Erstellen Sie ein Blockdiagramm des Algorithmus zur Lösung des Problems.

„Algorithmische Konstruktionen“ – Eine Methode zur Darstellung von Algorithmen in Form eines Diagramms. Verzweigung. Darstellung von Algorithmen in Form einer Beschreibung einer Handlungsfolge. Darstellungsformen von Algorithmen. Flussdiagramm des „Wallpapering“-Algorithmus. Algorithmische Designs. Algorithmus zur Lösung des Problems. Blockdiagramm. Grafische Darstellung von Algorithmen. Methoden zur Darstellung von Algorithmen. Algorithmus. Komplexer Algorithmus. Blockdiagramme grundlegender Strukturen.

„Haupttypen algorithmischer Strukturen“ – Schreiben Sie Algorithmen in verbaler Form. In Gruppen arbeiten. Struktur. Schreibweise von Präfixen. Grundtypen algorithmischer Strukturen. Überprüfung selbstständiger Arbeit. Körperliche Bewegung. Aufgaben zur Wissensfestigung. Algorithmus. Grundstruktur. Anfangsparameter einstellen. Rezept zur Teezubereitung. Verzweigung. Finden Sie die Wurzel. Schleife mit Nachbedingung. Zyklus. Zeichen blockieren. Ende des Algorithmus. Haupttypen agrorhythmischer Strukturen.

Allgemeine Anweisungen
Zur Synthese der Schaltkreise in Abschn. 5.1 beschreibt die folgenden Schritte:
1. Beschreibung der Funktion der benötigten Schaltung.
2. Zuweisung von Ein- und Ausgangsvariablen und Zuweisung der Werte 0 und 1.
3. Erstellen einer Wahrheitstabelle.
4. Bestimmung der notwendigen logischen Operationen.
5. Vereinfachung und ggf. Umgestaltung der Schaltung.
Wenn die Wahrheitstabelle bekannt ist, empfiehlt es sich nun, die 4. Stufe mit der Erstellung der Normalform von OR zu beginnen. Mithilfe eines Carnot-Diagramms wird es so weit wie möglich vereinfacht. Am Ende von Schritt 4 erhält man eine vereinfachte Logikfunktion, mit der man eine logische Digitalschaltung aufbauen kann.
Schritt 5 prüft, ob eine weitere Vereinfachung der mithilfe der logischen Algebra gefundenen Funktion möglich und sinnvoll ist. Wenn ja, muss eine Vereinfachung vorgenommen werden.
Jetzt müssen wir herausfinden, welche logischen Elemente verfügbar sind. Die logische Funktion muss so konvertiert werden, dass sie nur die verfügbaren logischen Elemente enthält. Dann können Sie die Schaltung zusammenbauen.

Digitale Ein-/Ausschaltung von mehreren Standorten aus

Mithilfe von Logikgattern müssen Sie einen Schaltkreis synthetisieren, der an mehreren Stellen als Ein/Aus-Schaltkreis fungiert. Der Ausgangszustand sollte sich nur ändern, wenn sich der Zustand eines der Eingänge ändert. Wenn beide Eingänge ihren Zustand ändern, sollte sich der Ausgangszustand nicht ändern. Die Schaltung muss auf ODER-NICHT-Elementen aufgebaut sein.
Die gewünschte Schaltung hat zwei Eingänge und einen Ausgang. Die Eingabevariablen heißen A und B. Die Ausgabevariable heißt Z (Abbildung 5.47).
Die Wahrheitstabelle einer Schaltung mit zwei Eingangsvariablen hat 4 Möglichkeiten (Abb. 5.48). Der Anfangszustand Z für die erste Option kann beliebig eingestellt werden. Ausgewähltes Z = 0.
Beim Übergang von Option 1 zu Option 2 ändert Variable A ihren Zustand. Variable B ändert den Zustand nicht. Wenn nur einer der Eingänge seinen Zustand ändert, muss entsprechend der gestellten Aufgabe der Ausgang Z seinen Zustand ändern. Z muss gleich 1 sein.
Beim Übergang von Option 2 zu Option 3 ändern die Variablen A und B ihren Status. Z sollte sich nicht ändern. Beim Übergang von Option 3 zu Option 4 ändert Variable A ihren Zustand von 0 auf 1. B bleibt gleich 1. Daher muss Z seinen Zustand von 1 auf 0 ändern. Die Wahrheitstabelle ist fertig. Es könnte anders aussehen, wenn wir in Option 1 Z=1 gewählt hätten.
Für die Wahrheitstabelle (Abb. 5.48) müssen Sie die Normalform OR aufschreiben. Es sieht aus wie das:
Z = (AaB)w(AaB).
Wenn man in das Carnot-Diagramm die Normalform OR einträgt, sieht man, dass eine weitere Vereinfachung nicht möglich ist (Abb. 5.49).
Da die Schaltung auf OR-HE-Elementen aufgebaut sein muss, ist es notwendig, die Gleichungen umzuwandeln:
Z = (AaB)w(AaB)-,
Z = (AaB)v(AaB),
Z = AaBaAaB.

Reis. 5,50 Digitalschaltung

Die nach der transformierten Gleichung aufgebaute Schaltung ist in Abb. dargestellt. 5,50.

Zwei von drei wechseln

Anlagen mit erhöhtem Risiko, wie zum Beispiel ein Kernkraftwerk, müssen im Falle eines Unfalls sofort abgeschaltet werden. Die Abschaltung erfolgt automatisch über eine digitale Schaltung. Bei Notsensoren, die für Abschaltungen verantwortlich sind, kann es zu Fehlalarmen kommen. Daher werden an jeder kritischen Stelle drei identische Notfallsensoren installiert (Abb. 5.51).
Die Abschaltung sollte nur erfolgen, wenn mindestens zwei der drei Alarmsensoren ausgelöst werden. Dieser Ansatz verhindert unnötige Systemabschaltungen, die zu finanziellen Verlusten führen. Bei Auslösung haben Notfallsensoren den Zustand 1. Das System sollte ausgeschaltet werden, wenn am Ausgang des Schaltkreises Zustand 1 aktiv ist.
Was also benötigt wird, ist eine Schaltung, deren Ausgang sich im Zustand 1 befindet, wenn mindestens zwei der drei Eingänge im Zustand 1 sind. Diese Schaltung wird als Zwei-von-Drei-Schalter bezeichnet.
Die Eingangsvariablen heißen A, B und C. Die Ausgangsvariable ist Z. Erstellen wir eine Wahrheitstabelle mit einer verbalen Beschreibung des Funktionsprinzips der Schaltung. Immer wenn zwei Eingangsvariablen gleich 1 sind, ist Z = 1. Wenn alle drei Eingangsvariablen gleich 1 sind, muss auch Z gleich 1 sein. Eine solche Wahrheitstabelle ist in Abb. dargestellt. 5.52.
Als nächstes wird gemäß der zusammengestellten Wahrheitstabelle die Normalform ODER geschrieben:

Reis. 5.51.

Z = (A a B a C) v (A a B a C) v a5aC|v(^aSaC).

Die Normalform von OR wird mithilfe eines Carnot-Diagramms vereinfacht (Abb. 5.53). Es können drei Doppelgruppen gebildet werden. Die vereinfachte Gleichung lautet:
Z = (AaB)w(BaC)w(AaC).
Mit dieser Gleichung können Sie ein Diagramm erstellen (Abb. 5.54).
Oft sind nur OR-HE-Elemente vorhanden. Um eine Schaltung aufzubauen, die nur OR-HE-Elemente verwendet, transformieren wir die Gleichung: in °-
Z = (AaB)v(BaC)v(AaC);
======= S O.
Z = (A l B)v (B aC)v (A lC);
—=====—= Abb. 5,55. Schaltkreis „zwei“
Z = AlVlVlSlAlS. von drei" auf Sh1I-NE-Elementen.
Das entsprechende Diagramm ist in Abb. dargestellt. 5,55.

Paritätsschaltung

Zur Erkennung von Fehlern in Codes (siehe Abschnitte 8.7 und 8.8) sowie für Steuerungs- und Überwachungsaufgaben wird häufig eine Schaltung benötigt, bei der der Ausgang 1 ist, wenn eine gerade Anzahl von Eingängen 1 ist.
Diese Schaltung wird Paritätsschaltung genannt.
Es ist erforderlich, eine Schaltung mit vier Eingängen zu synthetisieren. Die Eingabevariablen sind A, B, C und D. Die Ausgabevariable ist Y.
Zuerst müssen Sie eine Wahrheitstabelle erstellen. Y ist immer gleich 1, wenn 0, 2 oder 4 Eingangsvariablen gleich 1 sind (Abbildung 5.56).
Aus der Wahrheitstabelle erhalten wir die normale ODER-Form:
Y = (A l V lS l D)\/ ^A l V lS l (A l V lS l (A l V aS l
v(A l V lS l [A l V lS l (A l V lS l (A l V lS l D).

Einzelne vollständige Konjunktionen werden nummeriert. Versuchen wir, die Normalform von OR mithilfe einer Karnaugh-Karte zu vereinfachen (Abb. 5.57). Hier haben wir es mit dem seltenen Fall zu tun, dass die Bildung von Gruppen nicht möglich ist. Dies bedeutet, dass diese Normalform von OR nicht vereinfacht werden kann und ihr Diagramm in Abb. dargestellt ist. 5.58.

Eine Schwellenwertlogikschaltung ist eine Schaltung, bei der eine bestimmte Mindestanzahl von Eingangsvariablen den Zustand 1 haben muss, damit am Ausgang eine logische 1 erscheint.
Sie müssen beispielsweise eine Schaltung mit fünf Eingangsvariablen berechnen. Der Ausgang sollte nur dann 1 sein, wenn mindestens 4 Eingänge 1 sind.
Die Eingabevariablen heißen A, B, C, D und E. Die Ausgabevariable ist Z. Zuerst müssen wir die Wahrheitstabelle definieren. Bei fünf Variablen sind 32 Optionen möglich (Abb. 5.59):
Z =¦ (A l V lS l D l E^v (A l V lS l D l E)v (A l V lS l D l v^A l V lS l D l E^v [A l V lS l D l E^v (A l B lS l D l E).
Die Normalform OR besteht aus sechs vollständigen Konjunktionen.
Die Normalform von OR wird mithilfe eines Carnot-Diagramms vereinfacht (Abb. 5.60). Es können 5 Doppelgruppen gebildet werden. Daraus ergibt sich folgende vereinfachte logische Funktion:
Z = (A aBaCaE)v (A aBaDaE)v (A aBaCaD)v v(A aC a D a E)v (B aC a D a E).

Das Diagramm für die vereinfachte Funktion ist in Abb. dargestellt. 5.61. Diese Gleichung kann mithilfe der Algebra der Logik weiter vereinfacht werden. Für die ersten drei vollständigen Konjunktionen können wir aus Klammern (AaB) setzen, für die letzten beiden - (C l D). Die resultierende Funktion ist:
Z = [(A A B) A ((C A E) V (D A E) A C A X>))] V [(C A D) A ((A A E) V (B A Z))] . Eine nennenswerte Vereinfachung konnte jedoch nicht erreicht werden.

Vergleichsschaltung (Komparator)

In der digitalen Technologie müssen häufig digitale Daten miteinander verglichen werden. Die einfachste Vergleichsschaltung, der sogenannte Komparator, vergleicht den Zustand zweier Variablen miteinander.
Die Variablen seien mit A und B bezeichnet. A und B können gleich sein. A kann größer als B sein und umgekehrt. Der Komparator verfügt über drei Ausgänge für diese drei möglichen Optionen. Sie werden mit X, Y und Z bezeichnet und ihren Zuständen wie folgt zugeordnet:
A = Z => X = 1;
A > B^> Y= 1;
A< В =>Z = 1.
Es ist also notwendig, eine Schaltung mit zwei Eingangsvariablen A und B und Ausgangsvariablen X, Y und Z zu synthetisieren.
Beim Erstellen einer Wahrheitstabelle sollten Sie die Regeln beachten: A ist größer als B, wenn A = 1 und B = 0. Dementsprechend ist B größer als A, wenn B = 1 und A = 0. Die Wahrheitstabelle ist in Abb. dargestellt. 5.62.
Logische Funktionen werden aus der Wahrheitstabelle erhalten:
X = (AaB)v(AaB);
Y = A und B;
Z = A a B.
Diese Gleichungen werden nicht weiter vereinfacht. Das gewünschte Schema ist in Abb. dargestellt. 5.63.

Reis. 5.62.

Reis. 5.63.

Vor Verlassen des Werks werden Transistoren überprüft, um sicherzustellen, dass vier wichtige Parameter A, B, C und D im akzeptablen Bereich liegen. Zur Messung kommen vier digitale Sensoren zum Einsatz. Der Sensor gibt 1 aus, wenn der Messwert im zulässigen Bereich liegt. Liegt der Messwert außerhalb des akzeptablen Wertebereichs, gibt der Sensor 0 aus.
Transistoren werden mithilfe einer digitalen Schaltung sortiert. Wenn alle vier Werte innerhalb des akzeptablen Wertebereichs liegen, wird die Ausgabevariable M zu 1. Wenn nur B außerhalb des akzeptablen Wertebereichs liegt, wird die Ausgabevariable N zu 1. Wenn nur B und D außerhalb des akzeptablen Wertebereichs liegen Akzeptable Werte, dann erhält die Ausgangsvariable U den Zustand 1. In allen anderen Fällen ist der Ausgang Z 1, was bedeutet, dass der Transistor defekt ist.
Es ist erforderlich, die Schaltung zu berechnen und ausschließlich auf NAND-Elementen (auch „auf NAND-Basis“ genannt) aufzubauen.
Die Eingaben sind vier Variablen A, B, C und D. Die Ausgabevariablen sind M, N, U und Z. M wird 1, wenn A = 1, 5 = 1, C = 1 und D = 1. Dies ist Option 16 Zoll Wahrheitstabelle (Abb.
5.64). wird 1 sein, wenn A = \, 5 = 0, C = 1 und D = 1 (Option 14). U ist gleich 1, wenn A 1 ist, 5 = 0,
C = 1 und D = 0 (Option 6). In allen anderen Fällen, außer 6, 14 und 16, Z— 1.

Reis. 5,64. Wahrheitstabelle für Transistorsortierschaltung. Zur besseren Übersichtlichkeit werden Nullen für die Ausgangsvariable nicht geschrieben

Das Ergebnis sind die folgenden logischen Funktionen:
M = AaBaCaD;
N = A a B a C a D; U = A a B aC a D. Funktion Z enthält 13 vollständige Konjunktionen. Z ist dann immer 1, wenn weder M, N noch U gleich 1 sind. Besser ist es, die normale ODER-Form für Z zu schreiben (siehe Abb. 5.64):
Z = (^4a5aCaD)v^a5aCaD^v^aBaCaZ));
Z = M v N vU. Dann gilt für den direkten Wert von Z:
Z = M v N vU.

Reis. 5,65.

Die für M, Nn U gefundenen Funktionen können nicht vereinfacht werden. Sie müssen zusammen mit der Gleichung für Z auf die NAND-Basis umgerechnet werden:
M = AaBaCaD\
N = A a B aC l D;
U = AlVlSlO",
Z = M v N v U = M a N aU;
Z = M a N a U.
Aus diesen Gleichungen ergibt sich das in Abb. dargestellte Diagramm. 5,65. Über die Ausgänge M, N, U und Z kann ein mechanisches Gerät gesteuert werden, das die Transistoren auf 4 verschiedene Behälter verteilt.

Bei der Implementierung analoger Signalverarbeitungsalgorithmen ist es häufig erforderlich, mathematische Funktionen zu berechnen. Die gebräuchlichsten Funktionen sind Logarithmus- und Exponentialfunktionen. Diese Funktionen werden in Schemata verwendet, um den Dynamikbereich eines übertragenen oder aufgezeichneten Signals zu reduzieren und zu erhöhen (Kompansion). Eine weitere häufige Anwendung von Exponenten- und Logarithmus-Matheschaltungen ist die Berechnung des Produkts und der Division von Eingangssignalen.

Um eine nichtlineare Funktion zu berechnen, wird häufig ein Operationsverstärker mit negativer Rückkopplung verwendet. Als Beispiel zeigt Abbildung 1 die Schaltung eines logarithmischen Verstärkers.

Abbildung 1. Logarithmische Verstärkerschaltung

In dieser Schaltung ist ein nichtlineares Element (Halbleiterdiode) im Gegenkopplungskreis enthalten, das eine exponentielle Abhängigkeit des Stroms von der angelegten Spannung aufweist. Durch die Rückkopplung wird die Abhängigkeit der Ausgangsspannung vom Eingang logarithmisch. Die Verstärkung dieser Logarithmusschaltung wird durch R1 bestimmt. Typischerweise ist die Logarithmusschaltung auf eine Verstärkung von eins ausgelegt.

Wird in dieser Schaltung eine Diode mit quadratischer Strom-Spannungs-Kennlinie verwendet, so berechnet diese die Quadratwurzel des Eingangssignals. Es lässt sich bequem in Schaltkreisen zur Bestimmung der Signalamplitude während der Quadratursignalverarbeitung verwenden.

(1),

Die Umkehrung der logarithmischen Funktion, die Exponentialfunktion, wird auf ähnliche Weise berechnet. Nur in diesem Fall ist das nichtlineare Element nicht im Rückkopplungskreis enthalten, sondern am Eingang des Verstärkers. Abbildung 2 zeigt ein Diagramm zur Berechnung des Exponenten an einem Operationsverstärker.

Abbildung 2. Schema zur Berechnung des Exponenten

Wird in dieser Schaltung eine Diode mit quadratischer Strom-Spannungs-Kennlinie verwendet, berechnet die Schaltung das Quadrat der Eingangsspannung und kann als Schaltung zur Bestimmung der Eingangssignalleistung verwendet werden.

Mit diesen Schaltkreisen zur Berechnung mathematischer Funktionen können Sie das Produkt zweier analoger Signale berechnen. Dabei wird die bekannte Eigenschaft von Logarithmen genutzt, um das Produkt von Variablen durch die Summe der Logarithmen dieser Variablen zu ersetzen. Für die inverse Konvertierung wird die Exponentenberechnungsfunktion verwendet. In diesem Fall ist die Basis des Logarithmus völlig unwichtig.

(2),

Die Multiplizierschaltung, die Formel (1) auf Operationsverstärkern umsetzt, ist in Abbildung 3 dargestellt.

Abbildung 3. Operationsverstärker-Multipliziererschaltung

Trotz der Einfachheit der Implementierung wird ein solches Schema recht selten verwendet, weil Eine Multiplikation ist nur für positive Eingabewerte möglich. Daher werden üblicherweise auf dieser Basis aufgebaute Multiplizierschaltungen verwendet.

Zur Berechnung von Funktionen ist es nicht immer möglich, ein nichtlineares Element mit einer bestimmten Strom-Spannungs-Kennlinie auszuwählen. In diesem Fall können Sie eine stückweise lineare Approximation der Funktion verwenden. Es ist einfach, eine beliebige Verstärkung an einem Operationsverstärker zu implementieren, indem man einfach den Wert des Widerstands im Rückkopplungskreis ändert und so die Steigung der Funktion festlegt. Das Schalten von Widerständen bei Änderung der Eingangsspannung gelingt am einfachsten mit Diodenschaltern, die mit der von uns eingestellten Abschaltspannung versorgt werden. Ein ähnliches Diagramm ist in Abbildung 4 dargestellt.

Abbildung 4. Funktionsverstärkerschaltung

Transistorbasierte Multiplikatoren werden häufig zur Berechnung komplexerer Funktionen verwendet. Im einfachsten Fall können die X- und Y-Eingänge kombiniert werden, um eine Schaltung zur Berechnung des Quadrats des Eingangssignals zu erhalten ( Y=X 2).

Sie können als elektronische Spannungsregler eingesetzt werden. Durch Anlegen einer konstanten Spannung an einen der Eingänge können Sie am Ausgang die Höhe der dem Ausgang zugeführten Wechselspannung regulieren.

Literatur:

Zusammen mit dem Artikel „Schemata zur Berechnung mathematischer Funktionen“ lesen Sie:

2.1 Entwicklung des Algorithmus.

Algorithmus- Das

A. Beschreibung der Abfolge von Maßnahmen zur Lösung eines Problems oder zur Erreichung eines Ziels;

B. Regeln für die Durchführung grundlegender Datenverarbeitungsvorgänge;

C. Beschreibung von Berechnungen mit mathematischen Formeln.

Bevor mit der Entwicklung eines Algorithmus begonnen wird, ist es notwendig, die Aufgabe klar zu verstehen: Was muss als Ergebnis erhalten werden, welche Ausgangsdaten werden benötigt und was ist verfügbar, welche Einschränkungen bestehen für diese Daten. Als nächstes müssen Sie aufschreiben, welche Maßnahmen ergriffen werden müssen, um aus den Ausgangsdaten das gewünschte Ergebnis zu erhalten.

In der Praxis sind die häufigsten Formen der Darstellung von Algorithmen:

Verbal (Aufzeichnungen in natürlicher Sprache);

Grafik (Bilder aus grafischen Symbolen);

Pseudocodes (halbformalisierte Beschreibungen von Algorithmen in einer bedingten algorithmischen Sprache, einschließlich sowohl Elementen einer Programmiersprache als auch natürlichsprachlicher Phrasen, allgemein akzeptierter mathematischer Notationen usw.);

Software (Texte in Programmiersprachen).

Die verbale Schreibweise von Algorithmen ist eine Beschreibung der aufeinanderfolgenden Phasen der Datenverarbeitung. Der Algorithmus wird in freier Form in natürlicher Sprache spezifiziert.

Beispiel. Schreiben Sie einen Algorithmus zum Ermitteln des größten gemeinsamen Teilers (GCD) zweier natürlicher Zahlen auf.

Der Algorithmus könnte wie folgt aussehen:

1. zwei Zahlen einstellen;

2. Wenn die Zahlen gleich sind, nehmen Sie eine davon als Antwort und stoppen Sie, andernfalls fahren Sie mit der Ausführung des Algorithmus fort;

3. Bestimmen Sie die größte der Zahlen;

4. Ersetzen Sie die größere Zahl durch die Differenz zwischen der größeren und der kleineren Zahl.

5. Wiederholen Sie den Algorithmus ab Schritt 2.

Der beschriebene Algorithmus ist auf beliebige natürliche Zahlen anwendbar und soll zu einer Lösung des Problems führen. Überzeugen Sie sich selbst, indem Sie mit diesem Algorithmus den größten gemeinsamen Teiler der Zahlen 125 und 75 ermitteln.

Die verbale Methode ist aus folgenden Gründen nicht weit verbreitet:

Solche Beschreibungen sind nicht streng formalisierbar;

Leiden Sie unter der Worthaftigkeit der Notizen;

Bei der Auslegung einzelner Regelungen bestehen Unklarheiten.

Die grafische Darstellung von Algorithmen ist im Vergleich zur verbalen Darstellung kompakter und visueller.

Bei der grafischen Darstellung wird der Algorithmus als eine Folge miteinander verbundener Funktionsblöcke dargestellt, von denen jeder der Ausführung einer oder mehrerer Aktionen entspricht.

Diese grafische Darstellung wird Flussdiagramm oder Flussdiagramm genannt.

Pseudocode ist ein System von Notationen und Regeln zum einheitlichen Schreiben von Algorithmen.

Es nimmt eine Zwischenstellung zwischen natürlichen und formalen Sprachen ein.

Einerseits ähnelt es der gewöhnlichen natürlichen Sprache, sodass Algorithmen wie normaler Text darin geschrieben und gelesen werden können. Andererseits verwendet Pseudocode einige formale Konstrukte und mathematische Symbolik, was die Algorithmusnotation näher an die allgemein akzeptierte mathematische Notation bringt.

Im Pseudocode werden keine strengen syntaktischen Regeln zum Schreiben von Befehlen übernommen, die formalen Sprachen innewohnen, was das Schreiben des Algorithmus in der Entwurfsphase erleichtert und die Verwendung eines größeren Satzes von Befehlen ermöglicht, die für einen abstrakten Ausführenden konzipiert sind. Pseudocode enthält jedoch normalerweise einige Konstrukte, die formalen Sprachen innewohnen, was den Übergang vom Schreiben in Pseudocode zum Schreiben eines Algorithmus in einer formalen Sprache erleichtert. Insbesondere im Pseudocode sowie in formalen Sprachen gibt es Funktionswörter, deren Bedeutung ein für alle Mal festgelegt ist. Es gibt keine einheitliche oder formale Definition von Pseudocode, daher sind verschiedene Pseudocodes möglich, die sich in der Menge der Funktionswörter und grundlegenden (Grund-)Konstruktionen unterscheiden.

2.2 Blockdiagramm.

Ein Flussdiagramm ist eine grafische Darstellung eines Algorithmus, in der dieser als Folge miteinander verbundener Funktionsblöcke dargestellt wird, von denen jeder der Ausführung einer oder mehrerer Aktionen entspricht.

Im Flussdiagramm entspricht jede Art von Aktion (Eingabe von Anfangsdaten, Berechnung der Werte von Ausdrücken, Überprüfung von Bedingungen, Steuerung der Wiederholung von Aktionen, Abschluss der Verarbeitung usw.) einer geometrischen Figur, die als Blocksymbol dargestellt wird. Blocksymbole sind durch Übergangslinien verbunden, die die Reihenfolge bestimmen, in der Aktionen ausgeführt werden.

Hier sind die am häufigsten verwendeten Symbole.

Symbolname	Bezeichnung und Füllbeispiel	Erläuterung
Verfahren		Rechenaktion oder Folge von Aktionen
Lösung		Bedingungen prüfen
Änderung		Beginn des Zyklus
Vordefinierter Prozess		Berechnungen nach Unterprogramm, Standard-Unterprogramm
Input-Output		E/A im Allgemeinen
Start stop		Anfang, Ende des Algorithmus, Ein- und Ausstieg in das Unterprogramm
Dokumentieren		Druckergebnisse

Der Block „Prozess“ wird verwendet, um eine Aktion oder eine Folge von Aktionen zu bezeichnen, die die Bedeutung, Form der Darstellung oder Platzierung von Daten ändert. Um die Übersichtlichkeit des Diagramms zu verbessern, können mehrere einzelne Verarbeitungsblöcke zu einem Block zusammengefasst werden. Die Darstellung einzelner Operationen ist völlig kostenlos.

Der Block „Entscheidung“ wird verwendet, um bedingte Steuerübergänge anzuzeigen. Jeder „Lösungs“-Block muss die Frage, Bedingung oder den Vergleich identifizieren, die er definiert.

Der Block „Modifikation“ dient der Organisation zyklischer Strukturen. (Das Wort Modifikation bedeutet Modifikation, Transformation). Innerhalb des Blocks wird ein Zyklusparameter geschrieben, dessen Anfangswert, Randbedingung und Schritt der Änderung des Parameterwerts für jede Wiederholung angegeben werden.

Der Block „vordefinierter Prozess“ wird verwendet, um Aufrufe von Hilfsalgorithmen anzuzeigen, die autonom in Form einiger unabhängiger Module existieren, sowie für Aufrufe von Bibliotheksroutinen.

Beispiel. Erstellen Sie ein Blockdiagramm eines Algorithmus zur Bestimmung der Höhen ha, hb, hc eines Dreiecks mit den Seiten a, b, c, if

Wo p = (a + b + c) / 2.
Lösung. Lassen Sie uns die Notation einführen dann h a = t/a, h b = t/b, h c = t/c. Das Flussdiagramm muss Start, Eingabe a, b, c, Berechnung p, t, h enthalten a, h b, h c , Ergebnisse ausgeben und stoppen.

2.3 Algorithmusstrukturen.

Algorithmen kann man sich als bestimmte Strukturen vorstellen, die aus einzelnen Grundelementen bestehen. Natürlich sollte bei dieser Herangehensweise an Algorithmen das Studium der Grundprinzipien ihres Designs mit dem Studium dieser Grundelemente beginnen

Die logische Struktur eines jeden Algorithmus kann durch eine Kombination aus drei Grundstrukturen dargestellt werden: Folgen, Verzweigen und Schleifen.

Ein charakteristisches Merkmal grundlegender Strukturen ist das Vorhandensein eines Eingangs und eines Ausgangs.

1. Es folgt die Grundstruktur. Gebildet aus einer Abfolge aufeinanderfolgender Aktionen:

2. Grundlegende Verzweigungsstruktur. Bietet abhängig vom Ergebnis der Überprüfung der Bedingung (Ja oder Nein) die Wahl einer der alternativen Betriebsweisen des Algorithmus. Jeder Pfad führt zu einem gemeinsamen Ausgang, sodass der Algorithmus unabhängig vom gewählten Pfad weiter ausgeführt wird.

Struktur Verzweigung existiert in vier Hauptvarianten:

Wenn-dann-sonst;

Die Wahl ist anders.

1) Wenn-Wenn-Bedingung, dann Aktion beenden, wenn 2) if-else if Bedingung dann Aktionen 1 sonst Aktionen 2 Ende wenn 3) Auswahlauswahl mit Bedingung 1: Aktionen 1 mit Bedingung 2: Aktionen 2. . . . . . . . . . . . unter Bedingung N: Aktionen N Ende der Wahl 4) Wahl – ansonsten Wahl unter Bedingung 1: Aktion 1 unter Bedingung 2: Aktion 2. . . . . . . . . . . . unter Bedingung N: Aktionen N, sonst Aktionen N+1 Ende der Wahl

Beispiel. Erstellen Sie ein Blockdiagramm des Algorithmus zur Berechnung der Funktion

Die Grundstruktur ist ein Kreislauf. Ermöglicht die wiederholte Ausführung einer bestimmten Reihe von Aktionen, die als Schleifenkörper bezeichnet werden.

Die Zyklusstruktur besteht in drei Hauptversionen:

Schleifentyp Für.

Weist an, den Schleifenkörper für alle Werte einer bestimmten Variablen (Schleifenparameter) in einem bestimmten Bereich auszuführen.

Schleifentyp Tschüss.

Befiehlt die Ausführung des Schleifenkörpers, solange die nach dem Wort while geschriebene Bedingung erfüllt ist.

Schleifentyp tun während.

Befiehlt die Ausführung des Schleifenkörpers, solange die nach dem Wort while geschriebene Bedingung erfüllt ist. Die Bedingung wird überprüft, nachdem der Schleifenkörper ausgeführt wurde.

Beachten Sie, dass for- und while-Schleifen auch als Schleifen mit Vorabprüfung der Bedingung bezeichnet werden und Schleifen to do – while – Schleifen mit Nachprüfung der Bedingung. Mit anderen Worten: Die Körper der for- und while-Schleifen werden möglicherweise nicht einmal ausgeführt, wenn die Endbedingung der Schleife anfänglich nicht wahr ist. Führen Sie den Schleifenkörper aus, bis er mindestens einmal ausgeführt wird, auch wenn die Bedingung zum Beenden der Schleife zunächst nicht wahr ist.

Zyklus für i von i1 bis i2 Schritt i3 Zykluskörper (Abfolge von Aktionen) Ende des Zyklus Schleife während Bedingung Schleifenkörper (Abfolge von Aktionen) Ende der Schleife Durchlaufen Sie den Schleifenkörper (Abfolge von Aktionen) bis zum Ende der Schleife

mit einer gegebenen Genauigkeit (für eine gegebene Wechselleistungsreihe wird die erforderliche Genauigkeit erreicht, wenn der nächste Term im Absolutwert kleiner wird).

Das Berechnen von Summen ist eine typische zyklische Aufgabe. Die Besonderheit unseres spezifischen Problems besteht darin, dass die Anzahl der Terme (und damit die Anzahl der Wiederholungen des Schleifenkörpers) im Voraus unbekannt ist. Daher muss die Schleife beendet werden, wenn die erforderliche Genauigkeit erreicht ist.

Beim Kompilieren eines Algorithmus müssen Sie berücksichtigen, dass sich die Vorzeichen der Terme abwechseln und die Potenz der Zahl x in den Zählern der Terme zunimmt.

Lösen Sie dieses Problem direkt, indem Sie die Teilsumme bei jedem i-ten Schritt berechnen

S:=S+(-1)**(i-1)*x**i/i ,

Am Ende erhalten wir einen sehr ineffizienten Algorithmus, der eine große Anzahl von Operationen erfordert. Es ist viel besser, die Berechnungen wie folgt zu organisieren: Wenn Sie den Zähler eines beliebigen Termes mit dem Buchstaben p bezeichnen, dann ist der Zähler des nächsten Termes gleich -р*х (das Minuszeichen sorgt für den Vorzeichenwechsel von). die Terme), und der Term selbst wird m sein

wird gleich p/i sein, wobei i die Zahl des Termes ist.

Ein Algorithmus, der eine iterative Schleife enthält, wird als iterativer Algorithmus bezeichnet. Iterative Algorithmen werden bei der Implementierung iterativer numerischer Verfahren verwendet. Bei iterativen Algorithmen muss sichergestellt werden, dass die Bedingung zum Verlassen des Zyklus erfüllt ist (Konvergenz des iterativen Prozesses). Andernfalls führt der Algorithmus eine Schleife aus, d. h. die Haupteigenschaft des Algorithmus – die Wirksamkeit – wird nicht erfüllt.

Verschachtelte Schleifen.

Es kann Fälle geben, in denen es notwendig ist, eine bestimmte Folge von Anweisungen innerhalb des Schleifenkörpers zu wiederholen, also eine innere Schleife zu organisieren. Diese Struktur wird als Schleife innerhalb einer Schleife oder als verschachtelte Schleifen bezeichnet. Die Verschachtelungstiefe von Schleifen (also die Anzahl der ineinander verschachtelten Schleifen) kann unterschiedlich sein.

Um Computerzeit zu sparen, ist es bei Verwendung einer solchen Struktur erforderlich, alle Anweisungen, die nicht vom Parameter der inneren Schleife abhängen, von der inneren Schleife in die äußere zu verschieben.

Beispiel verschachtelte Schleifen für. Berechnen Sie die Summe der Elemente der gegebenen Matrix A(5,3).

Beispiel verschachtelte Schleifen vorerst. Berechnen Sie das Produkt der Elemente der gegebenen Matrix A(10,10), die sich am Schnittpunkt gerader Zeilen und gerader Spalten befinden.