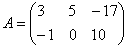Πώς να υπολογίσετε το προϊόν των πινάκων. Δράσεις μήτρας

Έτσι, στο προηγούμενο μάθημα, συζητήσαμε τους κανόνες προσθήκης και αφαίρεσης των πινάκων. Αυτές οι λειτουργίες είναι τόσο απλές που οι περισσότεροι μαθητές τις παίρνουν κυριολεκτικά εν κινήσει.

Ωστόσο, χαίρεσαι νωρίς. Freebie over - πηγαίνετε στον πολλαπλασιασμό. Αμέσως θα σας προειδοποιήσω: να πολλαπλασιάσετε δύο μήτρες δεν είναι να πολλαπλασιάσετε τους αριθμούς στα κελιά με τις ίδιες συντεταγμένες, όπως θα σκεφτόσαστε. Είναι πολύ πιο διασκεδαστικό. Και πρέπει να ξεκινήσετε με προκαταρκτικούς ορισμούς.

Αντιστοιχισμένες μήτρες

Ένα από τα πιο σημαντικά χαρακτηριστικά της μήτρας είναι το μέγεθός της. Έχουμε ήδη μιλήσει για αυτό εκατό φορές: γράφοντας $ A = \\ left [m \\ times n \\ right] $ σημαίνει ότι υπάρχουν ακριβώς στήλες $ m $ rows και $ n $ στη μήτρα. Πώς να μην συγχέουμε σειρές με στήλες, συζητήσαμε επίσης. Τώρα το άλλο είναι σημαντικό.

Ορισμός Οι μήτρες της φόρμας $ A = \\ left [m \\ times n \\ right] $ και $ B = \\ left [n \\ times k \\ right] $, όπου ο αριθμός των στηλών στην πρώτη μήτρα συμπίπτει με τον αριθμό των γραμμών στο δεύτερο.

Για άλλη μια φορά: ο αριθμός των στηλών στην πρώτη μήτρα είναι ίσος με τον αριθμό των γραμμών στο δεύτερο! Από εδώ έχουμε δύο συμπεράσματα:

1. Η σειρά των πινάκων είναι σημαντική για εμάς. Για παράδειγμα, οι πίνακες $ A = \\ left [3 \\ times 2 \\ right] $ και $ B = \\ left [2 \\ times 5 \\ right] $ είναι συνεπείς (2 στήλες στην πρώτη μήτρα και 2 σειρές στο δεύτερο) - οι πίνακες $ B = \\ left [2 \\ times 5 \\ right] $ και $ A = \\ left [3 \\ times 2 \\ right] $ δεν ταιριάζουν πλέον (5 στήλες στην πρώτη μήτρα δεν είναι 3 σειρές στο δεύτερο ).
2. Η συνέπεια είναι εύκολο να ελέγξετε αν γράφετε όλα τα μεγέθη το ένα μετά το άλλο. Στο παράδειγμα από την προηγούμενη παράγραφο: "3 2 2 5" - οι ίδιοι αριθμοί στη μέση, συνεπώς οι πίνακες είναι συνεπείς. Αλλά το "2 5 3 2" δεν είναι συντονισμένο, δεδομένου ότι υπάρχουν διάφοροι αριθμοί στη μέση.

Επιπλέον, ο καπετάνιος υποδεικνύει προφανώς ότι οι τετράγωνες μήτρες του ίδιου μεγέθους $ \\ left [n \\ times n \\ right] $ είναι πάντα συνεπείς.

Στα μαθηματικά, όταν η σειρά απαρίθμησης αντικειμένων είναι σημαντική (για παράδειγμα, στον παραπάνω ορισμό, η σειρά των πινάκων είναι σημαντική), λέγεται συχνά για τα ταξινομημένα ζεύγη. Συναντηθήκαμε μαζί τους στο σχολείο: Νομίζω ότι, και μια μη-brainer ότι οι συντεταγμένες $ \\ left (1; 0 \\ right) $ και $ \\ left (0; 1 \\ right) $ ορίζουν διαφορετικά σημεία στο αεροπλάνο.

Έτσι: οι συντεταγμένες ταξινομούνται επίσης ζεύγη, τα οποία αποτελούνται από αριθμούς. Αλλά τίποτα δεν εμποδίζει να δημιουργήσει ένα τέτοιο ζευγάρι πινάκων. Στη συνέχεια μπορούμε να πούμε: "Ένα ταξινομημένο ζεύγος πινάκων $ \\ left (A; B \\ right) $ είναι συνεπές αν ο αριθμός των στηλών στην πρώτη μήτρα συμπίπτει με τον αριθμό των γραμμών στο δεύτερο."

Λοιπόν, λοιπόν;

Ορισμός πολλαπλασιασμού

Εξετάστε δύο συνεχείς μήτρες: $ A = \\ left [m \\ times n \\ right] $ και $ B = \\ left [n \\ times k \\ right] $. Και καθορίζουμε γι 'αυτούς τη λειτουργία πολλαπλασιασμού.

Ορισμός Το προϊόν των δύο συμβατών πινάκων $ A = \\ left [m \\ times n \\ right] $ και $ B = \\ left [n \\ times k \\ right] $ είναι ο νέος πίνακας $ C = \\ left [m \\ times k \\ $, τα στοιχεία των οποίων υπολογίζονται από τον τύπο:

\\ (1)) + ((a)) () () () (2)) \\ cdot ((b) _ (2; j)) + \\ ldots + (a) _ (i; n)) \\ cdot Ένα τέτοιο προϊόν συμβολίζεται ως πρότυπο: $ C = A \\ cdot B $.

Για όσους βλέπουν αυτόν τον ορισμό για πρώτη φορά, προκύπτουν αμέσως δύο ερωτήματα:

Τι είναι αυτό το άγριο παιχνίδι;

1. Γιατί τόσο σκληρά;
2. Λοιπόν, πρώτα πρώτα. Ας ξεκινήσουμε με την πρώτη ερώτηση. Τι σημαίνουν όλοι αυτοί οι δείκτες; Και πώς να μην συγχέεται όταν εργάζεστε με πραγματικές μήτρες;

Πρώτα απ 'όλα, σημειώνουμε ότι η μακρά γραμμή για τον υπολογισμό του $ ((c) _ (i; j)) $ (τοποθετήστε συγκεκριμένα ένα ερωτηματικό μεταξύ των δεικτών για να μην συγχέεται, αλλά γενικά δεν πρέπει να τεθούν - έχω πληρώσει τον τύπο στον ορισμό) στην πραγματικότητα καταλήγει σε έναν απλό κανόνα:

Πάρτε τη $ i $ th γραμμή στην πρώτη μήτρα.

1. Πάρτε τη στήλη $ j $ th στη δεύτερη μήτρα.
2. Παίρνουμε δύο ακολουθίες αριθμών. Πολλαπλασιάστε τα στοιχεία αυτών των ακολουθιών με τους ίδιους αριθμούς και, στη συνέχεια, προσθέστε τις εργασίες που προκύπτουν.
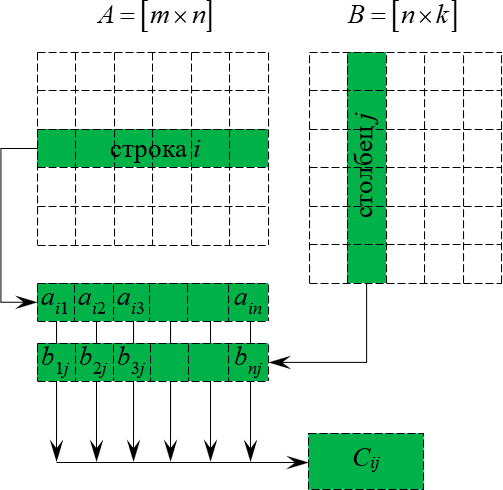
3. Αυτή η διαδικασία είναι εύκολο να κατανοηθεί από την εικόνα:

   Σχέδιο πολλαπλασιασμού δύο μητρών

Για άλλη μια φορά: διορθώστε τη σειρά $ i $ στον πρώτο πίνακα, τη στήλη $ j $ στη δεύτερη μήτρα, πολλαπλασιάστε τα στοιχεία με τους ίδιους αριθμούς και στη συνέχεια προσθέστε τα προκύπτοντα προϊόντα - παίρνουμε $ ((c) _ (ij)) $. Και για όλα τα $ 1 \\ le i \\ le m $ και $ 1 \\ le j \\ le k $. Δηλαδή συνολικά θα υπάρχουν $ m \\ φορές k $ τέτοιων "διαστροφών".

Στην πραγματικότητα, έχουμε ήδη συναντήσει τον πολλαπλασιασμό των πινάκων στο σχολικό πρόγραμμα σπουδών, μόνο σε μια πολύ κολοσσιαία μορφή. Αφήστε τα διανύσματα να δοθούν:

\\ (\\ (\\) \\ (\\ a \\) \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\\\ & \\ overrightarrow (b) = \\ αριστερά (((x) _ (b)), (y) _ (b)), (z) _b)) δεξιά. \\\\ \\ end (ευθυγράμμιση) \\]

Τότε το βαθμωτό προϊόν τους θα είναι ακριβώς το άθροισμα των ζευγαριών προϊόντων:

{!LANG-29cb3b97ac1718c2e1e857e7325cce66!}

\\ (\\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ (\\) \\ ) β)) + ((z) _ (a)) \\ cdot ((z) _ (b)) \\

Στην πραγματικότητα, σε αυτά τα μακρινά χρόνια, όταν τα δέντρα ήταν πιο πράσινα και ο ουρανός φωτεινότερα, απλά πολλαπλασιάσαμε τον διάνυσμα γραμμών $ \\ overrightarrow (a) $ από το διάνυσμα στήλης $ \\ overrightarrow (b) $.

Σήμερα, τίποτα δεν άλλαξε. Ακριβώς τώρα αυτοί οι διανύσματα σειράς και στήλες έγιναν περισσότερο.

Αλλά αρκετά από τη θεωρία! Ας δούμε πραγματικά παραδείγματα. Και ας ξεκινήσουμε με την απλούστερη περίπτωση - τετράγωνες μήτρες.

Πολλαπλασιασμός τετραγωνικών πινάκων

Εργασία 1. Εκτέλεση πολλαπλασιασμού:

\\ [\\ left \\ \\ start (array) (* (35) (r)) 1 & 2 \\\\ 3 & 4 \\\\\\ τέλος (array) (35) (r)) -2 & 4 \\\\ 3 & 1 \\\\\\ τέλος (πίνακας) \\ δικαίωμα] \\]

Η απόφαση. Έτσι, έχουμε δύο μήτρες: $ A = \\ αριστερά [2 \\ φορές 2 \\ δεξιά] $ και $ B = \\ αριστερά [2 \\ φορές 2 \\ δεξιά] $. Είναι σαφές ότι είναι συνεπείς (οι τετράγωνες μήτρες του ίδιου μεγέθους είναι πάντα συνεπείς). Επομένως, εκτελούμε τον πολλαπλασιασμό:

\\ [\\ begin \\ (\\ align) \\ \\ left \\ \\ begin (array) (* (35) 1 \\ cdot \\ αριστερά (-2 \\ δεξιά) + 2 \\ cdot 3 & 1 \\ cdot 4 + 2 \\ cdot 1 \\\\ -3 \\ cdot \\ 4 + 4 \\ cdot 1 \\\\\\ τέλος (array) \\ right] = \\\\ & = \\ left [\\ begin (array) \\ end (ευθυγράμμιση) \\]

Αυτό είναι!

Απάντηση: $ \\ left [\\ begin (array)] (* (35) (r)) 4 & 6 \\\\ 18 & 8 \\\\\\ τέλος (array) \\ right] $.

Εργασία 2. Εκτέλεση πολλαπλασιασμού:

\\ [\\ left \\ \\ begin (matrix) 1 & 3 \\\\ 2 & 6 \\\\\\ τέλος (μήτρα) \\ δεξιά] \\ cdot \\ left [\\ begin (array) \\\\ -3 & -2 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Η απόφαση. Πάλι αντιστοιχισμένες μήτρες, ώστε να εκτελέσουμε τις ενέργειες: \\ [\\]

\\ [\\ begin (matrix) 1 & 3 \\\\ 2 & 6 \\\\\\ end (matrix) \\ right] \\ cdot \\ left [\\ begin (array) r)) 9 & 6 \\\\ 3 & -2 \\\\\\ τέλος (array) \\ right] = \\ αριστερά [\\ begin (array)] * \\ cdot 9 + 3 \\ cdot \\ cdot \\ left (-2 \\ right) \\\\\\ end (array) \\ right] = \\\\ & = \\ left [\\ matrix] 0 & 0 \\\\ 0 & 0 \\\\\\ end (matrix) . \\ end (ευθυγράμμιση) \\]

Όπως μπορείτε να δείτε, το αποτέλεσμα είναι μια μήτρα γεμάτη με μηδενικά.

Απάντηση: $ \\ left [\\ begin (matrix) 0 & 0 \\\\ 0 & 0 \\\\\\ τέλος (μήτρα) \\ δεξιά] $.

Από τα παραδείγματα που δίνονται είναι προφανές ότι ο πολλαπλασιασμός των πινάκων δεν είναι τόσο περίπλοκη λειτουργία. Τουλάχιστον για τετραγωνικές μήτρες μεγέθους 2 έως 2.

Κατά τη διάρκεια των υπολογισμών, έχουμε συντάξει μια ενδιάμεση μήτρα, όπου έχουμε περιγράψει άμεσα ποιοι αριθμοί ανήκουν σε ένα ή άλλο κελί. Αυτό ακριβώς πρέπει να γίνει κατά την επίλυση πραγματικών προβλημάτων.

Οι κύριες ιδιότητες του προϊόντος μήτρας

Με λίγα λόγια. Πολλαπλασιασμός μήτρας:

1. Μη μετακινούμενο: $ A \\ cdot B \\ ne B \\ cdot A $ στη γενική περίπτωση. Υπάρχουν, βεβαίως, ειδικοί πίνακες για τους οποίους η ισότητα $ A \\ cdot B = B \\ cdot A $ (για παράδειγμα, εάν $ B = E $ είναι ο πίνακας ταυτότητας), αλλά στις περισσότερες περιπτώσεις αυτό δεν λειτουργεί.
2. Συνεργατικά: $ \\ αριστερά (A \\ cdot B \\ δεξιά) \\ cdot C = A \\ cdot \\ αριστερά (B \\ cdot C \\ δεξιά) $. Δεν υπάρχουν επιλογές εδώ: μπορείτε να πολλαπλασιάσετε τις μήτρες που βρίσκονται κοντά, χωρίς να ανησυχείτε για το τι έχει απομείνει και δεξιά από αυτές τις δύο μήτρες.
3. Διανεμητικά: $ A \\ cdot \\ αριστερά (B + C \\ δεξιά) = A \\ cdot B + A \\ cdot C $ και $ \\ αριστερά (A + B \\ right) \\ cdot C = A \\ cdot C + B \\ cdot C $ (εξαιτίας της μη εναλλαξιμότητας του προϊόντος, είναι απαραίτητο να συνταγογραφηθεί η διανομή χωριστά στα δεξιά και στα αριστερά.

Και τώρα - όλα αυτά, αλλά με περισσότερες λεπτομέρειες.

Ο πολλαπλασιασμός των πινάκων θυμίζει με πολλούς τρόπους τον κλασικό πολλαπλασιασμό των αριθμών. Αλλά υπάρχουν διαφορές, το πιο σημαντικό από τα οποία είναι αυτό ο πολλαπλασιασμός της μήτρας, γενικά, δεν είναι μεταλλαξιογόνος.

Ας εξετάσουμε και πάλι τις μήτρες από το πρόβλημα 1. Γνωρίζουμε ήδη το άμεσο προϊόν τους:

\\ [\\ left \\ \\ start (array) (* (35) (r)) 1 & 2 \\\\ 3 & 4 \\\\\\ τέλος (array) (35) (r)) -2 & 4 \\\\ 3 & 1 \\\\ τέλος (array) \\ right] = \\ left [\\ begin (array) & -8 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Αλλά αν αλλάζετε μήτρες σε μέρη, παίρνετε ένα εντελώς διαφορετικό αποτέλεσμα:

\\ \\ \\ left \\ \\ start (array) (* (35) (r)) -2 & 4 \\\\ 3 & 1 \\\\\\ τέλος (array) \\ right] \\ cdot \\ (35) (r)) 1 & 2 \\\\ 3 & 4 \\\\ τέλος (πίνακας) \\ δεξιά] = \\ αριστερά [\\ matrix] -14 & 4 \\\\ 0 & ) \\ δεξιά] \\]

Αποδεικνύεται ότι το $ A \\ cdot B \\ ne B \\ cdot A $. Επιπλέον, η λειτουργία πολλαπλασιασμού ορίζεται μόνο για τους πίνακες $ a = \\ left [m \\ times n \\ right] $ και $ B = \\ left [n \\ times k \\ right] $, αλλά κανείς δεν εγγυάται ότι θα παραμείνουν συνεπείς, αν τα ανταλλάξετε. Για παράδειγμα, οι πίνακες $ \\ left [2 \\ times 3 \\ right] $ and $ \\ left [3 \\ times 5 \\ right] $ είναι αρκετά συνεπείς με την καθορισμένη σειρά, αλλά οι ίδιες πίνακες $ \\ left [3 \\ times 5 \\ right] Οι $ και $ \\ left [2 \\ times 3 \\ right] $, γραμμένες με αντίστροφη σειρά, δεν είναι πλέον συνεπείς. Θλίψη. :(

Μεταξύ των τετραγωνικών πινάκων ενός δεδομένου μεγέθους $ n $, υπάρχουν πάντα εκείνοι που δίνουν το ίδιο αποτέλεσμα τόσο όταν πολλαπλασιάζονται σε άμεση όσο και σε αντίστροφη σειρά. Πώς να περιγράψουμε όλες αυτές τις μήτρες (και πόσοι είναι εκεί καθόλου) είναι ένα θέμα για ένα ξεχωριστό μάθημα. Σήμερα δεν θα μιλήσουμε γι 'αυτό. :)

Ωστόσο, ο πολλαπλασιασμός της μήτρας είναι συσχετιστικός:

\\ \\ \\ αριστερά (A \\ cdot B \\ δεξιά) \\ cdot C = A \\ cdot \\ αριστερά (B \\ cdot C \\

Επομένως, όταν χρειάζεται να πολλαπλασιάσετε πολλές μήτρες σε μια σειρά ταυτόχρονα, δεν είναι απαραίτητο να το κάνετε σωστά μέσω: είναι πιθανό μερικές γειτονικές μήτρες να δίνουν ένα ενδιαφέρον αποτέλεσμα όταν πολλαπλασιάζονται. Για παράδειγμα, η μηδενική μήτρα, όπως στην εργασία 2, συζητήθηκε παραπάνω.

Σε πραγματικά προβλήματα, είναι συχνά απαραίτητο να πολλαπλασιάζονται τετράγωνα μήτρες μεγέθους $ \\ left [n \\ times n \\ right] $. Το σύνολο όλων αυτών των πινάκων δηλώνεται με $ ((M) ^ (n)) $ (δηλ. Οι καταχωρίσεις $ A = \\ αριστερά [n \\ times n \\ right] $ και \\ σημαίνει το ίδιο πράγμα) matrix $ E $, το οποίο ονομάζεται μήτρα μονάδας.

Ορισμός Η μήτρα μονάδας μεγέθους $ n $ είναι η μήτρα $ E $ τέτοια ώστε για κάθε τετράγωνο μήτρα $ A = \\ left [n \\ times n \\ right] $ η ισότητα είναι αληθής:

Ένας τέτοιος πίνακας φαίνεται πάντα ο ίδιος: υπάρχουν στην κεντρική διαγώνιο και σε όλα τα άλλα κύτταρα - μηδενικά.

\\ [\\ να αρχίσει (ευθυγράμμιση) & A \\ cdot \\ αριστερά (B + C \\ δεξιά) = A \\ cdot B + A \\ cdot C; \\\\ & \\ αριστερά (A + B \\ δεξιά) \\ cdot C = Α \\ cdot C + B \\ cdot C. \\\\ \\ end (ευθυγράμμιση) \\]

Με άλλα λόγια, εάν χρειάζεται να πολλαπλασιάσετε ένα μήτρα με το άθροισμα των άλλων δύο, μπορείτε να το πολλαπλασιάσετε με κάθε ένα από αυτά τα "δύο άλλα" και στη συνέχεια να προσθέσετε τα αποτελέσματα. Στην πράξη, συνήθως πρέπει να εκτελέσετε την αντίστροφη λειτουργία: παρατηρήστε τον ίδιο πίνακα, βάλτε τον έξω από το βραχίονα, εκτελέστε την προσθήκη και έτσι απλοποιήστε τη ζωή σας :)

Σημείωση: για να περιγράψουμε τη διανομή, έπρεπε να καθορίσουμε δύο τύπους: όπου το άθροισμα βρίσκεται στον δεύτερο πολλαπλασιαστή και όπου το άθροισμα είναι στο πρώτο. Αυτό συμβαίνει ακριβώς επειδή ο πολλαπλασιασμός των πινάκων δεν είναι μεταλλαξιογόνος (και γενικά, στην μη εναλλακτική αλγεβρα υπάρχουν πολλά αστεία που, όταν δουλεύουν με συνηθισμένους αριθμούς, δεν έρχονται καν στο μυαλό). Και αν, για παράδειγμα, πρέπει να ζωγραφίσετε αυτή την ιδιότητα στην εξέταση, να είστε βέβαιος να γράψετε και τους δύο τύπους, αλλιώς ο δάσκαλος μπορεί να πάρει λίγο θυμωμένος.

Λοιπόν, όλα αυτά ήταν τετράγωνα μήτρα ιστορίες. Τι γίνεται με το ορθογώνιο;

Η περίπτωση ορθογωνικών μητρών

Και τίποτα - όλα είναι τα ίδια με αυτά της πλατείας.

Εργασία 3. Εκτέλεση πολλαπλασιασμού:

\\ matrix) \\ begin (matrix) 4 \\\\ 5 \\\\ 1 \\\\\\ τέλος (μήτρα) \\ \\ Η απόφαση. Έχουμε δύο μήτρες: $ A = \\ left [3 \\ times 2 \\ right] $ και $ B = \\ left [2 \\ times 2 \\ right] $. Γράφουμε τους αριθμούς που δηλώνουν τις διαστάσεις στη σειρά:

{!LANG-08a9e41a60216854edddbf930672e7fb!}

Όπως μπορείτε να δείτε, οι δύο κεντρικοί αριθμοί είναι οι ίδιοι. Αυτό σημαίνει ότι οι μήτρες είναι συνεπείς και μπορούν να πολλαπλασιαστούν. Και στην έξοδο παίρνουμε τον πίνακα $ C = \\ left [3 \\ times 2 \\ right] $:

\\ \\ \\ αρχικο (ευθυγραμμιστε) & \\ left [\\ begin (matrix) \\ begin (matrix) 5 \\\\ 2 \\\\ 3 \\\\\\ τέλος (μήτρα) \\ cdot \\ left_ (2 \\ right) +4 \\ cdot 3 & 5 \\ cdot 5 + 4 \\ cdot 4 \\\\ 2 \\ \\ \\ \\ cdot \\ left (-2 \\ right) +5 \\ cdot 3 & 2 \\ cdot 5 + 5 \\ cdot 4 \\\\ 3 \\ cdot \\ left \\ cdot 4 \\\\\\ τέλος (array) \\ right] = \\\\ & = \\ left [\\ begin (array) \\ end (ευθυγράμμιση) \\]

Όλα είναι ξεκάθαρα: στον τελικό πίνακα υπάρχουν 3 σειρές και 2 στήλες. Εντελώς $ = \\ αριστερά [3 \\ φορές 2 \\ δεξιά] $.

Απάντηση: $ \\ left [\\ begin (array)] * (35) (r)) \\ begin (array) \\ begin (μήτρα) 41 \\\\ 30 \\\\ 19 \\\\\\ τέλος (μήτρα) \\\\\\ τέλος (array) \\ right] $.

Τώρα θα εξετάσουμε ένα από τα καλύτερα εκπαιδευτικά καθήκοντα για όσους αρχίζουν να δουλεύουν με πίνακες. Είναι απαραίτητο όχι μόνο να πολλαπλασιαστούν δύο πλάκες, αλλά πρώτα να καθοριστεί: είναι τέτοιος πολλαπλασιασμός αποδεκτός;

Εργασία 4. Βρείτε όλα τα πιθανά ζευγαρωτά προϊόντα των πινάκων:

\\\\]; $ B = \\ αριστερά [\\ begin (matrix) \\ begin (matrix) 0 \\\\ 2 \\\\ 0 \\\\ 4 \\\\\\ τέλος (μήτρα) $ C = \\ left [\\ begin (matrix) 0 & 1 \\\\ 1 & 0 \\\\\\ τέλος (μήτρα) \\ δεξιά] $.

Η απόφαση. Πρώτον, γράφουμε τις διαστάσεις των πινάκων:

\\ B \\ \\ αριστερά [4 \\ φορές 2 \\ δεξιά] \\ C = \\ αριστερά [2 \\ φορές 2 \\ δεξιά] \\]

Παίρνουμε ότι ο matrix $ A $ μπορεί να αντιστοιχιστεί μόνο με το matrix $ B $, αφού ο αριθμός των στηλών στο $ A $ είναι 4 και αυτός ο αριθμός είναι μόνο στο $ B $. Ως εκ τούτου, μπορούμε να βρούμε το προϊόν:

\\\\ cdot \\ left \\ \\ begin (array) (* (35) (r)) 0 & 1 \\\\ 2 & 0 \\\\ 0 & 3 \\\\ 4 & 0 \\\\\\ τέλος (array) Ενδιάμεσα βήματα που προτείνω να εκτελέσετε ο ίδιος ο αναγνώστης. Θα σημειώσω μόνο ότι είναι καλύτερο να καθορίσουμε εκ των προτέρων το μέγεθος του προκύπτοντος πίνακα, πριν από οποιονδήποτε υπολογισμό:

\\\\ cdot \\ αριστερά [4 \\ φορές 2 \\ δεξιά] = \\ αριστερά [2 \\ φορές 2 \\ δεξιά] \\]

Με άλλα λόγια, απλώς καταργούμε τους συντελεστές "διέλευσης" που εξασφάλιζαν τη συνέπεια των πινάκων.

Ποιες άλλες επιλογές είναι δυνατές; Φυσικά, μπορείτε να βρείτε $ B \\ cdot A $, επειδή $ B = \\ left [4 \\ times 2 \\ right] $, $ A = \\ left [2 \\ times 4 \\ right] $, · A \\ right) $ είναι συνεπής και η διάσταση του προϊόντος θα είναι:

{!LANG-6c9a9eee51b20f587700e18f724726ad!}

\\\\ cdot \\ αριστερά [2 \\ φορές 4 \\ δεξιά] = \\ αριστερά [4 \\ φορές 4 \\ δεξιά] \\]

Με λίγα λόγια, η έξοδος θα είναι ο πίνακας $ \\ left [4 \\ times 4 \\ right] $, οι συντελεστές της οποίας μπορούν εύκολα να ληφθούν υπόψη:

\\\\ cdot \\ left \\ \\ begin (array) (* (35) (r)) 1 & -1 & 2 & 8 & -8 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Προφανώς, μπορείτε να συμβιβάσετε ένα άλλο $ C \\ cdot A $ και $ B \\ cdot C $ - αυτό είναι όλο. Επομένως, απλά γράψτε τις εργασίες που προκύπτουν:

Ήταν εύκολο. :)

Απάντηση: $ AB = \\ αριστερά [\\ begin (array)] (* (35) (r)) -10 & 7 \\\\ 10 & 7 \\\\ τέλος (array) \\ right] $; $ BA = \\ left [\\ begin (array) (* (35) (r)) 1 & 1 & 2 & 2 \\ 2 & -2 & 4 & -4 \\\\ 3 & 3 & 6 & 6 \\\\ 4 & -4 & 8 & -8 \\\\\\ τέλος (πίνακας) \\ δικαίωμα] $; $ CA = \\ αριστερά [\\ begin (array) (* (35) (r)) 1 & 1 & 2 & 2 \\\\ 1 άκρο (array) \\ right] $; $ BC = \\ left [\\ begin (array) (* (35) (r)) 1 & 0 \\\\ 0 & 2 \\\\ 3 & 0 \\\\ 0 & 4 \\\\\\ τέλος (array) \\ right] $.

Σε γενικές γραμμές, σας συνιστώ ιδιαίτερα να κάνετε αυτό το έργο από μόνος σας. Και ένα άλλο παρόμοιο έργο που είναι στο σπίτι. Αυτές οι απλές, με την πρώτη ματιά, ανακλάσεις θα σας βοηθήσουν να επεξεργαστείτε όλα τα βασικά στάδια του πολλαπλασιασμού της μήτρας.

Αλλά η ιστορία δεν τελειώνει εκεί. Προχωρούμε στις ειδικές περιπτώσεις πολλαπλασιασμού.

Γραμμή και στήλη Vector

Μία από τις πιο κοινές πράξεις μήτρας είναι ο πολλαπλασιασμός με μια μήτρα στην οποία μία σειρά ή μία στήλη.

Ορισμός Το διάνυσμα στήλης είναι ένας πίνακας μεγέθους $ \\ left [m \\ times 1 \\ right] $, δηλ. που αποτελείται από πολλές σειρές και μόνο από μία στήλη.

Το διάνυσμα σειράς είναι ένας πίνακας μεγέθους $ \\ left [1 \\ times n \\ right] $, δηλ. που αποτελείται από μία σειρά και από μερικές στήλες.

Στην πραγματικότητα, έχουμε ήδη συναντήσει αυτά τα αντικείμενα. Για παράδειγμα, το συνηθισμένο τρισδιάστατο διάνυσμα από stereometry $ \\ overrightarrow (a) = \\ left (x; y; z \\ right) $ δεν είναι τίποτα περισσότερο από ένα διάνυσμα γραμμών. Από την άποψη της θεωρίας, δεν υπάρχει σχεδόν καμία διαφορά μεταξύ των σειρών και των στηλών. Προσοχή πρέπει να είναι εκτός από ότι σε συμφωνία με τους γύρω πολλαπλασιαστές μήτρας.

Εργασία 5. Εκτέλεση πολλαπλασιασμού:

\\ [\\ left \\ \\ begin (array) (* (35) (r)) 2 & -1 & 3 \\\\ 4 & 2 & 0 \\\\ τέλος & \\ cdot \\ left \\ \\ begin (array) (* (35) (r)) 1 \\\\ 2 \\\\ -1 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Η απόφαση. Προς εμάς είναι το προϊόν των αντιστοιχισμένων πινάκων: $ \\ left [3 \\ times 3 \\ right] \\ cdot \\ left [3 \\ times 1 \\ right] = \\ left [3 \\ times 1 \\ right] $. Βρείτε αυτό το κομμάτι:

\\ [\\ left \\ \\ begin (array) (* (35) (r)) 2 & -1 & 3 \\\\ 4 & 2 & 0 \\\\ τέλος & \\ cdot \\ left \\ \\ begin (array) (* (35) (r)) 1 \\\\ 2 \\\\ -1 \\\\\\ τέλος (πίνακας) \\ right] = \\ left [\\ begin ) 2 \\ cdot 1 + 2 \\ cdot 2 + 0 \\ cdot 2 \\ cdot 2 + 2 \\ cdot 2 \\ ) -3 \\\\ 8 \\\\ 0 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Απάντηση: $ \\ left [\\ begin (array) (* (35) (r)) - 3 \\\\ 8 \\\\ 0 \\\\\\ τέλος (πίνακας) \\ δικαίωμα] $.

Εργασία 6. Εκτέλεση πολλαπλασιασμού:

\\ [\\ left \\ \\ start (array) (* (35) (r)) 1 & 2 & -3 \\\\\\ τέλος (array) \\ right] \\ cdot \\ left [ (r)) 3 & 1 & -1 \\\\ 4 & -1 & 3 \\\\ 2 & 6 & 0 \\\\ τέλος (array) \\ right] \\]

Η απόφαση. Και πάλι, όλα συμφωνούνται: $ \\ αριστερά [1 \\ φορές 3 \\ δεξιά] \\ cdot \\ αριστερά [3 \\ φορές 3 \\ δεξιά] = \\ αριστερά [1 \\ φορές 3 \\ δεξιά] $. Θεωρούμε το προϊόν:

\\ [\\ left \\ \\ start (array) (* (35) (r)) 1 & 2 & -3 \\\\\\ τέλος (array) \\ right] \\ cdot \\ left [ (r)) 3 & 1 & -1 \\\\ 4 & -1 & 3 \\\\ 2 & 6 & 0 \\\\ τέλος (array) \\ right] = \\ left [\\ begin (array) r)) 5 & -19 & 5 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Απάντηση: $ \\ left [\\ begin (matrix) 5 & -19 & 5 \\\\\\ τέλος (μήτρα) \\ δεξιά] $.

Όπως μπορείτε να δείτε, όταν πολλαπλασιάζουμε ένα διάνυσμα γραμμών και ένα διάνυσμα στήλης με μια τετραγωνική μήτρα, παίρνουμε πάντα μια γραμμή ή μια στήλη του ιδίου μεγέθους στην έξοδο. Αυτό το γεγονός έχει πολλές εφαρμογές - από την επίλυση γραμμικών εξισώσεων σε διάφορους μετασχηματισμούς συντεταγμένων (οι οποίες τελικά βράζουν και στα συστήματα εξισώσεων, αλλά ας μην μιλήσουμε για λυπημένα πράγματα).

Νομίζω ότι όλα εδώ ήταν προφανή. Επιστρέφουμε στο τελευταίο μέρος του μαθήματος σήμερα.

Αύξηση της μήτρας στην τροφοδοσία

Μεταξύ όλων των πράξεων πολλαπλασιασμού της ατομικής προσοχής αξίζει την εκτόξευση - αυτό είναι όταν πολλαπλασιάζουμε το ίδιο αντικείμενο αρκετές φορές από μόνο του. Οι μήτρες δεν αποτελούν εξαίρεση, μπορούν επίσης να κατασκευαστούν σε διάφορους βαθμούς.

Τα έργα αυτά συντονίζονται πάντοτε:

\\\\ cdot \\ αριστερά [n \\ φορές n \\ right] = \\ left [n \\ times n \\ right] \\]

Και ορίζονται με τον ίδιο τρόπο με τους συνήθεις βαθμούς:

\\ [\\ να αρχίσει (ευθυγράμμιση) & A \\ cdot A = ((A) ^ (2)); \\\\ & A \\ cdot Α \\ cdot Α = ((Α) ^ (3)); \\\\ & \\ υποδίκημα (A \\ cdot A \\ cdot \\ ldots \\ cdot Α) _ (n) = ((A) ^ (n)). \\\\ \\ end (ευθυγράμμιση) \\]

Με την πρώτη ματιά, όλα είναι απλά. Ας δούμε πώς φαίνεται στην πράξη:

Εργασία 7. Ανυψώστε τη μήτρα στην καθορισμένη ισχύ:

$ ((\\ left [\\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right]) ^

Η απόφαση. Λοιπόν, εντάξει, ας οικοδομήσουμε. Πρώτον, ας το τετράγωνο:

\\ n \\ n \\ n \\ n \\ n \\ n \\ n \\ n \\ n \\ n \\ matrix ) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ δεξιά] \\ cdot \\ αριστερά [\\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ 0 \\ cdot 1 + 1 \\ cdot 1 \\\\\\ τέλος (array) \\ right] = \\\\ & = \\ left [\\ begin (array) \\ [\\ begin] \\ (\\ left [\\ begin] \\ begin {\\ start \\ (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right]) ^ (3)) \\ cdot \\ () ()) 1 & 2 \\\\ 0 & 1 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\ cdot \\ left [ \\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right] = \\\\ & Αυτό είναι όλο. :)

Απάντηση: $ \\ left [\\ begin (matrix) 1 & 3 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ δεξιά] $.

Εργασία 8. Ανυψώστε τη μήτρα στην καθορισμένη ισχύ:

\\ \\ ((\\ left [\\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right]) ^ (10)

Η απόφαση. Αλλά τώρα δεν είναι απαραίτητο να φωνάξουμε για το γεγονός ότι "ο βαθμός είναι πολύ μεγάλος", "ο κόσμος δεν είναι δίκαιος" και "οι δάσκαλοι έχουν χάσει εντελώς τις τράπεζες τους". Στην πραγματικότητα, όλα είναι εύκολα:

\\ (\\ αριστερά [\\ begin] 1 & 1 \\\\ 0 & 1 \\\\\\ end (matrix) \\ right]) ^ (10) (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right]) ^ (3)) \\ cdot (\\ left [\\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ cdot \\ αριστερά [\\ begin (matrix) 1 & 1 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ right] = \\\\ & 1 \\\\ 0 τέλος \\ μήκους (δεξιά)] \\ cdot \\ αριστερά (\\ left [ \\ begin (matrix) 1 & 3 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ δεξιά] \\ cdot \\ left [\\ matrix] 1 & 1 \\\\ 0 & 1 \\\\\\ end (matrix) ] \\ right = \\\\ & = \\ left [\\ begin (matrix) 1 & 6 \\\\ 0 & 1 \\\\\\ end (matrix) \\ right] \\ cdot \\ ]

Σημείωση: στη δεύτερη γραμμή χρησιμοποιήσαμε τη συνειδητότητα του πολλαπλασιασμού. Στην πραγματικότητα, το χρησιμοποιήσαμε στην προηγούμενη ανάθεση, αλλά εκεί ήταν σιωπηρή.

Απάντηση: $ \\ left [\\ begin (matrix) 1 & 10 \\\\ 0 & 1 \\\\\\ τέλος (μήτρα) \\ δικαίωμα] $.

Όπως μπορείτε να δείτε, δεν υπάρχει τίποτα δύσκολο να ανεβάσετε το πλέγμα στην εξουσία. Το τελευταίο παράδειγμα μπορεί να συνοψιστεί:

{!LANG-a855fd0ae6a37e70014d7c483f0dbb75!}

{!LANG-f4b1150ac7d24a07bad0672155aa2a15!}

\\ n ()) = \\ left [\\ begin (array)] (* (35) (r)) 1 & n \\ 0 & 1 \\\\\\ τέλος (πίνακας) \\ δεξιά] \\]

Το γεγονός αυτό αποδεικνύεται εύκολα από την μαθηματική επαγωγή ή τον άμεσο πολλαπλασιασμό. Ωστόσο, δεν είναι πάντα δυνατό να πιάσετε τέτοια μοτίβα κατά τη διάρκεια της εκθέσεως. Επομένως, να είστε προσεκτικοί: είναι συχνά πιο εύκολο και πιο γρήγορα να πολλαπλασιάσετε πολλές μήτρες "μπροστά" από το να ψάξετε για οποιαδήποτε μοτίβα.

Σε γενικές γραμμές, μην ψάχνετε για υψηλότερο νόημα όπου δεν υπάρχει κανένας. Συμπερασματικά, θεωρούμε την εκθετήρια μιας μήτρας μεγαλύτερου μεγέθους - όσο και $ \\ αριστερά [3 \\ φορές 3 \\ δεξιά] $.

Εργασία 9. Ανυψώστε τη μήτρα στην καθορισμένη ισχύ:

\\ \\ ((\\ left [\\ begin (matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ end (matrix) \\ right]) ^

Η απόφαση. Δεν θα αναζητήσουμε σχέδια. Δουλεύουμε "μπροστά":

\\ \\ ((\\ left \\ \\ begin (matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ end (matrix) \\ right]) ^ \\ αριστερά [\\ begin (matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ τέλος (μήτρα) \\ right] ^ ^ (μήτρα) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ τέλος (μήτρα) \\ δεξιά] \\]

Πρώτον, ας τετράγωνα αυτό το πλέγμα:

\\ [\\ begin \\ (begin) (\\ matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ end (matrix) \\ right] 2)) = \\ left [\\ begin (matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ τέλος (μήτρα) \\ δεξιά] \\ cdot \\ ) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ τέλος (μήτρα) \\ right] = \\\\ & )) 2 & 1 & 1 \\\\ 1 & 2 & 1 \\\\ 1 & 1 & 2 \\\\ τέλος (πίνακας) \\ δεξιά] \\ τέλος (ευθυγράμμιση) \\]

Τώρα ας φτιάξουμε έναν κύβο:

\\ [\\ begin \\ (begin) (\\ matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ end (matrix) \\ right] 3)) = \\ left [\\ begin (array) (* (35) (r)) 2 & 1 & 1 \\ 1 & 2 & 1 \\\\ 1 & 1 & 2 \\ \\ cdot \\ left [\\ begin (matrix) 0 & 1 & 1 \\\\ 1 & 0 & 1 \\\\ 1 & 1 & 0 \\\\\\ τέλος (μήτρα) \\ right] = \\\\ & array) (* (35) (r)) 2 & 3 & 3 \\ 3 & 2 & 3 \\\\ 3 & 3 & 2 \\\\\\ τέλος (array) \\ right] \\ end (ευθυγράμμιση)

Αυτό είναι όλο. Το πρόβλημα επιλύθηκε.

Απάντηση: $ \\ left [\\ begin (matrix) 2 & 3 & 3 \\ 3 & 2 & 3 \\ 3 & 3 & 2 \\\\\\ end (matrix) \\ right] $.

Όπως μπορείτε να δείτε, το ποσό των υπολογισμών έχει γίνει περισσότερο, αλλά το νόημα δεν έχει αλλάξει καθόλου :)

Στο μάθημα αυτό μπορεί να ολοκληρωθεί. Την επόμενη φορά θα εξετάσουμε την αντίστροφη λειτουργία: για το υπάρχον προϊόν θα αναζητήσουμε τους αρχικούς παράγοντες.

Όπως ίσως μαντέψατε, θα μιλήσουμε για την αντίστροφη μήτρα και τις μεθόδους για την εύρεση της.

Προσθήκη μητρών:

Αφαίρεση και προσθήκη μητρών  μειώνεται στις αντίστοιχες λειτουργίες των στοιχείων τους. Λειτουργία προσθήκης μήτρας εισήχθη μόνο για μήτρες  ίδιο μέγεθος, δηλαδή για μήτρεςτου οποίου ο αριθμός των σειρών και των στηλών είναι αντίστοιχα ίσος. Το άθροισμα των μητρών  Α και Β, που ονομάζονται μήτρα  C, των οποίων τα στοιχεία είναι ίσα με το άθροισμα των αντίστοιχων στοιχείων. C = Α + Β c ij = a ij + b ij διαφορά μήτρας.

Πολλαπλασιασμός μήτρας από τον αριθμό:

Η λειτουργία του πολλαπλασιασμού (διαίρεση) του πίνακα  κάθε μέγεθος με έναν αυθαίρετο αριθμό μειώνεται στον πολλαπλασιασμό (διαίρεση) κάθε στοιχείου μήτρες  σε αυτόν τον αριθμό. Προϊόν Matrix  Και ο αριθμός k καλείται μήτρα  Β έτσι ώστε

b ij = k × a ij. Β = k × A b ij = k × a ij. Matrix  - A = (-1) × A ονομάζεται το αντίθετο μήτρα  Α.

Ιδιότητες προσθήκης μήτρας και πολλαπλασιασμού μήτρας με αριθμό:

Λειτουργίες προσθήκης μήτρας  και πολλαπλασιασμό μήτρας  από τον αριθμό των ακόλουθων ιδιοτήτων: 1. A + B = B + A; 2. Α + (Β + C) = (Α + Β) + C; 3. Α + 0 = Α. 4. Α - Α = 0. 5. 1 × Α = Α. 6. α × (Α + Β) = αΑ + αΒ. 7. (α + β) χ Α = αΑ + βΑ; 8. α × (βA) = (αβ) χ Α. , όπου τα Α, Β και C είναι μήτρες, α και β είναι αριθμοί.

Πολλαπλασιασμός μήτρας (προϊόν Matrix):

Η λειτουργία του πολλαπλασιασμού δύο πινάκων  εισάγεται μόνο για την περίπτωση που ο αριθμός των στηλών είναι ο πρώτος μήτρες  ίσο με τον αριθμό των σειρών δευτερολέπτων μήτρες. Προϊόν Matrix  Και m × n on μήτρα  Σε n × p, καλείται μήτρα  C m × p, ώστε να είναι το άθροισμα των προϊόντων των στοιχείων της i-η γραμμής μήτρες  Και στα αντίστοιχα στοιχεία της στήλης j μήτρες  Β. Εάν μήτρες  Τα τετραγωνίδια Α και Β έχουν το ίδιο μέγεθος, τότε υπάρχουν πάντα τα έργα των ΑΒ και ΒΑ. Είναι εύκολο να δείξουμε ότι A × E = E × A = A, όπου το Α είναι τετράγωνο μήτρα, Ε - μονό μήτρα  με το ίδιο μέγεθος.

Ιδιότητες πολλαπλασιασμού μήτρας:

Πολλαπλασιασμός μήτρας  όχι μεταβλητό, δηλ. AB ≠ VA ακόμα και αν έχουν οριστεί και τα δύο έργα. Ωστόσο, εάν για οποιοδήποτε μήτρες  ο λόγος AB = BA ικανοποιείται, τότε τέτοιος μήτρες  ονομάζονται permutable. Το πιο χαρακτηριστικό παράδειγμα είναι το ενιαίο μήτραη οποία είναι ανάλογη με οποιαδήποτε άλλη με μήτρα  με το ίδιο μέγεθος. Η μετάθεση μπορεί να είναι τετράγωνη μήτρες  της ίδιας τάξης. A × E = E × A = A

Πολλαπλασιασμός μήτρας  έχει τις ακόλουθες ιδιότητες: 1. A × (B × C) = (A × B) × C; 2. Α × (В + С) = АВ + АС; 3. (Α + Β) χ C = AC + BC, 4. α × (ΑΒ) = (αΑ) χ Β. 5. A × 0 = 0. 0 × Α = 0. 6. (ΑΒ) Τ = Β ΤΑΤ; 7. (ΑΒΟ) Τ = ΟΤ Β ΤΑΤ; 8. (Α + Β) Τ = Α Τ + Β Τ.

2. Οι προσδιοριστές της 2ης και 3ης παραγγελίας. Ιδιότητες καθοριστικών παραγόντων.

Ο καθοριστής της μήτρας  δεύτερη σειρά ή καθοριστικός παράγοντας  η δεύτερη σειρά ονομάζεται αριθμός, ο οποίος υπολογίζεται από τον τύπο:

Ο καθοριστής της μήτρας  της τρίτης τάξης ή καθοριστικός παράγοντας η τρίτη τάξη ονομάζεται αριθμός, ο οποίος υπολογίζεται από τον τύπο:

Ο αριθμός αυτός αντιπροσωπεύει ένα αλγεβρικό άθροισμα που αποτελείται από έξι όρους. Κάθε όρος περιέχει ακριβώς ένα στοιχείο από κάθε σειρά και κάθε στήλη. μήτρες. Κάθε προσθήκη αποτελείται από το προϊόν των τριών παραγόντων.

Σημάδια με ποια μέλη προσδιοριστή μήτρας  εισάγετε τον τύπο εύρεση του καθοριστικού παράγοντα της μήτρας  Η τρίτη τάξη μπορεί να καθοριστεί χρησιμοποιώντας το παραπάνω σχήμα, το οποίο ονομάζεται κανόνας των τριγώνων ή ο κανόνας του Σάρρου. Οι τρεις πρώτοι όροι λαμβάνονται με ένα σύμβολο συν και καθορίζονται από το αριστερό σχήμα, και οι επόμενοι τρεις όροι λαμβάνονται με το σύμβολο μείον και καθορίζονται από το σωστό σχήμα.

Προσδιορίστε τον αριθμό των όρων που θα βρείτε προσδιοριστή μήτρας, στο αλγεβρικό άθροισμα, μπορείτε να υπολογίσετε τον παράγοντα: 2! = 1 × 2 = 2 3! = 1 × 2 × 3 = 6

Ιδιότητες καθοριστικών παραγόντων μήτρας

Ιδιότητες καθοριστικών παραγόντων των μητρών:

Αριθμός ακινήτου 1:

Καθοριστικός παράγοντας μήτρας  δεν θα αλλάξει αν οι σειρές του αντικατασταθούν από στήλες, με κάθε σειρά να είναι μια στήλη με τον ίδιο αριθμό και αντίστροφα (Μεταφορά). | A | = | A | Τ

Απόρροια:

Στήλες και σειρές προσδιοριστή μήτρας  ίσες, επομένως, οι ιδιότητες που είναι εγγενείς στις σειρές εκτελούνται για στήλες.

Αριθμός ακινήτου 2:

Κατά την εναλλαγή 2 σειρών ή στηλών προσδιοριστή μήτρας  θα αλλάξει το σημείο στο αντίθετο, διατηρώντας την απόλυτη τιμή, δηλαδή:

Αριθμός ακινήτου 3:

Καθοριστικός παράγοντας μήτρας, που έχει δύο ίδιες σειρές, είναι ίσο με το μηδέν.

Ακίνητα Αρ. 4:

Ο συνολικός πολλαπλασιαστής των στοιχείων μιας σειράς προσδιοριστή μήτρας  μπορεί να αφαιρεθεί για ένα σημάδι καθοριστικός παράγοντας.

Συνέπειες των ιδιοτήτων αριθ. 3 και αριθ. 4:

Αν όλα τα στοιχεία μιας συγκεκριμένης σειράς (σειράς ή στήλης) είναι ανάλογα με τα αντίστοιχα στοιχεία της παράλληλης σειράς, τότε τέτοια προσδιοριστή μήτρας  ισούται με το μηδέν.

Ακίνητα Αρ. 5:

προσδιοριστή μήτρας  ίσο με το μηδέν από τον εαυτό μου προσδιοριστή μήτρας  ισούται με το μηδέν.

Ακίνητα Αρ. 6:

Εάν όλα τα στοιχεία είναι οποιαδήποτε σειρά ή στήλη καθοριστικός παράγοντας  που αντιπροσωπεύεται ως σύνολο 2 στοιχείων, στη συνέχεια καθοριστικός παράγοντας μήτρες  μπορεί να εκπροσωπείται ως άθροισμα 2 καθοριστικούς παράγοντες  σύμφωνα με τον τύπο:

Αρ. Ακινήτου 7:

Αν σε οποιαδήποτε σειρά (ή στη στήλη) καθοριστικός παράγοντας  προσθέστε τα αντίστοιχα στοιχεία μιας άλλης σειράς (ή στήλης) πολλαπλασιασμένης με τον ίδιο αριθμό, στη συνέχεια προσδιοριστή μήτρας  δεν θα αλλάξει το μέγεθός του.

Ένα παράδειγμα χρήσης ιδιοτήτων για τον υπολογισμό προσδιοριστή μήτρας:

1ο έτος, ανώτερα μαθηματικά, μελετάμε μήτρες  και τις κυριότερες ενέργειες σε αυτά. Εδώ συστηματοποιούμε τις βασικές λειτουργίες που μπορούν να πραγματοποιηθούν με μήτρες. Πώς να αρχίσετε να χρονολογείτε με μήτρες; Φυσικά, από τους απλούστερους - ορισμούς, βασικές έννοιες και απλούστερες λειτουργίες. Διαβεβαιώνουμε ότι οι πίνακες θα γίνουν κατανοητοί από όλους όσους θα τους δώσουν τουλάχιστον κάποιο χρόνο!

Ο ορισμός του πίνακα

Matrix  - Αυτός είναι ένας ορθογώνιος πίνακας στοιχείων. Λοιπόν, αν σε απλή γλώσσα - ένας πίνακας αριθμών.

Οι μήτρες συνήθως σημειώνονται με κεφαλαία γράμματα. Για παράδειγμα, η μήτρα Α μήτρα Β   και ούτω καθεξής. Τα πλέγματα μπορούν να έχουν διαφορετικά μεγέθη: ορθογώνια, τετράγωνα, υπάρχουν επίσης σειρές μήτρας και στήλες μήτρας, που ονομάζονται φορείς. Το μέγεθος της μήτρας καθορίζεται από τον αριθμό των σειρών και των στηλών. Για παράδειγμα, γράφουμε μια ορθογώνια μήτρα μεγέθους m   on n όπου m   - ο αριθμός των σειρών και n   - αριθμός στηλών.

Στοιχεία για τα οποία i = j (α11, α22, .. ) αποτελούν την κύρια διαγώνιο της μήτρας και ονομάζονται διαγώνιες.

Τι μπορείτε να κάνετε με τις μήτρες; Προσθήκη / αφαίρεση, πολλαπλασιάζονται με τον αριθμό, πολλαπλασιάζονται μεταξύ τους, μεταφορά. Τώρα για όλες αυτές τις βασικές λειτουργίες σε μήτρες στη σειρά.

Λειτουργίες προσθήκης και αφαίρεσης μήτρας

Προειδοποιείτε αμέσως ότι μπορείτε να προσθέσετε μόνο πλέγματα ίδιου μεγέθους. Το αποτέλεσμα είναι ένας πίνακας του ίδιου μεγέθους. Η προσθήκη (ή αφαίρεση) των πινάκων είναι απλή -   απλώς προσθέστε τα αντίστοιχα στοιχεία τους . Ας δώσουμε ένα παράδειγμα. Εκτελέστε την προσθήκη δύο πινάκων A και B, δύο με δύο.

Η αφαίρεση πραγματοποιείται κατ 'αναλογία, μόνο με το αντίθετο σημείο.

Οποιοσδήποτε αριθμός μπορεί να πολλαπλασιαστεί με έναν αυθαίρετο αριθμό. Για να γίνει αυτό, κάθε στοιχείο πρέπει να πολλαπλασιαστεί με αυτόν τον αριθμό.   Για παράδειγμα, πολλαπλασιάστε τη μήτρα Α από το πρώτο παράδειγμα με τον αριθμό 5:

Λειτουργία πολλαπλασιασμού μήτρας

Πολλαπλασιάζονται μεταξύ τους θα αποτύχουν όλες τις μήτρες. Για παράδειγμα, έχουμε δύο μήτρες, Α και Β. Μπορούν να πολλαπλασιαστούν μεταξύ τους μόνο εάν ο αριθμός των στηλών της μήτρας Α είναι ίσος με τον αριθμό των σειρών της μήτρας Β. Με αυτό τον τρόπο Κάθε στοιχείο του προκύπτοντος πλέγματος στην i-th σειρά και j-th στήλη, θα είναι ίσο με το άθροισμα των γινομένων των αντίστοιχων στοιχείων στο i-th γραμμή του πρώτου πολλαπλασιαστή και j-th στήλη του δεύτερου. Για να κατανοήσουμε αυτόν τον αλγόριθμο, γράφουμε πώς πολλαπλασιάζονται δύο τετράγωνα πλέγματα:

Και ένα παράδειγμα με πραγματικούς αριθμούς. Πολλαπλασιάστε τους πίνακες:

Το Matrix μεταφέρει τη λειτουργία

Η μεταφορά μιας μήτρας είναι μια λειτουργία όταν οι αντίστοιχες σειρές και στήλες ανταλλάσσονται. Για παράδειγμα, μεταφέρετε τη μήτρα Α από το πρώτο παράδειγμα:

Καθοριστικός παράγοντας μήτρας

Ο καθοριστικός παράγοντας και ο καθοριστικός παράγοντας είναι μια από τις βασικές έννοιες της γραμμικής άλγεβρας. Μόλις οι άνθρωποι έρχονται με γραμμικές εξισώσεις, και πίσω τους έπρεπε να εφεύρουν έναν καθοριστικό παράγοντα. Στο τέλος, θα πρέπει να ασχοληθείτε με όλα αυτά, έτσι ώστε η τελευταία ώθηση!

Ο προσδιοριστής είναι ένα αριθμητικό χαρακτηριστικό μιας τετραγωνικής μήτρας, που απαιτείται για την επίλυση πολλών προβλημάτων.
Για να υπολογίσετε τον καθοριστικό παράγοντα της απλού τετραγωνικής μήτρας, πρέπει να υπολογίσετε τη διαφορά μεταξύ των προϊόντων των στοιχείων των κύριων και των δευτερευουσών διαγωνίων.

Ο καθοριστικός παράγοντας της μήτρας της πρώτης τάξης, δηλαδή, που αποτελείται από ένα στοιχείο, είναι ίσος με αυτό το στοιχείο.

Και αν η μήτρα είναι τρία με τρία; Υπάρχει ήδη πιο δύσκολο, αλλά μπορείτε να χειριστείτε.

Για μια τέτοια τιμή της ορίζουσας της μήτρας ισούται με το άθροισμα των γινομένων των στοιχείων των κύρια διαγώνιο και τα προϊόντα των στοιχείων που βρίσκονται στα τρίγωνα με το πρόσωπο παράλληλη προς την κύρια διαγώνιο, από την οποία αφαιρείται το προϊόν από τα διαγώνια στοιχεία των τυχαίων στοιχείων και ξαπλωμένη στο προϊόν με τρίγωνα αντιμετωπίζουν παράλληλο προς το δευτερεύον διαγώνιο.

Ευτυχώς, σπανίως είναι απαραίτητο να υπολογιστούν στην πράξη οι καθοριστικοί παράγοντες των μεγάλων πινάκων.

Εδώ εξετάσαμε τις βασικές λειτουργίες των πινάκων. Φυσικά, στην πραγματική ζωή, δεν μπορείτε ποτέ να βρούμε ούτε έναν υπαινιγμό για ένα σύστημα μήτρας εξισώσεων ή, αντίθετα, μπορεί να συναντήσετε πολύ πιο πολύπλοκες περιπτώσεις όταν πραγματικά πρέπει να σπάσετε το κεφάλι σας. Για τέτοιες περιπτώσεις, υπάρχει ένας επαγγελματίας υπηρεσία φοιτητών  . Ζητήστε βοήθεια, αποκτήστε ποιοτική και λεπτομερή λύση, απολαύστε ακαδημαϊκή επιτυχία και ελεύθερο χρόνο.