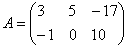Μπορεί η σειρά μήτρα να πολλαπλασιαστεί με έναν αριθμό; Δράσεις μήτρας

Αυτό το εργαλείο θα σας βοηθήσει να μάθετε πώς να εκτελέσετε πράξεις με μήτρες: προσθήκη (αφαίρεση) πινάκων, μεταφορά μήτρας, πολλαπλασιασμός μήτρας, εύρεση αντιστρόφου μήτρας. Το σύνολο του υλικού παρουσιάζεται σε απλή και προσιτή μορφή, παρέχονται σχετικά παραδείγματα, έτσι ώστε ακόμη και ένα απροετοίμαστο άτομο να είναι σε θέση να μάθει πώς να εκτελεί πράξεις με μήτρες. Για τον αυτοέλεγχο και τον αυτοέλεγχο μπορείτε να κατεβάσετε έναν δωρεάν αριθμομηχανή πίνακα \u003e\u003e\u003e.

Θα προσπαθήσω να ελαχιστοποιήσω τους θεωρητικούς υπολογισμούς, σε μερικές περιπτώσεις υπάρχουν εξηγήσεις "στα δάχτυλα" και η χρήση μη επιστημονικών όρων. Οι λάτρεις της στερεάς θεωρίας, παρακαλώ μην ασχολείστε με την κριτική, το καθήκον μας - μάθετε πώς να εκτελείτε ενέργειες με μήτρες.

Για την υπερ-γρήγορη προετοιμασία για το θέμα (που "καίει") υπάρχει ένα εντατικό pdf-course Matrix, καθοριστικός παράγοντας και δοκιμή!

Ο πίνακας είναι ορθογώνιος πίνακας οποιουδήποτε είδους. αντικειμένων. Στην ποιότητα αντικειμένων  θα εξετάσουμε αριθμούς, δηλαδή αριθμητικούς πίνακες. ELEMENT  - αυτός είναι ένας όρος. Ο όρος που είναι επιθυμητό να θυμάστε, θα συμβεί συχνά, δεν είναι τυχαίο ότι χρησιμοποίησα έντονη γραφή για να το επισημάνω.

Ονομασία:  Οι μήτρες συνήθως σημειώνονται με λατινικά γράμματα.

Παράδειγμα:  Εξετάστε τη μήτρα «δύο με τρεις»:

Αυτός ο πίνακας αποτελείται από έξι αντικειμένων:

   Όλοι οι αριθμοί (στοιχεία) μέσα στη μήτρα υπάρχουν από μόνα τους, δηλαδή, δεν υπάρχει θέμα αφαίρεσης:

   Αυτό είναι μόνο ένας πίνακας (σύνολο) αριθμών!

Συμφωνώ επίσης μην αναδιατάξετε  αριθμούς, εκτός εάν αναφέρεται διαφορετικά στις εξηγήσεις. Κάθε αριθμός έχει τη δική του θέση και δεν μπορεί να ανακατευτεί!

Ο εν λόγω πίνακας έχει δύο σειρές:

   και τρεις στήλες:

STANDARD: όταν μιλούν για το μέγεθος της μήτρας, τότε αρχικά  υποδείξτε τον αριθμό των γραμμών και μόνο τότε - τον αριθμό των στηλών. Μόλις ταξινομήσαμε μια μήτρα δύο προς τρεις.

Αν ο αριθμός των γραμμών και των στηλών του πίνακα είναι ο ίδιος, τότε ο πίνακας καλείται τετράγωνογια παράδειγμα:   - μήτρα «τρεις με τρεις».

Εάν η μήτρα είναι μία στήλη ή μία σειρά, τότε καλούνται και αυτές οι μήτρες φορείς.

Στην πραγματικότητα, γνωρίζουμε την έννοια ενός πίνακα από το σχολείο, εξετάστε, για παράδειγμα, ένα σημείο με συντεταγμένες "X" και "Y". Ουσιαστικά, οι συντεταγμένες ενός σημείου γράφονται σε μια μήτρα ενός προς δύο. Με την ευκαιρία, εδώ είναι ένα παράδειγμα γιατί η σειρά των αριθμών έχει σημασία: και - αυτά είναι δύο εντελώς διαφορετικά σημεία του αεροπλάνου.

Τώρα πηγαίνετε απευθείας στη μελέτη δράση με πίνακες:

1) Πράξη ένα. Εκτελώντας το αρνητικό από τη μήτρα (εισάγοντας το πλην στο πλέγμα).

Επιστροφή στο μήτρα μας . Όπως πιθανώς παρατηρήσατε, υπάρχουν πάρα πολλοί αρνητικοί αριθμοί σε αυτόν τον πίνακα. Αυτό είναι πολύ ενοχλητικό από την άποψη της εκτέλεσης διάφορων ενεργειών με το πλέγμα, είναι άβολο να γράψουμε τόσους πολλούς λόγους και μοιάζει άσχημο μόνο στο σχεδιασμό.

Βγάζουμε το αρνητικό από τη μήτρα, αλλάζοντας το σημείο σε ΚΑΘΕ στοιχείο του πίνακα:

   Στο μηδέν, όπως καταλαβαίνετε, το σημείο δεν αλλάζει, το μηδέν είναι μηδενικό στην Αφρική.

Αντίστροφο παράδειγμα: . Φαίνεται άσχημο.

Προσθέτουμε ένα αρνητικό στην μήτρα, αλλάζοντας το σύμβολο κάθε στοιχείου μήτρας:

Λοιπόν, έγινε πολύ καλύτερο. Και, το πιο σημαντικό, η εκτέλεση οποιωνδήποτε ενεργειών με το πλέγμα θα είναι ευκολότερη. Επειδή υπάρχει ένας τέτοιος μαθηματικός λαϊκός χαρακτήρας: τα περισσότερα μειονεκτήματα - τόσο μεγαλύτερη σύγχυση και λάθη.

2) Η δεύτερη ενέργεια. Πολλαπλασιασμός μήτρας με αριθμό.

Παράδειγμα:

Είναι απλό, για να πολλαπλασιάσετε τη μήτρα με αριθμό που χρειάζεστε όλα  στοιχείο μήτρας πολλαπλασιασμένο με τον δεδομένο αριθμό. Στην περίπτωση αυτή, τα τρία πρώτα.

Ένα άλλο χρήσιμο παράδειγμα:

  - πολλαπλασιασμό μήτρας ανά κλάσμα

Πρώτα, σκεφτείτε τι να κάνετε. ΜΗΝ:

   Δεν είναι απαραίτητο να δημιουργηθεί ένα κλάσμα στη μήτρα, καταρχάς, περιπλέκει μόνο τις περαιτέρω ενέργειες με τη μήτρα, δεύτερον, καθιστά δύσκολο για τον εκπαιδευτικό να ελέγξει τη λύση (ειδικά εάν   - την τελική απάντηση του έργου).

Και, επιπλέον, ΜΗΝ  διαιρέστε κάθε στοιχείο της μήτρας με μείον επτά:

Από το άρθρο Μαθηματικά για ανδρείκελα ή από πού να ξεκινήσετε, θυμόμαστε ότι τα δεκαδικά με κόμμα στα ανώτερα μαθηματικά προσπαθούν να αποφύγουν με κάθε δυνατό τρόπο.

Το μόνο πράγμα που επιθυμητή  για να κάνετε αυτό το παράδειγμα είναι να προσθέσετε ένα αρνητικό στην μήτρα:

Αλλά αν Όλα  τα στοιχεία μήτρας διαιρέθηκαν με 7 κανένα υπόλειμμα, τότε θα ήταν δυνατό (και αναγκαίο!) να χωριστούν.

Παράδειγμα:

Σε αυτή την περίπτωση, μπορείτε και μπορείτε ΑΝΑΓΚΗ  πολλαπλασιάστε όλα τα στοιχεία της μήτρας, αφού όλοι οι αριθμοί της μήτρας διαιρούνται με 2 κανένα υπόλειμμα.

Σημείωση: στη θεωρία της ανώτερης μαθηματικών σχολείο έννοια της "διαίρεσης" δεν είναι. Αντί της φράσης "διαιρέστε σε αυτό" μπορείτε πάντα να πείτε "πολλαπλασιάστε με κλάσμα". Δηλαδή, η διαίρεση είναι μια ειδική περίπτωση πολλαπλασιασμού.

3) Η τρίτη ενέργεια. Η μήτρα μεταφέρεται.

Για να μεταφέρετε μια μήτρα, πρέπει να γράψετε τις σειρές της στις στήλες του μετασχηματισμένου πίνακα.

Παράδειγμα:

Μεταφορά μήτρας

Υπάρχει μόνο μία γραμμή και, σύμφωνα με τον κανόνα, θα πρέπει να γραφεί σε μια στήλη:

  - μεταφρασμένη μήτρα.

Ο μετασχηματισμένος πίνακας συνήθως υποδηλώνεται με ένα δείκτη ή μια παύλα στην επάνω δεξιά.

Παράδειγμα βήμα προς βήμα:

Μεταφορά μήτρας

Αρχικά, ξαναγράψουμε την πρώτη σειρά στην πρώτη στήλη:

Μετά ξαναγράψουμε τη δεύτερη σειρά στη δεύτερη στήλη:

Και τέλος, ξαναγράψουμε την τρίτη σειρά στην τρίτη στήλη:

Έχει γίνει. Συνολικά, μεταφέρετε τα μέσα που γυρίζουν τη μήτρα προς την πλευρά.

4) Πράξη τέσσερα. Το άθροισμα (διαφορά) των μητρών.

Το άθροισμα των πινάκων είναι απλό.
   ΔΕΝ ΜΠΟΡΟΥΝ ΝΑ ΠΕΡΙΛΑΜΒΑΝΟΥΝ ΟΛΑ ΤΑ ΥΛΙΚΑ. Για να εκτελέσετε την προσθήκη (αφαίρεση) των πινάκων, είναι απαραίτητο να είναι τα ίδια με το μέγεθος.

Για παράδειγμα, αν δοθεί μια μήτρα "δύο με δύο", τότε μπορεί να προστεθεί μόνο με μία μήτρα "δύο με δύο" και καμία άλλη!

Παράδειγμα:

Προσθέστε μήτρες   και

Για να προσθέσετε τους πίνακες, είναι απαραίτητο να προσθέσετε τα αντίστοιχα στοιχεία τους.:

Για τη διαφορά μήτρας, ο κανόνας είναι παρόμοιος, είναι απαραίτητο να βρεθεί η διαφορά των αντίστοιχων στοιχείων.

Παράδειγμα:

Βρείτε τη διαφορά μήτρας ,

Και πώς να λύσουμε αυτό το παράδειγμα είναι ευκολότερο, έτσι ώστε να μην συγχέεται; Συνιστάται να απαλλαγείτε από τα επιπλέον μειονεκτήματα, γι 'αυτό θα προσθέσουμε ένα αρνητικό στο πλέγμα:

Σημείωση: στη θεωρία της ανώτερης μαθηματικών σχολείο έννοια της "αφαίρεσης" δεν είναι. Αντί της φράσης "αφαιρέστε το από αυτό" μπορείτε πάντα να πείτε "προσθέστε έναν αρνητικό αριθμό σε αυτό". Δηλαδή, η αφαίρεση είναι μια ειδική περίπτωση προσθήκης.

5) Η πέμπτη δράση. Πολλαπλασιασμός μήτρας.

Ποιες μήτρες μπορούν να πολλαπλασιαστούν;

Για να μπορεί ο πίνακας να πολλαπλασιαστεί με τη μήτρα, έτσι ώστε ο αριθμός των στηλών της μήτρας να είναι ίσος με τον αριθμό των σειρών της μήτρας.

Παράδειγμα:
   Είναι δυνατόν να πολλαπλασιάσουμε τη μήτρα με τη μήτρα;

Έτσι μπορείτε να πολλαπλασιάσετε τον πίνακα δεδομένων.

Αλλά αν αναδιαταχθούν οι πίνακες σε κάποια μέρη, τότε, σε αυτή την περίπτωση, ο πολλαπλασιασμός δεν είναι πλέον εφικτός!

Επομένως, είναι αδύνατον να πραγματοποιηθεί πολλαπλασιασμός:

Όχι τόσο σπάνια υπάρχουν εργασίες με ένα τέχνασμα όταν ένας μαθητής καλείται να πολλαπλασιάσει μήτρες των οποίων ο πολλαπλασιασμός είναι προφανώς αδύνατος.

Θα πρέπει να σημειωθεί ότι σε ορισμένες περιπτώσεις είναι δυνατό να πολλαπλασιαστεί η μήτρα και έτσι και έτσι.
   Για παράδειγμα, για μήτρες, και είναι δυνατοί τόσο ο πολλαπλασιασμός όσο και ο πολλαπλασιασμός.

Αριθμός διάλεξης 1

MATRIX

Ορισμός και τύποι πινάκων

Ορισμός 1.1.Με τη μήτραμέγεθος t nονομάζεται ορθογώνιος πίνακας αριθμών (ή άλλων αντικειμένων) που περιέχουν mσειρές και nστήλες.

Τα πλέγματα σημειώνονται με κεφαλαία γράμματα του λατινικού αλφάβητου, για παράδειγμα, A, B, C, ...Εμφανίζονται οι αριθμοί (ή άλλα αντικείμενα) που απαρτίζουν τον πίνακα στοιχείαμήτρες. Τα στοιχεία του πίνακα μπορούν να είναι λειτουργίες. Για να υποδείξετε τα στοιχεία του πίνακα, χρησιμοποιούνται πεζά λατινικά γράμματα με διπλή ευρετηρίαση: aijόπου είναι ο πρώτος δείκτης i(read - and) - αριθμός γραμμής, δεύτερος δείκτης j(διαβάστε - zhi) – αριθμός στήλης.

Ορισμός 1.2.Ο πίνακας καλείται τετράγωνο n-εάν ο αριθμός των σειρών του είναι ίσος με τον αριθμό των στηλών και είναι ίσος με τον ίδιο αριθμό n

Για ένα τετράγωνο πλέγμα, εισάγονται έννοιες. κύρια και πλευράδιαγώνια

Ορισμός 1.3.Κύρια διαγώνιοςΜια τετραγωνική μήτρα αποτελείται από στοιχεία που έχουν τους ίδιους δείκτες, δηλ. Αυτά είναι τα στοιχεία: α11, ένα 22, ...

Ορισμός 1.4. διαγώνια, εάν όλα τα στοιχεία, εκτός από τα στοιχεία της κύριας διαγώνιας, είναι ίσα με το μηδέν

Ορισμός 1.5.Ο τετραγωνικός πίνακας καλείται τριγωνικόαν όλα τα στοιχεία που βρίσκονται κάτω από (ή παραπάνω) η κύρια διαγώνιος είναι ίσα με το μηδέν.

Ορισμός 1.6.Τετραγωνική μήτρα p-η τάξη στην οποία όλα τα στοιχεία της κύριας διαγώνιας είναι ίσα με ένα και τα υπόλοιπα είναι μηδέν, ονομάζεται μόνομε μήτρα nη οποία δηλώνεται από την επιστολή Ε.

Ορισμός 1.7.Ο πίνακας οποιουδήποτε μεγέθους ονομάζεται μηδέν,ή μηδενική μήτρα,αν όλα τα στοιχεία του είναι μηδέν.

Ορισμός 1.8.Ένας πίνακας μίας γραμμής καλείται σειρά μήτρας.

Ορισμός 1.9.Υπολογίζεται ένας μήνας στήλης μήτρα στήλης.

Α = (α11 α12 ... α1n) -μήτρα σειρά?

Ορισμός 1.10.Δύο μήτρες Ακαι Στοτα ίδια μεγέθη καλούνται ίσηεάν όλα τα αντίστοιχα στοιχεία αυτών των μητρών είναι ίσα, δηλ. aij = bijγια οποιονδήποτε i= 1, 2, ..., t; j =1, 2,…, n.

Λειτουργίες μήτρας

Πάνω από τις μήτρες, καθώς και τους παραπάνω αριθμούς, μπορούν να εκτελεστούν διάφορες λειτουργίες. Οι κύριες πράξεις σε μήτρες είναι η προσθήκη (αφαίρεση) των πινάκων, ο πολλαπλασιασμός μιας μήτρας με έναν αριθμό, ο πολλαπλασιασμός των πινάκων. Αυτές οι λειτουργίες είναι παρόμοιες με τις λειτουργίες σε αριθμούς. Μια συγκεκριμένη λειτουργία είναι η μεταφορά της μήτρας.

Πολλαπλασιασμός μήτρας με αριθμό

Ορισμός 1.11.Το προϊόν της μήτρας Α στον αριθμόλ ονομάζεται μήτρα Β = Α,στοιχεία των οποίων λαμβάνονται με τον πολλαπλασιασμό των στοιχείων της μήτρας Ααπό λ .

Παράδειγμα 1.1.Βρείτε το προϊόν Matrix A =   με τον αριθμό 5.

Λύση. . 5Α =

Κανόνας πολλαπλασιασμού μήτρας με αριθμό: για να πολλαπλασιάσετε τον πίνακα με έναν αριθμό, πρέπει να πολλαπλασιάσετε με αυτόν τον αριθμό όλα τα στοιχεία του πίνακα.

Η έρευνα.

1. Ο κοινός παράγοντας όλων των στοιχείων της μήτρας μπορεί να αφαιρεθεί από το σύμβολο της μήτρας.

2. Το προϊόν της μήτρας Αστον αριθμό 0 υπάρχει μηδενική μήτρα: Α· 0 = 0 .

Προσθήκη μήτρας

Ορισμός 1.12.Το άθροισμα των δύο μητρών Α και Βίδιου μεγέθους t nπου ονομάζεται μήτρα Με= Α+ Στοτων οποίων τα στοιχεία λαμβάνονται με την προσθήκη των αντίστοιχων στοιχείων της μήτρας Ακαι μητρών Στοδηλ. cij = aij + bijγια i =1, 2, ..., m; j= 1, 2, ..., n(δηλαδή οι μήτρες προστίθενται στοιχειωδώς).

Η έρευνα.Το άθροισμα της μήτρας Αμε μηδενική μήτρα είναι ίση με την αρχική μήτρα: Α + Ο = Α.

1.2.3. Αφαίρεση μήτρας

Η διαφορά δύο μητρώντο ίδιο μέγεθος καθορίζεται από τις προηγούμενες λειτουργίες: Α - Β = Α + (-1).

Ορισμός 1.13.Matrix -Α = (-1) Αονομάζεται απέναντιμήτρα Α.

Η έρευνα.Το άθροισμα των αντίθετων πινάκων είναι ίσο με το μηδενικό πλέγμα. : Α + (-Α) = Ο.

Πολλαπλασιασμός μήτρας

Ορισμός 1.14.Πολλαπλασιασμός της μήτρας Α με τη μήτρα Βπροσδιορίζεται όταν ο αριθμός των στηλών της πρώτης μήτρας είναι ίσος με τον αριθμό των σειρών της δεύτερης μήτρας. Τότε προϊόν μήτραςονομάζεται τέτοια μήτρα , κάθε στοιχείο του οποίου cijίσο με το άθροισμα των προϊόντων των στοιχείων iμήτρα γραμμών Ασχετικά με τα στοιχεία που ταιριάζουν jμήτρα μήτρας Β.

Παράδειγμα 1.4.Υπολογίστε το προϊόν των πινάκων Α · Β,όπου

A =

=

Παράδειγμα 1.5.Βρείτε Matrix Works ΑΒκαι WA,όπου

Παρατηρήσεις.Από τα παραδείγματα 1.4-1.5 προκύπτει ότι η λειτουργία των πολλαπλασιαστικών πινάκων έχει κάποιες διαφορές από τον πολλαπλασιασμό των αριθμών:

1) εάν το προϊόν των πινάκων ΑΒτότε, μετά την αναδιάταξη των παραγόντων, το προϊόν των πινάκων VAμπορεί να μην υπάρχει. Πράγματι, στο παράδειγμα 1.4 υπάρχει το προϊόν των μήτρων ΑΒ και το προϊόν ΒΑ δεν υπάρχει.

2) ακόμη και αν λειτουργεί ΑΒκαι VAυπάρχουν, το αποτέλεσμα του προϊόντος μπορεί να είναι μήτρες διαφορετικών μεγεθών. Στην περίπτωση που και οι δύο εργασίες ΑΒκαι VAυπάρχουν και οι δύο - πίνακες ίδιου μεγέθους (αυτό είναι δυνατό μόνο όταν πολλαπλασιάζονται τετράγωνα πλέγματα της ίδιας τάξης), τότε ο μεταβαλλόμενος (εναλλάξιμος) νόμος πολλαπλασιασμού δεν είναι ακόμα ικανοποιημένος,δηλ. Α β Στο Α, όπως στο παράδειγμα 1.5;

3) Ωστόσο, εάν πολλαπλασιάσετε ένα τετράγωνο πλέγμα Αανά μονάδα μήτρας Ετην ίδια σειρά ΑΕ = ΕΑ = Α.

Έτσι, όταν πολλαπλασιάζονται οι μήτρες, ο πίνακας ταυτότητας παίζει τον ίδιο ρόλο με τον αριθμό 1 όταν πολλαπλασιάζεται αριθμοί.

4) το προϊόν δύο μη μηκών μητρών μπορεί να είναι ίσο με το μηδενικό πλέγμα, δηλαδή από το γεγονός ότι Α β= 0, αυτό δεν σημαίνει ότι A =0 ή Β =0.

Αυτό το θέμα θα καλύπτει τέτοιες λειτουργίες όπως την προσθήκη και αφαίρεση των πινάκων, τον πολλαπλασιασμό των πινάκων με έναν αριθμό, τον πολλαπλασιασμό της μήτρας με μια μήτρα, τη μεταφορά της μήτρας. Όλοι οι ορισμοί που χρησιμοποιούνται σε αυτή τη σελίδα έχουν ληφθεί από το προηγούμενο θέμα.

  Προσθήκη και αφαίρεση των πινάκων.

Το άθροισμα των πινάκων $ A + B $ $ A_ (m \\ times n) = (a_ (ij)) $ και $ B_ (m \\ φορές n) = (b_ (ij)) $ είναι ο πίνακας $ C_ (m \\ = (c) (ij)), όπου $ c_ (ij) = a_ (ij) + b_ (ij) $ για όλα $ i = \\ overline (1, m) $ και $ j = $.

Παρόμοιος ορισμός εισάγεται για τη διαφορά των μητρών:

Η διαφορά $ AB $ των πινάκων $ A_ (m \\ φορές n) = (a_ (ij)) $ και $ B_ (m \\ φορές n) = (b_ (ij)) $ είναι ο πίνακας $ C_ (m \\ times n) (ij)) $, όπου $ c_ (ij) = a_ (ij) -b_ (ij) $ για όλα $ i = \\ overline (1, m) $ και $ j = \\ overline (1, n) $.

Επεξήγηση της καταχώρησης $ i = \\ overline (1, m) $: εμφάνιση / απόκρυψη

Η καταχώρηση "$ i = \\ overline (1, m) $" σημαίνει ότι η παράμετρος $ i $ κυμαίνεται από 1 έως m. Για παράδειγμα, η καταχώρηση $ i = \\ overline (1,5) $ λέει ότι η παράμετρος $ i $ παίρνει τις τιμές 1, 2, 3, 4, 5.

Αξίζει να σημειωθεί ότι οι λειτουργίες προσθήκης και αφαίρεσης ορίζονται μόνο για μήτρες ίδιου μεγέθους. Γενικά, η προσθήκη και η αφαίρεση των πινάκων είναι πράξεις που είναι διαισθητικά σαφείς, διότι σημαίνουν ουσιαστικά μόνο αθροισμό ή αφαίρεση των αντίστοιχων στοιχείων.

Παράδειγμα №1

Δίδονται τρεις πίνακες:

  $$ A = \\ left (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) \\; \\; B = \\ αριστερά (\\ begin) (πίνακας) (ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 (end (array) \\ right); \\; \\ F = \\ αριστερά (\\ begin (array) (cc) 1 & 0 \\\\ -5 & 4 \\ end (πίνακα) \\ δεξιά). $$

Είναι δυνατή η εύρεση του πίνακα $ A + F $; Βρείτε πίνακες $ C $ και $ D $ αν $ C = A + B $ και $ D = A-B $.

Το $ A $ matrix περιέχει 2 σειρές και 3 στήλες (με άλλα λόγια, το μέγεθος του $ A $ matrix είναι $ 2 \\ φορές $ 3) και το $ F $ matrix περιέχει 2 σειρές και 2 στήλες. Οι διαστάσεις του πίνακα $ A $ και $ F $ δεν συμπίπτουν, επομένως δεν μπορούμε να τις προσθέσουμε, δηλ. η λειτουργία $ A + F $ για αυτές τις μήτρες δεν ορίζεται.

Τα μεγέθη των πινάκων $ A $ και $ B $ είναι τα ίδια, δηλ. Αυτές οι μήτρες περιέχουν ίσο αριθμό σειρών και στηλών, επομένως η λειτουργία προσθήκης ισχύει για αυτούς.

  (Ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) + \\ αριστερά (\\ begin (array) (ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 \\ end (array) \\ right) = \\\\ = \\ left -25) & 1 + 98 \\\\ 5 + 3 & 9 + 0 & -8 + (- 14) \\ end (array) \\ right) = \\ left (\\ ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (πίνακα) \\ δεξιά) $$

Βρείτε τη μήτρα $ D = A-B $:

  $ \\ (Αριστερά) (\\ begin (array) (ccc) -1 & -2 & 1 \\\\ 5 & 9 & -8 \\ end (array) \\ right) (ccc) 10 & -25 & 98 \\\\ 3 & 0 & -14 \\ end (array) \\ right) = \\\\ = \\ left ) & 1-98 \\\\ 5-3 & 9-0 & -8 - (- 14) \\ end (array) \\ right) = \\ left (\\ begin (array) Η απάντηση

: $ C = \\ left (\\ begin (array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ end (array) \\ right) $.  Πολλαπλασιασμός μήτρας με έναν αριθμό.

Το προϊόν της μήτρας $ A_ (m \\ times n) = (a_ (ij)) $ από τον αριθμό $ \\ alpha $ είναι ο πίνακας $ B_ (m \\ times n) = (b_ (ij) \\ alpha \\ cdot α_ (ij) $ για όλα τα $ i = \\ overline (1, m) $ και $ j = \\ overline (1, n) $.

Απλά μιλώντας, για να πολλαπλασιάσετε μια μήτρα με έναν ορισμένο αριθμό σημαίνει να πολλαπλασιάσετε κάθε στοιχείο ενός δεδομένου πίνακα με αυτόν τον αριθμό.

Παράδειγμα 2

{!LANG-179998c46e0a688654372913985c9a9b!}

Ο πίνακας δίνεται: $ A = \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) $. Βρείτε τους πίνακες $ 3 \\ cdot A $, $ -5 \\ cdot A $ και $ -A $.

  $$ 3 \\ cdot A = 3 \\ cdot \\ left (\\ begin (array) (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (ccc) 3 \\ cdot (-1) & 3 \\ cdot (-2) & 3 \\ cdot 7 \\\\ 3 \\ cdot 4 & 3 \\ cdot 9 & 3 \\ cdot 0 \\ \\ left (\\ begin (array) (ccc) -3 & -6 & 21 \\\\ 12 & 27 & 0 \\ end (array) \\ right) \\\\ -5 \\ cdot A = -5 \\ cdot \\ left (ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) = \\ left (\\ cdc) -5 \\ cdot (-1) 5 \\ cdot (-2) & -5 \\ cdot 7 \\\\ -5 \\ cdot 4 & -5 \\ cdot 9 & -5 \\ cdot 0 \\ end (array) \\ right) = \\ left ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ end (array) \\ δεξιά). $$

Η καταχώρηση $ -A $ είναι μια συντετμημένη καταχώρηση για $ -1 \\ cdot A $. Δηλαδή, για να βρείτε $ -A $ πρέπει να πολλαπλασιάσετε όλα τα στοιχεία του matrix $ A $ κατά (-1). Στην ουσία, αυτό σημαίνει ότι το σημείο όλων των στοιχείων του matrix $ A $ θα αλλάξει προς το αντίθετο:

  (Ccc) -1 & -2 & 7 \\\\ 4 & 9 & 0 \\ end (array) \\ right) = \\ cdot A = -1 \\ cdot \\ : $ 3 \\ cdot A = \\ left (\\ begin (array) (ccc) -3 & -6 & 21 \\\\ 12 & 27 & 0 \\ end (array) \\ right); -5 \\ cdot A = \\ αριστερά (\\ begin (array) (ccc) 5 & 10 & -35 \\\\ -20 & -45 & 0 \\ end; -A = \\ left (\\ begin (array) (ccc) 1 & 2 & -7 \\\\ -4 & -9 & 0 \\ end (array) \\ right) $.

: $ C = \\ left (\\ begin (array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ end (array) \\ right) $.  Το προϊόν δύο μητρών.

Ο ορισμός αυτής της ενέργειας είναι δυσκίνητος και, με την πρώτη ματιά, ακατανόητος. Ως εκ τούτου, θα επισημάνω πρώτα έναν γενικό ορισμό και, στη συνέχεια, θα αναλύσω λεπτομερώς τι σημαίνει και πώς να εργαστείτε με αυτό.

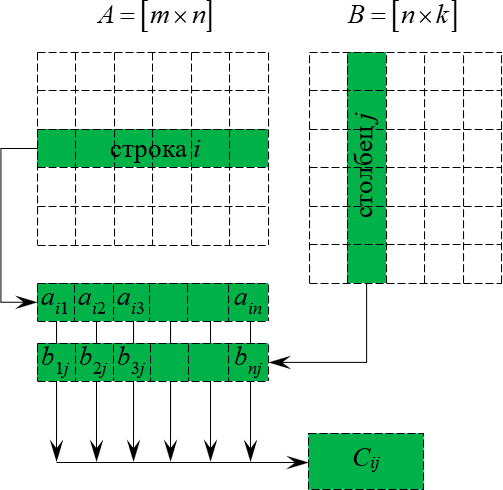
Το προϊόν του μήκους $ A_ (m \\ times n) = (a_ (ij)) $ από τον πίνακα $ B_ (n \\ φορές k) = (b_ (ij)) $ είναι ο πίνακας $ C_ (m \\ times k) ij) $, για το οποίο κάθε στοιχείο του $ c_ (ij) $ είναι ίσο με το άθροισμα των προϊόντων των αντίστοιχων στοιχείων της i-ης γραμμής του πίνακα $ A $ από τα στοιχεία της j-th στήλης της μήτρας $ B $: $$ c_ (ij) = \\ sum \\ limits_ (ρ = 1) ^ (η) a_ (ip) b_ (pj), \\; \\; i = \\ overline (1, m), j = \\ overline (1, n)

Ο πολλαπλασιασμός των πινάκων βήμα προς βήμα θα συζητηθεί με παράδειγμα. Ωστόσο, θα πρέπει να σημειώσετε αμέσως ότι δεν μπορούν να πολλαπλασιαστούν όλες οι μήτρες. Αν θέλουμε να πολλαπλασιάσουμε τον πίνακα $ A $ με το matrix $ B $, τότε πρέπει πρώτα να βεβαιωθούμε ότι ο αριθμός των στηλών του matrix $ A $ είναι ίσος με τον αριθμό των γραμμών του πίνακα $ B $ (οι εν λόγω πίνακες καλούνται συχνά

συμφώνησε {!LANG-69f0e6da9be87b2fd3d70d6670655bd5!}). Για παράδειγμα, ο πίνακας $ A_ (5 \\ φορές 4) $ (ο πίνακας περιέχει 5 σειρές και 4 στήλες) δεν μπορεί να πολλαπλασιαστεί με τον πίνακα $ F_ (9 φορές 8) $ (9 σειρές και 8 στήλες), αφού ο αριθμός των στηλών του πίνακα $ A Το $ δεν είναι ίσο με τον αριθμό των σειρών του πίνακα $ F $, δηλ. $ 4 \\ neq 9 $. Μπορούμε όμως να πολλαπλασιάσουμε το matrix $ A_ (5 \\ times 4) $ με το matrix $ B_ (4 \\ times 9) $, αφού ο αριθμός των στηλών του πίνακα $ A $ είναι ίσος με τον αριθμό των γραμμών του πίνακα $ B $. Το αποτέλεσμα του πολλαπλασιασμού των πινάκων $ A_ (5 \\ φορές 4) $ και $ B_ (4 \\ φορές 9) $ είναι ο πίνακας $ C_ (5 \\ φορές 9) $, που περιέχει 5 σειρές και 9 στήλες:

Παράδειγμα 3

Οι μήτρες καθορίζονται: $ A = \\ left (\\ begin (array) (cccc) -1 & 2 & -3 & 0 \\ 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & -5 (array) \\ right) $ και $ B = \\ left (\\ begin (array) (cc) -9 & 3 \\\\ 6 & 20 \\ 7 & 0 \\\\ 12 & -4 \\ $. Βρείτε τη μήτρα $ C = A \\ cdot B $.

Αρχικά, καθορίζουμε αμέσως το μέγεθος του πίνακα $ C $. Δεδομένου ότι ο πίνακας $ A $ έχει μέγεθος $ 3 \\ φορές 4 $ και ο πίνακας $ B $ έχει μέγεθος $ 4 \\ φορές $ 2, το μέγεθος του πίνακα $ C $ έχει ως εξής: $ 3 \\ φορές 2 $:

Έτσι, ως αποτέλεσμα του προϊόντος των πινάκων $ A $ και $ B $ πρέπει να έχουμε τον πίνακα $ C $ που αποτελείται από τρεις σειρές και δύο στήλες: $ C = \\ left (\\ begin (array) (cc) c_ (11) & c_ 12) \\\\ c_ (21) & c_ (22) \\\\ c_ (31) & c_ (32) \\ τέλος (πίνακας) \\ δεξιά) $. Εάν οι προσδιορισμοί των στοιχείων προκαλούν ερωτήσεις, τότε μπορείτε να δείτε το προηγούμενο θέμα: "Τύποι μήτρων" Βασικοί όροι "  , στην αρχή του οποίου εξηγείται ο προσδιορισμός των στοιχείων της μήτρας. Ο στόχος μας: να βρούμε τις τιμές όλων των στοιχείων του πίνακα $ C $.

Ας ξεκινήσουμε με το στοιχείο $ c_ (11) $. Για να πάρετε το στοιχείο $ c_ (11) $ πρέπει να βρείτε το άθροισμα των προϊόντων των στοιχείων της πρώτης γραμμής του πίνακα $ A $ και της πρώτης στήλης του πίνακα $ B $:

Για να βρεθεί το ίδιο το $ c_ (11) $, είναι απαραίτητο να πολλαπλασιάσουμε τα στοιχεία της πρώτης γραμμής του πίνακα $ A $ με τα αντίστοιχα στοιχεία της πρώτης στήλης του πίνακα $ B $, δηλ. το πρώτο στοιχείο για το πρώτο, το δεύτερο για το δεύτερο, το τρίτο για το τρίτο, το τέταρτο για το τέταρτο. Τα αποτελέσματα συνοψίζονται:

  $$ c_ (11) = - 1 \\ cdot (-9) + 2 \\ cdot 6 + (- 3) \\ cdot 7 + 0 \\ cdot 12 = 0. $$

Συνεχίστε τη λύση και βρείτε $ c_ (12) $. Για να γίνει αυτό, πρέπει να πολλαπλασιάσετε τα στοιχεία της πρώτης γραμμής του πίνακα $ A $ και τη δεύτερη στήλη του πίνακα $ B $:

Παρόμοια με την προηγούμενη, έχουμε:

  $$ c_ (12) = - 1 \\ cdot 3 + 2 \\ cdot 20 + (- 3) \\ cdot 0 + 0 \\ cdot (-4) = 37. $$

Όλα τα στοιχεία της πρώτης γραμμής του πίνακα $ C $ βρίσκονται. Γυρίζουμε στη δεύτερη γραμμή, η οποία ξεκινά το στοιχείο $ c_ (21) $. Για να το βρείτε πρέπει να πολλαπλασιάσετε τα στοιχεία της δεύτερης σειράς του πίνακα $ A $ και την πρώτη στήλη του πίνακα $ B $:

  $$ c_ (21) = 5 \\ cdot (-9) +4 \\ cdot 6 + (- 2) \\ cdot 7 + 1 \\ cdot 12 = -23. $$

Το επόμενο στοιχείο $ c_ (22) $ βρίσκεται με τον πολλαπλασιασμό των στοιχείων της δεύτερης γραμμής του πίνακα $ A $ με τα αντίστοιχα στοιχεία της δεύτερης στήλης του πίνακα $ B $:

  $$ c_ (22) = 5 \\ cdot 3 + 4 \\ cdot 20 + (- 2) \\ cdot 0 + 1 \\ cdot (-4) = 91. $$

Για να βρούμε $ c_ (31) $ πολλαπλασιάζουμε τα στοιχεία της τρίτης γραμμής του πίνακα $ A $ με τα στοιχεία της πρώτης στήλης του πίνακα $ B $:

  $$ c_ (31) = - 8 \\ cdot (-9) +11 \\ cdot 6 + (- 10) \\ cdot 7 + (-5) \\ cdot 12 = 8. $$

Και, τέλος, για να βρούμε το στοιχείο $ c_ (32) $, πρέπει να πολλαπλασιάσουμε τα στοιχεία της τρίτης γραμμής του πίνακα $ A $ με τα αντίστοιχα στοιχεία της δεύτερης στήλης του πίνακα $ B $:

  $$ c_ (32) = - 8 \\ cdot 3 + 11 \\ cdot 20 + (- 10) \\ cdot 0 + (-5) \\ cdot (-4) = 216. $$

Όλα τα στοιχεία του πίνακα $ C $ βρίσκονται, μόνο για να καταγράψουμε ότι $ C = \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) . Ή, εάν έχετε ήδη γράψει πλήρως:

  (Cccc) -1 & 2 & -3 & 0 & 5 & 4 & -2 & 1 \\\\ -8 & 11 & -10 & - 5 \\ end (array) \\ right) \\ cdot \\ left (\\ begin (array) (cc) -9 & 3 \\\\ 6 & 20 \\\\ 7 & 0 \\\\ 12 & -4 \\ = \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right). $$

: $ C = \\ left (\\ begin (array) (ccc) 9 & -27 & 99 \\\\ 8 & 9 & -22 \\ end (array) (ccc) -11 & 23 & -97 \\\\ 2 & 9 & 6 \\ end (array) \\ right) $.: $ C = \\ left (\\ begin (array) (cc) 0 & 37 \\\\ -23 & 91 \\\\ 8 & 216 \\ end (array) \\ right) $.

Παρεμπιπτόντως, δεν υπάρχει συχνά λόγος να περιγραφεί λεπτομερώς η διαπίστωση κάθε στοιχείου του πίνακα αποτελεσμάτων. Για τις μήτρες των οποίων το μέγεθος είναι μικρό, μπορείτε να το κάνετε αυτό:

Αξίζει επίσης να σημειωθεί ότι ο πολλαπλασιασμός των μητρών δεν είναι μεταλλαξιογόνος. Αυτό σημαίνει ότι στη γενική περίπτωση $ A \\ cdot B \\ neq B \\ cdot A $. Μόνο για ορισμένους τύπους μήτρων που ονομάζονται permutable  (ή μετακίνηση), η ισότητα $ A \\ cdot B = B \\ cdot A $ είναι αληθής. Βασίζεται στην μη μεταλλαξιμότητα του πολλαπλασιασμού που απαιτείται να υποδείξει τον τρόπο με τον οποίο πολλαπλασιάζουμε την έκφραση με ένα ή άλλο πίνακα: δεξιά ή αριστερά. Για παράδειγμα, η φράση "πολλαπλασιάστε τις δύο πλευρές της ισότητας $ 3E-F = Y $ από το matrix $ A $ στα δεξιά" σημαίνει ότι πρέπει να αποκτήσουμε την ακόλουθη ισότητα: $ (3E-F) \\ cdot A = Y \\ cdot A $.

Μετασχηματίζεται σε σχέση με τη μήτρα $ A_ (m \\ times n) = (a_ (ij)) $ ονομάζεται μήτρα $ A_ (n \\ φορές m) ^ (T) = (a_ (ij) ^ (T) που $ a_ (ij) ^ (T) = a_ (ji) $.

Με απλά λόγια, για να φτάσετε στο μετασχηματισμένο πλέγμα $ A ^ T $, πρέπει να αντικαταστήσετε τις στήλες στον αρχικό πίνακα $ A $ με τις αντίστοιχες σειρές σύμφωνα με αυτή την αρχή: εάν η πρώτη σειρά ήταν, η πρώτη στήλη θα ήταν. ήταν η δεύτερη σειρά - θα γίνει η δεύτερη στήλη. υπήρχε μια τρίτη σειρά - θα υπήρχε μια τρίτη στήλη και ούτω καθεξής. Για παράδειγμα, ας βρούμε ένα μετασχηματισμένο πλέγμα στο matrix $ A_ (3 \\ φορές 5) $:

Συνεπώς, εάν ο αρχικός πίνακας είχε μέγεθος $ 3 \\ φορές $ 5, τότε ο μετασχηματισμένος πίνακας έχει μέγεθος $ 5 \\ φορές $ 3.

  Ορισμένες ιδιότητες των πράξεων σε μήτρες.

Εδώ υποτίθεται ότι τα $ \\ alpha $, $ \\ beta $ είναι μερικοί αριθμοί και $ A $, $ B $, $ C $ είναι πίνακες. Για τις τέσσερις πρώτες ιδιότητες έδειξα τα ονόματα, τα υπόλοιπα μπορούν να κληθούν κατ 'αναλογία με τα πρώτα τέσσερα.

1. $ A + B = B + A $ (μεταβλητότητα προσθήκης)
2. $ A + (B + C) = (Α + Β) + C $ (προστιθέμενη προστιθέμενη αξία)
3. $ (\\ alpha + \\ beta) \\ cdot A = \\ alpha A + \\ beta A $ (κατανομή πολλαπλασιασμού από μια μήτρα σε σχέση με την προσθήκη αριθμών)
4. $ \\ alpha \\ cdot (A + B) = \\ alpha A + \\ alpha B $ (κατανομή πολλαπλασιασμού με τον αριθμό σε σχέση με την προσθήκη πινάκων)
5. $ A (BC) = (ΑΒ) C $
6. $ (\\ alpha \\ beta) Α = \\ άλφα (\\ beta A) $
7. $ A \\ cdot (B + C) = AB + AC $, $ (Β + Γ) \\ cdot A = BA + CA $.
8. $ A \\ cdot E = A $, $ E \\ cdot A = A $, όπου $ E $ είναι ο πίνακας ταυτότητας της αντίστοιχης παραγγελίας.
9. $ A \\ cdot O = O $, $ O \\ cdot A = O $, όπου $ O $ είναι η μηδενική μήτρα του αντίστοιχου μεγέθους.
10. $ \\ αριστερά (A ^ T \\ δεξιά) ^ T = A $
11. $ (Α + Β) ^ Τ = Α ^ Τ + Β ^ Τ $
12. $ (AB) ^ T = B ^ T \\ cdot A ^ T $
13. $ \\ αριστερά (\\ alpha A \\ right) ^ T = \\ alpha A ^ T $

Στο επόμενο μέρος, θα εξετάσουμε τη λειτουργία της ανύψωσης της μήτρας σε έναν μη αρνητικό ακέραιο βαθμό και επίσης θα επιλύσουμε παραδείγματα στα οποία θα απαιτηθούν διάφορες λειτουργίες σε μήτρες.