Επίλυση της καθήκης παραγωγής σε μια μέθοδο πίνακα απλού. Λύση συστημάτων γραμμικών εξισώσεων από την Jordan-Gauss

Εξετάστε την απόφαση της μεθόδου Simplex ZLP και το δηλώστε σε σχέση με το έργο μεγιστοποίησης.

1. Με την προϋπόθεση του προβλήματος, το μαθηματικό μοντέλο της καταρτίζεται.

2. Το σχεδιασμένο μοντέλο μετατρέπεται σε κανονική μορφή. Αυτό μπορεί να επιλέξει τη βάση με το αρχικό σχέδιο στήριξης.

3. Το κανονικό μοντέλο της εργασίας είναι γραμμένο με τη μορφή πίνακα απλού μέσου έτσι ώστε όλα τα ελεύθερα μέλη να είναι μη αρνητικά. Εάν το αρχικό σχέδιο στήριξης κατανέμεται, στη συνέχεια, μεταβείτε στη ρήτρα 5.

Πίνακας Simplex: Το σύστημα περιοριστικών εξισώσεων και λειτουργίας στόχου με τη μορφή εκφράσεων επιτρέπονται σε σχέση με την αρχική βάση. Η συμβολοσειρά στην οποία οι παράγοντες της λειτουργίας στόχου F γράφονται στη συμβολοσειρά F ή μια σειρά της λειτουργίας στόχου.

4. Βρείτε ένα αρχικό σχέδιο αναφοράς, παραγωγή απλών μετασχηματισμών με θετικά στοιχεία επίλυσης που πληρούν τις ελάχιστες σχέσεις απλού και χωρίς να λαμβάνουν υπόψη τα σημάδια των στοιχείων της συμβολοσειράς F. Εάν πληρούται μια συμβολοσειρά 0 κατά τη διάρκεια των μετασχηματισμών, όλα τα στοιχεία των οποίων, εκτός από ένα ελεύθερο μέλος, μηδενικά, τότε το σύστημα περιοριστικών εξισώσεων του προβλήματος είναι ακατανόητο. Εάν πληρούται μια συμβολοσειρά 0 στην οποία, εκτός από ένα ελεύθερο μέλος, δεν υπάρχουν άλλα θετικά στοιχεία, το σύστημα περιοριστικών εξισώσεων δεν έχει μη αρνητικές λύσεις.

Η ένδειξη του συστήματος (2.55), (2.56) σε μια νέα βάση θα ονομάζεται Simplex μετασχηματισμός. Εάν ο μετασχηματισμός Simplex θεωρείται ως επίσημη αλγεβρική λειτουργία, τότε μπορεί να σημειωθεί ότι ως αποτέλεσμα αυτής της λειτουργίας, οι ρόλοι ανακατανεμηθούν μεταξύ δύο μεταβλητών που περιλαμβάνονται σε κάποιο σύστημα γραμμικές λειτουργίες: Μία μεταβλητή από τις εξαρτημένες αλλαγές στον ανεξάρτητο και το άλλο αντίθετο - από ανεξάρτητο από τον εξαρτώμενο. Μια τέτοια ενέργεια είναι γνωστή στην άλγεβρα που ονομάζεται εξαίρεση του Schardan.

5. Εξετάζεται το αρχικό σχέδιο αναφοράς για τη βελτιστοποίηση:

α) Εάν δεν υπάρχουν αρνητικά στοιχεία στη γραμμή F (χωρίς να υπολογίζετε το ελεύθερο μέλος), το σχέδιο είναι βέλτιστο. Εάν δεν υπάρχει μηδέν, τότε το βέλτιστο σχέδιο είναι το μόνο. Εάν υπάρχουν τουλάχιστον ένα μηδέν, τότε τα βέλτιστα σχέδια είναι άπειρα σετ.

β) Εάν υπάρχει τουλάχιστον ένα αρνητικό στοιχείο στη γραμμή F στην οποία αντιστοιχεί η στήλη εισβολής στοιχείου,<

γ) Εάν υπάρχει τουλάχιστον ένα αρνητικό στοιχείο στη γραμμή F και στη στήλη του υπάρχει τουλάχιστον ένα θετικό, τότε μπορείτε να πάτε σε ένα νέο σχέδιο αναφοράς, πιο κοντά στο βέλτιστο. Για να το κάνετε αυτό, η καθορισμένη στήλη πρέπει να εκχωρηθεί σε άδεια, με ελάχιστη σχέση απλού μέσου για να βρείτε την επιτόπια συμβολοσειρά και να εκτελέσει simplex μετατροπή. Το προκύπτον σχέδιο αναφοράς εξετάζεται και πάλι για τη βελτιστοποίηση. Η περιγραφείσα διαδικασία επαναλαμβάνεται μέχρις ότου ληφθεί το βέλτιστο σχέδιο ή πριν από την καθιέρωση της ασταθής του προβλήματος.

Η στήλη των συντελεστών με μια μεταβλητή που περιλαμβάνεται στη βάση ονομάζεται επιτρεπτή. Έτσι, η επιλογή μιας μεταβλητής που εισάγεται στη βάση (ή η επιλογή της στήλης που επιτρέπει) σε ένα αρνητικό στοιχείο της γραμμής F, εξασφαλίζουμε την αυξανόμενη λειτουργία F.

Λίγο πιο δύσκολο καθορίζεται από τη μεταβλητή που πρέπει να αποκλειστεί από τη βάση. Για να γίνει αυτό, η σχέση των ελεύθερων μελών στα θετικά στοιχεία της στήλης ανάλυσης (τέτοιες σχέσεις ονομάζεται Simplex) και βρίσκει μεταξύ τους το μικρότερο, το οποίο καθορίζει τη συμβολοσειρά (επιτρέποντας) που περιέχει την αποκλειστική μεταβλητή. Η επιλογή μιας μεταβλητής που εξαιρείται από τη βάση (ή η επιλογή της γραμμής επίλυσης) είναι εγγυημένη από τον ελάχιστο λόγο απλού συστήματος, όπως ήδη καθιερώνεται, η θετικότητα των βασικών στοιχείων σε ένα νέο σχέδιο αναφοράς.

Στην παράγραφο 3 του αλγορίθμου θεωρείται ότι όλα τα στοιχεία της στήλης των ελεύθερων μελών είναι μη αρνητικές. Αυτή η απαίτηση δεν είναι απαραίτητη, αλλά αν ολοκληρωθεί, όλοι οι μεταγενέστεροι μετασχηματιστές απλών αποβλήτων γίνονται μόνο με θετικά στοιχεία επίλυσης, τα οποία είναι βολικά κατά τον υπολογισμό. Εάν υπάρχουν αρνητικοί αριθμοί στη στήλη των ελεύθερων μελών, το στοιχείο ανάλυσης επιλέγεται ως εξής:

1) Προβάλετε μια συμβολοσειρά που πληροί οποιοδήποτε αρνητικό ελεύθερο μέλος, για παράδειγμα μια γραμμή T και επιλέξτε οποιοδήποτε αρνητικό στοιχείο σε αυτό και η στήλη που αντιστοιχεί σε αυτό λαμβάνεται για το επιτρεπτό (υποθέτουμε ότι οι περιορισμοί της εργασίας είναι από κοινού).

2) συνθέτουν τη σχέση στοιχείων της στήλης των ελεύθερων μελών στα αντίστοιχα στοιχεία της στήλης ανάλυσης, έχοντας τα ίδια σημάδια (simplex σχέσεις).

3) Από τις simplex σχέσεις επιλέγουν το μικρότερο. Θα καθορίσει τη συμβολοσειρά. Αφήστε το να είναι, για παράδειγμα, p εγκεφαλικό επεισόδιο.

4) Στη διασταύρωση της στήλης ανάλυσης και οι γραμμές είναι το επιτρεπόμενο στοιχείο. Εάν επιτρέπεται ένα στοιχείο I-line, στη συνέχεια, μετά τη μετατροπή του Simplex, το ελεύθερο μέλος αυτής της γραμμής θα γίνει θετικό. Διαφορετικά, στο επόμενο βήμα, γυρίστε στη γραμμή Τ. Εάν η εργασία είναι επιλυτική, τότε ένας ορισμένος αριθμός βημάτων στη στήλη των ελεύθερων μελών δεν θα παραμείνει αρνητικά στοιχεία.

Βρίσκοντας το αρχικό σχέδιο στήριξης, ο κανονικός τύπος ZLP

Η ιδέα μιας συνεπούς λύσης βελτίωσης βασίστηκε σε μια καθολική μέθοδο επίλυσης μιας γραμμικής μεθόδου απλού προγραμματισμού - της μεθόδου απλού ομίλου ή μιας σταθερής μεθόδου μεθόδου βελτίωσης.

Η γεωμετρική έννοια της μεθόδου απλού συστήματος συνίσταται σε μια διαδοχική μετάβαση από μία κορυφή των περιορισμών ορίου πολυεδρονίου (που ονομάζεται αρχικός) στους γειτονικούς, στο οποίο η γραμμική λειτουργία παίρνει το καλύτερο (τουλάχιστον όχι η χειρότερη) τιμή σε σχέση με τον στόχο του πρόβλημα; Όσο βρεθεί η βέλτιστη λύση - η κορυφή, όπου επιτυγχάνεται η βέλτιστη τιμή της λειτουργίας στόχου (εάν η εργασία έχει την τελική βέλτιστη).

Για πρώτη φορά, η μέθοδος Simplex προτάθηκε από τον Αμερικανό επιστήμονα J. Danzig το 1949, αλλά το 1939 οι ιδέες της μεθόδου αναπτύχθηκαν από τους Ρώσους επιστήμονες L.V. Kantorovich.

Μέθοδος Simplex που σας επιτρέπει να λύσετε οποιαδήποτε εργασία γραμμικού προγραμματισμού, καθολική. Επί του παρόντος, χρησιμοποιείται για υπολογισμούς υπολογιστών, όσο απλά απλά παραδείγματα που χρησιμοποιούν τη μέθοδο Simplex μπορούν να λυθούν με το χέρι.

Για να εφαρμόσετε τη μέθοδο Simplex - μια συνεπής βελτίωση της λύσης - είναι απαραίτητο να κυριαρχήσει τρία βασικά στοιχεία:

Μια μέθοδο για τον προσδιορισμό κάθε αρχικής παραδεκτής βασικής λύσης του προβλήματος.

Κανόνας μετάβασης για το καλύτερο (ακριβέστερα, όχι το χειρότερο) λύση.

Κριτήριο για τον έλεγχο της βέλτιστης λειτουργίας της λύσης που βρέθηκε.

Για να χρησιμοποιήσετε τη μέθοδο Simplex, το πρόβλημα γραμμικού προγραμματισμού πρέπει να χορηγείται σε κανονική μορφή, δηλ. Το σύστημα περιορισμών πρέπει να εκπροσωπείται με τη μορφή εξισώσεων.

Η βιβλιογραφία περιγράφει λεπτομερώς: την εξεύρεση του αρχικού σχεδίου αναφοράς (αρχική έγκυρη λύση βάσης), επίσης - με τη μέθοδο τεχνητής βάσης, εξεύρεση του βέλτιστου σχεδίου αναφοράς, επίλυση εργασιών που χρησιμοποιούν πίνακες Simplex.

58. Το κύριο θεώρημα του συμβόλου της μεθόδου.

???????????????????????????????????????????????????????????????????????

59. Εναλλακτική λύση στο ZLP, DEGENERACY σε ZLP.

Εκφυλισμός γραμμικών εργασιών προγραμματισμού

Λαμβάνοντας υπόψη τη μέθοδο Simplex, υποθέσαμε ότι το πρόβλημα του γραμμικού προγραμματισμού είναι μη μηδενικό, δηλ. Κάθε σχέδιο αναφοράς περιέχει ομαλά m θετικά εξαρτήματα, όπου m είναι ο αριθμός των περιορισμών στο πρόβλημα. Σε ένα εκφυλισμένο σχέδιο αναφοράς, ο αριθμός των θετικών εξαρτημάτων αποδεικνύεται μικρότερος από τον αριθμό των περιορισμών: ορισμένες βασικές μεταβλητές που αντιστοιχούν σε αυτό το σχέδιο αναφοράς λαμβάνουν μηδενικές τιμές. Χρησιμοποιώντας τη γεωμετρική ερμηνεία για την απλούστερη περίπτωση, όταν n - m \u003d 2 (ο αριθμός των μεταβλητών που δεν αποσυνδέονται είναι 2), διακρίνεται εύκολα από μια εκφυλισμένη εργασία από το μηδενικό. Στο εκφυλισμένο πρόβλημα σε μια κορυφή του πολυεδρού, περισσότερες από δύο άμεσες γραμμές που περιγράφονται από τις εξισώσεις του σχήματος XI \u003d 0 είναι τέσσερις. Αυτό σημαίνει ότι μία ή περισσότερες πλευρές των συνθηκών πολυγώνου σφίγγονται στο σημείο. Ομοίως, στο N-M \u003d 3, περισσότερα από 3 επίπεδα Xi \u003d 0 διασταυρώνονται στο εκφυλισμένο πρόβλημα σε μία κορυφή. Υπό την παραδοχή της μη εκφυλισμένης εργασίας

Υπήρξε μόνο μία τιμή, η οποία καθόρισε τον δείκτη των συνθηκών που έχουν κατατεθεί από τη βάση του φορέα (που προέρχεται από τη βασική μεταβλητή). ΣΕ

Η εκφυλισμένη εργασία μπορεί να επιτευχθεί σε αρκετούς δείκτες ταυτόχρονα (για αρκετές γραμμές). Σε αυτή την περίπτωση, σε ένα σχέδιο αναφοράς, αρκετές βασικές μεταβλητές θα είναι μηδέν. Εάν το πρόβλημα του γραμμικού προγραμματισμού αποδειχθεί εκφυλισμένο, τότε με μια κακή επιλογή του φορέα των συνθηκών που προέρχονται από τη βάση, μπορεί να εμφανιστεί μια άπειρη κίνηση σε βάσεις του ίδιου σχεδίου αναφοράς. Αυτό είναι το λεγόμενο φαινόμενο ζουμερό. Παρόλο που στα πρακτικά καθήκοντα του γραμμικού προγραμματισμού, ο βρόχος είναι μάλλον σπάνιο, δεν αποκλείεται. Μία από τις μεθόδους καταπολέμησης του εκφυλισμού είναι η μετατροπή του προβλήματος από τις "ασήμαντες" αλλαγές στα σωστά μέρη του συστήματος περιορισμών κατά μέγεθος κατά τρόπο ώστε το έργο να έχει γίνει μη μηδενικό και, ταυτόχρονα, ότι αυτή η αλλαγή κάνει δεν επηρεάζουν το βέλτιστο σχέδιο εργασιών. Πιο συχνά, οι εφαρμοζόμενοι αλγόριθμοι περιλαμβάνουν ορισμένους απλούς κανόνες που μειώνουν την πιθανότητα βρόχου ή ξεχασμένης. Αφήστε τη μεταβλητή XJ να είναι απαραίτητη για να γίνει η βάση. Σκεφτείτε

Πολλαπλοί δείκτες E0, που αποτελούνται από αυτά τα i για τα οποία επιτυγχάνεται. Πολλοί δείκτες i, για τους οποίους εκτελείται αυτή η κατάσταση, υποδηλώνουμε το E0 ,. Εάν το E0 αποτελείται από ένα στοιχείο, τότε η βάση των συνθηκών ΑΙ αποκλείεται από τη βάση (η μεταβλητή XI γίνεται μη μπέικον). Εάν το E0 αποτελείται από περισσότερα από ένα στοιχεία, το σύνολο E1 καταρτίζεται, το οποίο αποτελείται από τα οποία επιτυγχάνεται. Εάν το Ε1 αποτελείται από έναν δείκτη Κ, η μεταβλητή XK εμφανίζεται από τη βάση. Διαφορετικά, πολλά Ε2 καταρτίζονται, κλπ. Πρακτικά, είναι απαραίτητο να χρησιμοποιηθεί εάν έχει ήδη ανακαλυφθεί η βρόχο.

Εναλλακτική λύση στο βέλτιστο σε ZLP ?????????????????

60. Η μέθοδος τεχνητής βάσης. M-εργασία. Το θεωρητικό σύνδεσης μεταξύ των λύσεων του αρχικού προβλήματος και της εργασίας M.

Μέθοδος τεχνητής βάσης.

Η μέθοδος τεχνητής βάσης χρησιμοποιείται για να βρει την επιτρεπόμενη βασική λύση του γραμμικού προβλήματος προγραμματισμού, όταν υπάρχουν οι συνθήκες του τύπου των εξισώσεων στην κατάσταση. Εξετάστε την εργασία:

max (f (x) \u003d ccixi | sajixi \u003d bj, j \u003d 1, m; xi≥0).

Σε περιορισμούς, οι λεγόμενες "τεχνητικές μεταβλητές" RJ ως εξής:

Atejix + rj \u003d bj, j \u003d 1, m, f (x) \u003d ccixi-msrj

Με την εισαγωγή τεχνητών μεταβλητών στη μέθοδο τεχνητής βάσης, ένας επαρκώς μεγάλος συντελεστής M αποδίδεται στη λειτουργία στόχου, η οποία έχει νόημα του προστίμου για την εισαγωγή τεχνητών μεταβλητών. Σε περίπτωση ελαχιστοποίησης, οι τεχνητές μεταβλητές προστίθενται στη λειτουργία στόχου με τον συντελεστή M. Η εισαγωγή τεχνητών μεταβλητών επιτρέπεται εάν κατά τη διάρκεια του προβλήματος της επίλυσης του προβλήματος αναφέρεται με συνέπεια στο μηδέν.

Ο πίνακας Simplex, ο οποίος καταρτίζεται στη διαδικασία διαλύματος χρησιμοποιώντας τη μέθοδο τεχνητής βάσης, καλείται εκτεταμένη. Διαφέρει από το συνηθισμένο στο ότι περιέχει δύο σειρές για τη λειτουργία του στόχου: ένα - για το στοιχείο F \u003d scixi και το άλλο είναι για το στοιχείο M SRJ, θεωρούμε τη διαδικασία επίλυσης του προβλήματος σε ένα συγκεκριμένο παράδειγμα.

Παράδειγμα 1. Βρείτε τη μέγιστη λειτουργία F (x) \u003d -x1 + 2x2 - x3 με περιορισμούς:

x1≥0, x2≥0, x3≥0.

Εφαρμόστε τη μέθοδο τεχνητής βάσης. Εισάγουμε τεχνητές μεταβλητές στους περιορισμούς του προβλήματος

2x1 + 3x2 + x3 + R1 \u003d 3;

x1 + 3x3 + r2 \u003d 2;

Η λειτουργία του σκοπού f (x) -m σRJ \u003d -x1 + 2x2- x3- m (R1 + R2).

Εκφράστε το άθροισμα R1 + R2 από το σύστημα ορίου: R1 + R2 \u003d 5 - 3x1 - 3x2-4x3, κατόπιν f (x) \u003d -x1 + 2x2- x3 - m (5 - 3x1 - 3x2-4x3).

Κατά την κατάρτιση του πρώτου πίνακα απλού απλού (Πίνακας 1), υποθέτουμε ότι οι αρχικές μεταβλητές X1, X2, X3 δεν αποσυνδέονται, και οι εισαγόμενες τεχνητές μεταβλητές είναι βασικές. Στα καθήκοντα μεγιστοποίησης, το σημάδι των συντελεστών με μεταβλητές μη μπέικον στις γραμμές F- και M αλλά αλλαγές στο αντίθετο. Το σήμα συνεχούς τιμής στη συμβολοσειρά M δεν αλλάζει. Η βελτιστοποίηση εκτελείται πρώτα από τη γραμμή M. Επιλογή της στήλης και των γραμμών του ξενιστή, όλοι οι μετασχηματισμοί απλών αποβλήτων στην πρόοδο της μεθόδου τεχνητής βάσης πραγματοποιούνται όπως στη συνήθη μέθοδο απλού.

Η μέγιστη αξία χωρίς αποκλεισμούς του αρνητικού συντελεστή (-4) καθορίζει τη στήλη μολύβδου και τη μεταβλητή X3, η οποία θα μεταβεί στη βάση. Επομένως, ο ελάχιστος λόγος απλού απλού συστήματος (2/3) αντιστοιχεί στη δεύτερη γραμμή του πίνακα, η μεταβλητή R2 πρέπει να εξαιρεθεί από τη βάση. Το στοιχείο μολύβδου κυκλώνεται με το περίγραμμα.

Στην τεχνητή βάση, οι τεχνητές μεταβλητές, που εξαιρούνται από τη βάση, δεν επιστρέφονται πλέον σε αυτό, επομένως οι στήλες των στοιχείων τέτοιων μεταβλητών μειώνεται. Τραπέζι. 2. Μειωμένη σε 1 στήλη. Με εκ νέου υπολογισμό αυτού του πίνακα, πηγαίνετε στο τραπέζι. 3. Στο οποίο επαναφέρεται η γραμμή M, μπορεί να αφαιρεθεί. Μετά τον αποκλεισμό από τη βάση όλων των τεχνητών μεταβλητών, λαμβάνουμε μια επιτρεπόμενη βασική λύση του αρχικού προβλήματος, το οποίο στο παράδειγμα που εξετάζεται είναι βέλτιστο:

x1 \u003d 0; x2 \u003d 7/9; Fmax \u003d 8/9.

Εάν, κατά την αφαίρεση της γραμμής M, το διάλυμα δεν είναι βέλτιστο, τότε η διαδικασία βελτιστοποίησης συνεχίζεται και εκτελείται με τη συνήθη μέθοδο απλού. Εξετάστε ένα παράδειγμα στο οποίο υπάρχουν περιορισμοί όλων των τύπων: ≤, \u003d, ≥

Το έργο

Βρείτε τα βέλτιστα μεγέθη της παραγωγής ειδών Α, Β και Β. Κόστος πρώτων υλών ανά μονάδα παραγωγής: Α - 5, Β - 2, Β - 4. Ο όγκος των πρώτων υλών είναι 2000 μονάδες. Κόστος εξοπλισμού ανά μονάδα παραγωγής: A - 4, B - 5, B - 4. Ο όγκος του εξοπλισμού είναι 1000 μονάδες. Κέρδος από την πώληση μιας μονάδας προϊόντων: Α - 10, Β - 8, στο 12. Το κριτήριο - το μέγιστο κέρδος της επιχείρησης. Η παραγωγή προϊόντων Α πρέπει να είναι τουλάχιστον 100 μονάδες. Η παραγωγή προϊόντων Β πρέπει να είναι τουλάχιστον 50 μονάδες.

Λύση του προβλήματος της μεθόδου simplex m

1) Προσδιορισμός του βέλτιστου σχεδίου παραγωγής

Ας x1, x2, x3 να είναι η ποσότητα των προϊόντων που παράγονται από τη μορφή Α, Β, Β, αντίστοιχα. Στη συνέχεια το μαθηματικό μοντέλο του προβλήματος είναι:

F \u003d 10 · x1 + 8 · x2 + 12 · x3 -\u003e max

Εισάγουμε πρόσθετες μεταβλητές x4 ≥ 0, x5 ≥ 0, x6 ≥ 0, x7 ≥ 0 έτσι ώστε οι ανισότητες να μετατρέπονται σε ισοτιμίες.

Για να επιλέξετε μια αρχική βάση, εισάγουμε τεχνητές μεταβλητές x8 ≥ 0, x9 ≥ 0 και πολύ μεγάλο αριθμό m (m -\u003e ∞). Επιλύουμε τη μέθοδο M.

F \u003d 10 · x1 + 8 · x2 + 12 · x3 + 0 · x4 + 0 · x5 + 0 · x6 + 0 · x7- m · x8- m · x9 -\u003e max

Ως βάση, πάρτε x4 \u003d 2000. x5 \u003d 1000; x8 \u003d 100; x9 \u003d 50.

Δεδομένα Εισάγετε τον πίνακα Simplex

Simplex πίνακα αρ. 1

Χαρακτηριστικό στόχου:

0 · 2000 + 0 · 1000 + (- m) · 100 + (- m) · 50 \u003d - 150m

Υπολογίστε τις εκτιμήσεις του τύπου:

Δ1 \u003d 0 · 5 + 0 · 4 + (- Μ) · 1 + (- Μ) · 0-10 \u003d - Μ - 10

Δ2 \u003d 0 · 2 + 0 · 5 + (- m) · 0 + (- m) · 1 - 8 \u003d - m - 8

Δ3 \u003d 0 · 4 + 0 · 4 + (- m) · 0 + (- m) · 0 - 12 \u003d - 12

Δ4 \u003d 0 · 1 + 0 · 0 + (- m) · 0 + (- m) · 0 - 0 \u003d 0

Δ5 \u003d 0 · 0 + 0 · 1 + (- m) · 0 + (- m) · 0 - 0 \u003d 0

Δ6 \u003d 0 · 0 + 0 · 0 + (- m) · (-1) + (- m) · 0 - 0 \u003d m

Δ7 \u003d 0 · 0 + 0 · 0 + (- m) · 0 + (- m) · (-1) - 0 \u003d m

Δ2 \u003d 0 · 0 + 12 · 0 + 10 · 0 + 8 · 1 - 8 \u003d 0

Δ3 \u003d 0 · 0 + 12 · 1 + 10 · 0 + 8 · 0 - 12 \u003d 0

Δ4 \u003d 0 · 1 + 12 · 0 + 10 · 0 + 8 · 0 - 0 \u003d 0

Δ5 \u003d 0 · (-1) + 12 · 1/4 + 10 · 0 + 8 · 0 - 0 \u003d 3

Δ6 \u003d 0 · 1 + 12 · 1 + 10 · (-1) + 8 · 0 - 0 \u003d 2

Δ7 \u003d 0 · (-3) + 12 · 5/4 + 10 · 0 + 8 · (-1) - 0 \u003d 7

Δεδομένου ότι δεν υπάρχουν αρνητικές εκτιμήσεις, το σχέδιο είναι βέλτιστο.

Επίλυση του προβλήματος: x1 \u003d 100; x2 \u003d 50; x3 \u003d 175/2 \u003d 87.5; x4 \u003d 1050; x5 \u003d 0; x6 \u003d 0; x7 \u003d 0; Fmax \u003d 2450.

Απάντηση: x1 \u003d 100; x2 \u003d 50; x3 \u003d 175/2 \u003d 87.5; x4 \u003d 1050; x5 \u003d 0; x6 \u003d 0; x7 \u003d 0; Fmax \u003d 2450Ο Είναι απαραίτητο να παραχθούν x1 \u003d 100 μονάδες προϊόντων της μορφής Α, Χ2 \u003d 50 μονάδες του προϊόντος της μορφής Β και Χ3 \u003d 87,5 μονάδες προϊόντων του τύπου V. Το μέγιστο κέρδος θα είναι Fmax \u003d 2450 μονάδες .

Το θεωρητικό σύνδεσης μεταξύ των λύσεων του αρχικού προβλήματος και της εργασίας M.

???????????????????????

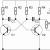
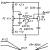
Σκεφτείτε λεπτομερώς πώς οι πίνακες Simplex υπολογίζονται εκ νέου (στο παράδειγμα μιας επανάληψης). Ας υποθέσουμε ότι υπάρχει ένας απλός πίνακας που αντιπροσωπεύεται Εικ.. Το έργο της μεγιστοποίησης της λειτουργίας στόχου επιλύεται. Η στήλη επιτόπου αντιστοιχεί στη μεταβλητή x 2και να επιλύσετε μια μεταβλητή συμβολοσειρά x 3. (Κόκκινοι αριθμοί), στην τομή τους υπάρχει ένα στοιχείο ανάλυσης (κύτταρο με γκρίζο φόντο). Το πρώτο πράγμα που πρέπει να κάνουμε είναι να το αντικαταστήσουμε. Η επιδιόρθωση της συμβολοσειράς δείχνει ποια μεταβλητή πρέπει να αφαιρεθεί από τη βάση (στην περίπτωσή μας x 3.) και η επιτρεπτική στήλη δείχνει ποια μεταβλητή θα πρέπει να εισάγει τη βάση (στην περίπτωσή μας x 2). Στο Εικ. 2 Το γεγονός αντικατάστασης επικεντρώνεται στην μπλε γραμμή.

Τώρα επανολογούμε τα στοιχεία που στέκονται στη σειρά ανάλυσης. Για να το κάνετε αυτό, απλά διαιρέστε το καθένα από αυτά στο στοιχείο ανάλυσης (στο παράδειγμά μας 4 ). Και όλα τα στοιχεία της επαναφοράς της στήλης ανάλυσης, εκτός από το στοιχείο που στέκεται στη σειρά ανάλυσης. (Βλέπω Εικ. 2)

Εικόνα 1

Τα υπόλοιπα επιτραπέζια κύτταρα (εκτός από τη στήλη "στάσης") υπολογίζονται εκ νέου από το λεγόμενο Κανόνας ορθογωνίου, η έννοια του οποίου είναι ευκολότερη να κατανοήσουμε το παράδειγμα. Αφήστε να χρειαστεί να υπολογίσετε ξανά το στοιχείο που περιβάλλεται Εικ. Κόκκινο περίγραμμα. Περνάμε διανοητικά από αυτό μια κάθετη και οριζόντια γραμμή στη διασταύρωση, με μια στήλη ανάλυσης και επίλυση στήλης. Στοιχεία που στέκονται στις θέσεις διέλευσης που κυκλώνονται με μπλε περιγράμματα (βλ Εικ.). Η νέα τιμή του στοιχείου "κόκκινου" θα είναι η τρέχουσα τιμή του στοιχείου του μείον του προϊόντος του "μπλε" διαιρούμενο στο στοιχείο που επιτρέπει ("γκρι") (βλ. Εικ.). Δίνω: 18 - (64 * -1) / 4 = 34 , εδώ είναι ένα σημάδι " * "Εμφανίζεται η λειτουργία πολλαπλασιασμού.
Γράψτε νέα σημασία στην προηγούμενη θέση σας (βλ Εικ. 2 Κόκκινο περίγραμμα).

Σχήμα 2.

Χρησιμοποιώντας αυτόν τον κανόνα, συμπληρώστε όλα τα κενά στοιχεία του πίνακα (εκτός από τη στήλη "Στάση") Εικ. 3.. Μετά από αυτό, ορίζουμε μια νέα στήλη που επιτρέπει. Για να το κάνετε αυτό, αναλύστε τη συμβολοσειρά "Q" Και δεδομένου ότι το καθήκον μας είναι το μέγιστο, θα το βρούμε σε αυτό Μέγιστο θετικό στοιχείο, Θα καθορίσει τη στήλη. Στην περίπτωσή μας, αυτό 3/2 . Όλα τα στοιχεία της στήλης ανάλυσης εμφανίζονται σε μια κόκκινη γραμματοσειρά (βλ Εικ. 3.). Αν μετά την επόμενη επανάληψη στη συμβολοσειρά "Q" Δεν θα είναι θετικά στοιχεία - αυτό σημαίνει ότι επιτυγχάνεται η βέλτιστη λύση, οι επαναλήψεις τερματίζονται. Εάν η εργασία μας ήταν ελάχιστη, τότε η επιτρεπτική στήλη θα προσδιοριστεί από το ελάχιστο αρνητικό στοιχείο και αν μετά την επόμενη επανάληψη στη συμβολοσειρά "Q" Τα αρνητικά στοιχεία δεν θα είναι, αυτό σημαίνει ότι επιτυγχάνεται η βέλτιστη λύση.

Σχήμα 3.

Τώρα γεμίστε τη στήλη "στάση". Για να το κάνετε αυτό, χρειάζεστε το αντίστοιχο (στέκεται στην ίδια γραμμή) το στοιχείο στήλης "διάλυμα" διαιρείται σε ένα κατάλληλο στοιχείο της στήλης ανάλυσης (βλ Εικ. 3.). Σημείωσηότι η λειτουργία αυτή πραγματοποιείται Μόνο για θετική Επιτρεπόμενα στοιχεία στήλης και συμβολοσειρά "Q" Αυτή η λειτουργία δεν συμμετέχει σε αυτή τη λειτουργία. Εάν μετά από κάποια επανάληψη στη στήλη ανάλυσης δεν θα είναι θετικά στοιχεία, τότε αυτή η εργασία είναι αδιάλυτη λόγω της απεριόριστης λειτουργίας στόχου, οι επαναλήψεις τερματίζονται.

Μετά την πλήρωση της στήλης "αναλογίας", ορίζουμε μια νέα συμβολοσειρά. Προσδιορίζεται από το ελάχιστο στοιχείο από τη στήλη "στάσης". Στην περίπτωσή μας, αυτό 32 Όλα τα στοιχεία της επιτόπισης της συμβολοσειράς εμφανίζονται με κόκκινο χρώμα (βλ Εικ. 3.). Αυτό, η επόμενη επανάληψη τελειώνει, η ακόλουθη μεταβλητή επανάληψης x 2 θα αποσυρθεί από τη βάση (αυτό μας λέει μια νέα επιτόπια συμβολοσειρά), η θέση του θα πάρει μια μεταβλητή x 1 (Μιλάμε για αυτή τη νέα στήλη που επιτρέπουν) και όλοι οι υπολογισμοί θα επαναλάβουν ξανά.

Η παραπάνω μετατροπή εκτελείται εύκολα σε ειδικούς πίνακες που ονομάζονται πίνακες απλού.

Τα ακόλουθα μπλοκ κατανέμονται στον πίνακα Simplex:

Γράφουμε τη λύση του παραδείγματος ενός παραδείγματος από το τμήμα 3.3 στους πίνακες Simplex:

Όλα τα δεδομένα πηγής που περιέχονται στη μαθηματική κατάσταση της εργασίας μεταφέρονται στον πρώτο πίνακα απλού. Bore δωρεάν μεταβλητές, λάβετε ένα σχέδιο αναφοράς

Στην τελευταία σειρά του πρώτου πίνακα Simplex, εισάγουμε το κριτήριο σε σιωπηρή μορφή

Αποκλείουμε από αυτό το κριτήριο μια βασική μεταβλητή x 4, οδηγώντας ένα κριτήριο στο μυαλό

Για λύσεις βελτιστοποίησης, όλες οι εκτιμήσεις πρέπει να είναι μη αρνητικές

Η απόφαση δεν είναι βέλτιστη, διότι Υπάρχουν αρνητικές εκτιμήσεις.

Οι εκτιμήσεις μπορούν να υπολογιστούν από τους τύπους. Το προϊόν είναι ο τρέχων φορέας της μήτρας των συνθηκών, τότε η εκτίμηση της ελεύθερης μεταβλητής μπορεί να υπολογιστεί ως κλιμακωτό προϊόν του φορέα των συντελεστών με βασικές μεταβλητές στον τρέχοντα φορέα της μήτρας των συνθηκών μείον τον συντελεστή λειτουργίας στόχου με τον συντελεστή Αυτή η μεταβλητή. Έτσι, για να πάρει την αξία

Η στήλη ανάλυσης επιλέγεται από αυτή όπου η μικρότερη εκτίμηση (εάν η εργασία είναι μέγιστη). Και για να επιλέξετε τη γραμμή ανάλυσης, είναι απαραίτητο να βρείτε μεταξύ όλων των γραμμών, εκφραζόμενες από τις οποίες μεταβλητή, μείωση, η οποία μετατρέπεται σε μηχάνημα γρηγορότερα.

Ως αποτέλεσμα, λαμβάνουμε ότι η στήλη ανάλυσης είναι και η συμβολοσειράς ανάλυσης είναι. Έτσι, από τη λίστα βασικών, αποδεικνύεται η μεταβλητή και εισέρχεται στη μεταβλητή.

Η απόφαση δεν είναι βέλτιστη, διότι Υπάρχει αρνητική βαθμολογία -2.

Η λύση είναι βέλτιστη, επειδή Όλες οι εκτιμήσεις είναι περισσότερο μηδέν. Προφανώς, είναι αδύνατο να αυξηθεί.

Κανόνες για τα τραπέζια simplex

Ο πίνακας Simplex είναι κατασκευασμένος για οποιαδήποτε λύση αναφοράς.

Αφήστε τη λύση αναφοράς. Ο πίνακας απλού μέσου για αυτή τη λύση έχει τη μορφή

Βάση Matrix B \u003d (A 1, A 2, ... A M)

· Για βασικές μεταβλητές, η τρέχουσα μήτρα είναι ενιαία.

• · Οποιαδήποτε στήλη.
• · Vector σωστά μέρη περιορισμών.
• · Οι εκτιμήσεις για τις ελεύθερες μεταβλητές δεν είναι μηδέν

· Στο δεξιό κύτταρο - η αξία του κριτηρίου

Στάδια της λειτουργίας απλού

• 1. Ελέγξτε για βελτιστοποίηση ()
• 2. Εάν υπάρχει, η λύση δεν είναι βέλτιστη. Στη συνέχεια, επιλέξτε μια στήλη με μια ελάχιστη αξιολόγηση. Θα το επιτρέπει.
• 3. Η γραμμή ανάλυσης επιλέγεται στην ελάχιστη αναλογία ελεύθερων μελών σε θετικούς διαλυτούς συντελεστές στήλης. Η βασική μεταβλητή που εκφράζεται από αυτή τη σειρά εξέρχεται από τη λίστα των βασικών μεταβλητών. Εκείνοι. X k φύλλα, αλλά το X S εισέρχεται.

• 4. Ο τρέχων πίνακας Simplex μετατρέπεται στον ακόλουθο κανόνα:
  • · Η συμβολοσειρά ανάλυσης χωρίζεται στο στοιχείο που επιτρέπει:

• · Η επίλυση της στήλης αντικαθίσταται από ένα μόνο.
• · Όλα τα άλλα στοιχεία του πίνακα Simplex μπορούν να υπολογιστούν εκ νέου σύμφωνα με τον κανόνα του τετράκλιου:

Το τετράκλινο στο διαγώνιο που συνδέει το επιθυμητό στοιχείο είναι διανοητικά χτισμένο. Στη συνέχεια, η τιμή νέου στοιχείου ισούται με το ίδιο μείον το προϊόν των στοιχείων στην αντίθετη διαγώνια χωρίζεται στο στοιχείο.

Ή η νέα τιμή του στοιχείου είναι ίση με το προϊόν των αντικειμένων στην κύρια διαγώνιο μείον το προϊόν των στοιχείων στην αντίθετη διαγώνια και όλα αυτά διαιρούμενα στο στοιχείο.

Σχόλιο : Εάν υπήρχε μηδενικό στοιχείο στη γραμμή ανάλυσης, τότε αυτή η στήλη δεν αλλάζει. Εάν υπάρχει μηδενικό στοιχείο στη στήλη ανάλυσης, τότε η αντίστοιχη γραμμή δεν αλλάζει.

Η μέθοδος Gauss-Jordan έχει σχεδιαστεί για να λύσει συστήματα γραμμικών αλγεβρικών εξισώσεων (Slava). Είναι μια τροποποίηση της μεθόδου Gauss. Εάν η μέθοδος Gauss πραγματοποιηθεί σε δύο στάδια (άμεση διαδρομή και αντίστροφα), τότε η μέθοδος Gauss-Jordan σάς επιτρέπει να λύσετε το σύστημα σε ένα βήμα. Λεπτομέρειες και άμεσο σύστημα εφαρμογής της μεθόδου Gauss-Jordan περιγράφονται στα παραδείγματα.

Σε όλα τα παραδείγματα $ a $ δηλώνει το σύστημα Matrix, $ \\ Widetilde (A) $ είναι μια εκτεταμένη μήτρα συστήματος. Μπορείτε να διαβάσετε σχετικά με τη μορφή Matrix της γραφής μιας λέξης.

Παράδειγμα №1

Επίλυση $ \\ Αριστερά \\ (\\ Ξεκινήστε (ευθυγραμμισμένο) & 4x_1-7x_2 + 8x_3 \u003d -23; \\\\ & 2x_1-4x_2 + 5x_3 \u003d -13; \\\\ /--3x_1 + 11x_2 + x_3 \u003d 16. \\ END (ευθυγραμμισμένο) \\ Δεξιά. Μέθοδος Gaussa-Jordan.

Ας προχωρήσουμε από την τελευταία μήτρα που λάβαμε στο σύστημα:

$$ \\ Αριστερά \\ (\\ Ξεκινήστε (ευθυγραμμισμένο) & 0 \\ CDOT X_2 + 0 \\ CDOT X_3 \u003d 1; \\\\ & 1 \\ CDOT X_1 + 0 \\ CDOT X_2 + 0 \\ CDOT X_3 \u003d -2; \\\\ & 0 \\ CDOT X_1 + 0 \\ CDOT X_2 + 1 \\ CDOT X_3 \u003d -1. \\ END (ευθυγραμμισμένο) \\ Δεξιά. $$$

Απλούστευση του συστήματος που προκύπτει, έχουμε:

$$ \\ Αριστερά \\ (\\ Ξεκινήστε (ευθυγραμμισμένο) & x_2 \u003d 1; \\\\ & x_1 \u003d -2; \\\\ & x_3 \u003d -1. \\ end (ευθυγραμμισμένο) \\ Δεξιά. $$

Η πλήρης λύση χωρίς εξηγήσεις μοιάζει με αυτό:

Τουλάχιστον αυτή η μέθοδος επιλογής των στοιχείων ανάλυσης είναι αρκετά παραδεκτή, αλλά κατά προτίμηση επιλέξτε τα διαγώνια στοιχεία της μήτρας συστήματος ως στοιχεία ανάλυσης. Θα εξετάσουμε αυτή τη μέθοδο παρακάτω.

Η επιλογή των στοιχείων επίλυσης στην κύρια διαγώνια της μήτρας συστήματος.

Δεδομένου ότι αυτή η λύση είναι εντελώς παρόμοια με την προηγούμενη (εκτός από την επιλογή των στοιχείων ανάλυσης), τότε ας χάσουμε τις λεπτομερείς εξηγήσεις. Η αρχή της επιλογής των στοιχείων ανάλυσης είναι απλή: Στην πρώτη στήλη, επιλέξτε το στοιχείο της πρώτης γραμμής, στη δεύτερη στήλη λαμβάνουμε το στοιχείο της δεύτερης γραμμής, στην τρίτη στήλη - το στοιχείο της τρίτης γραμμής και ούτω καθεξής.

Το πρώτο βήμα

Στην πρώτη στήλη, επιλέξτε το πρώτο στοιχείο συμβολοσειράς, δηλ. Ως ψήφισμα, έχω ένα στοιχείο 4. Κατανοώ ότι η επιλογή του αριθμού 2 φαίνεται πιο προτιμότερη, δεδομένου ότι ο αριθμός αυτός είναι ακόμα μικρότερος από 4. Για να μετακινηθείτε στον πρώτο σημείο, αλλάζουμε Η πρώτη και η δεύτερη γραμμή για να αλλάξετε την πρώτη και τη δεύτερη γραμμή:

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCC | C) 4 & -7 & 8 & 23 \\\\ 2 & -4 & -13 \\ el (ARTAR) \\ Δεξιά) \\ Δεξιά (ARRAY) (CCC | C) 2 & -4 & 5 & 6 & 13 \\\\ 4 & -7 & 8 & -23 \\ END & 11 & 1 & 16 \\ END (ARTAY) \\ RWORE) $$

Έτσι, το στοιχείο που επιθυμεί αντιπροσωπεύεται από τον αριθμό 2. Με τον ίδιο τρόπο, όπως και πριν, διαιρούμε την πρώτη γραμμή κατά 2 και στη συνέχεια να επαναφέρετε τα στοιχεία της πρώτης στήλης:

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCC | C) 2 & -4 & 5 & 14 \\\\ 4 & -7 & 8 & 23 \\ End & 11 & 1 & 16 \\ END (ARTAY) \\ ) \\ Begin (Array) (L) I: 2 \\ Phantom (0) \\ \\ \\ \\ \\ Phantom (0) \\ END (ARTAY) \\ Δεξιάλαξη \\ αριστερά (\\ Έναρξη (Array) (CCC | C) 1 & - 2 & 5/2 & -13/2 \\\\ 4 & -7 & 11 & 1 & 1 & 1 & 1 & 16 \\ END (ARTAR) \\ Δεξιά) \\ Ξεκινήστε (Array) (L) \\ Phantom (0) \\\\ II-4 \\ CDOT I \\\\ III + 3 \\ CDOT I \\ END (ARRAY) \\ ROSTROW \\ Αριστερά (\\ Έναρξη (Array) (CCC | C) 1 & -2 & 5/2 & -2 & -2 & 3 \\\\ 0 & 5 & 17/2 & -7/2 \\ END (ARTAY) \\ Δεξιά). $$.

Δεύτερο βήμα

Στο δεύτερο βήμα, είναι απαραίτητο να επαναφέρετε τα στοιχεία της δεύτερης στήλης. Στην ποιότητα του στοιχείου ανάλυσης, επιλέξτε το στοιχείο της δεύτερης γραμμής, δηλ. 1. Το επιτρεπτό στοιχείο είναι ήδη ίσο με ένα, οπότε δεν θα αλλάξουμε γραμμές. Με την ευκαιρία, αν θέλαμε να αλλάξουμε τις γραμμές σε μέρη, η πρώτη γραμμή δεν θα άγγιξε, καθώς χρησιμοποιήθηκε ήδη στο πρώτο βήμα. Αλλά η δεύτερη και η τρίτη γραμμή μπορούν εύκολα να αλλάξουν σε μέρη. Ωστόσο, επαναλαμβάνω, σε αυτή την περίπτωση, δεν είναι απαραίτητο να αλλάξετε τη συμβολοσειρά σε ορισμένες θέσεις, επειδή το επιτρεπτικό στοιχείο είναι ήδη βέλτιστο - είναι ίσο με ένα.

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCC | C) 1 & -2 & 5/2 & -1/2 \\\\ 0 & 1 & -2 & 3 \\\\ 0 & -7 / 2 \\ τέλος (πίνακας) \\ Δεξιά) \\ Ξεκινήστε (Array) (L) I + 2 \\ CDOT II \\ \\ PHANTOM (0) \\\\ III-5 \\ CDOT II \\ END (ARTAY) \\ Δεξιά Ξεκινήστε (CCC) (CCC | C) 1 & 0 & -3/2 & -1/2 \\\\ 0 & 1 & 2 & 3 \\\\ 0 & 0 & 37/2 & 37/2 \\ END (ARTAR) \\ Σωστά). $$.

Το δεύτερο βήμα έχει τελειώσει. Πηγαίνετε στο τρίτο βήμα.

Τρίτο βήμα

Στο τρίτο βήμα, απαιτείται να επαναφέρετε τα στοιχεία της τρίτης στήλης. Στην ποιότητα του στοιχείου ανάλυσης, επιλέξτε το στοιχείο της τρίτης γραμμής, δηλ. 37/2. Διαιρούμε τα στοιχεία της τρίτης γραμμής κατά 37/2 (έτσι ώστε το στοιχείο ανάλυσης να γίνει 1) και στη συνέχεια να επαναφέρετε τα αντίστοιχα στοιχεία της τρίτης στήλης:

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCC | C) 1 & 0 & -3/2 & -1/2 \\\\ 0 & 1 & 2 & 3 \\\\ 0 & 0 & 377 / 2 \\ τέλος (συστοιχία) \\ Δεξιά) \\ Ξεκινήστε (Array) (L) \\ Phantom (0) \\\\ \\ Phantom (0) \\\\ III: \\ Frac (37) (2) \\ End (Array) \\ αριστερά (\\ begin (Array) (ΚΤΚ | C) 1 & 0 & -3/2 -1/2 & \\\\ 0 & 1 & -2 & 3 \\ ΕΔ (Array) \\ δεξιά) \\ Αρχίστε (Array) (L ) I + 2 \\ cdot III \\\\ II + 3/2 \\ cdot III \\\\ \\ PHANTOM (0) \\ END (Array) \\ Rightarrow \\ αριστερά (\\ begin (Array) (ΚΤΚ | C) 1 & 0 & 0 & 1 \\\\ 0 & 0 & 1 & 1 \\ END (ARTAY) \\ Δεξιά). $$.

Η απάντηση αποκτάται: $ x_1 \u003d -2 $, $ x_2 \u003d 1 $, $ x_3 \u003d -1 $. Η πλήρης λύση χωρίς εξηγήσεις μοιάζει με αυτό:

Όλα τα άλλα παραδείγματα σε αυτή τη σελίδα θα λυθούν με τη δεύτερη θέση: ως ψήφισμα, θα επιλέξουμε τα διαγώνια στοιχεία της μήτρας συστήματος.

Απάντηση: $ x_1 \u003d -2 $, $ x_2 \u003d 1 $, $ x_3 \u003d -1 $.

Παράδειγμα αριθ. 2.

Λύστε $ \\ αριστερό \\ (\\ begin (ευθυγραμμισμένες) και 3x_1 + x_2 + 2x_3 + 5x_4 \u003d -6? \\\\ & 3x_1 + x_2 + 2x_4 \u003d -10? \\\\ & 6x_1 + 4x_2 + 11x_3 + 11x_4 \u003d -27? \\ \\ & -3x_1-2x_2-2x_3-10x_4 \u003d 1. \\ end (ευθυγραμμισμένο) \\ Δεξιά. $ Gaussa-jordan μέθοδος.

Γράφουμε ένα εκτεταμένο μήτρα αυτού του συστήματος: $ \\ Widetilde (A) \u003d \\ Αριστερά (\\ Ξεκινήστε (Array) (CCCC | C) 3 & 1 & 2 & 5 & 0 & 2 & - 10 \\\\ 6 & 4 & 11 & 11 & -27 \\\\ -3 & -2 & -2 & -10 & 1 \\ END (Array) \\ Δεξιά) $.

Στην ποιότητα των στοιχείων ανάλυσης, θα επιλέξετε τα διαγώνια στοιχεία της μήτρας συστήματος: Στο πρώτο βήμα, παίρνουμε το στοιχείο της πρώτης χορδής, στο δεύτερο βήμα, το στοιχείο της δεύτερης γραμμής και ούτω καθεξής.

Το πρώτο βήμα

Πρέπει να επαναφέρουμε τα αντίστοιχα στοιχεία της πρώτης στήλης. Ως στοιχείο ανάλυσης, πάρτε ένα στοιχείο της πρώτης γραμμής, δηλ. 3. Κατά συνέπεια, η πρώτη γραμμή θα πρέπει να χωριστεί σε 3 έτσι ώστε το στοιχείο ανάλυσης να είναι ίσο με ένα. Και στη συνέχεια να επαναφέρετε όλα τα στοιχεία της πρώτης στήλης, εκτός από την ανάλυση:

$$ \\ αριστερά (\\ begin (array) (CCCC | C) 3 & 1 & 2 & 5 & -6 \\\\ 3 & 1 & 0 & 2 & 11 & -27 & 4 & 11 & 11 & -27 \\ \\ 3 & -2 & -2 & -10 & 1 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) Ι: 3 \\\\ \\ PHANTOM (0) \\\\\\ Phantom (0) \\\\\\ Φάντασμα ( 0) \\ end (Array) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 1/3 & 2/3 & 5/3 & 2 & 2 & 2 & 2 & 2 & -10 \\\\ 6 & 4 & 11 & 11 & -27 \\\\ -3 & -2 & -2 & -10 & 1 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) \\ PHANTOM (0) \\\\ II- 3 \\ cdot Ι \\\\ ΙΙΙ-6 \\ cdot Ι \\\\ IV + 3 \\ cdot Ι \\ END (Array) \\ Rightarrow \\\\\\\\\\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 1 / 3 & 2/3 & 5/3 & -2 \\\\ 0 & 0 & -2 & -3 & 7 & -15 \\\\ 0 & -1 & 0 & - 5 & -5 \\ END (Array) \\ Σωστά). $$.

Δεύτερο βήμα

Πηγαίνετε στο μηδενισμό των αντίστοιχων στοιχείων της δεύτερης στήλης. Στην ποιότητα του στοιχείου ψηφίσματος, είχαμε ανέβηκε για να λάβει το στοιχείο της δεύτερης γραμμής, αλλά εμείς δεν το κάνουμε αυτό, δεδομένου ότι το επιθυμητό στοιχείο είναι μηδενική. Συμπέρασμα: Θα αλλάξουμε τις γραμμές σε μέρη. Είναι αδύνατο να αγγίξετε την πρώτη συμβολοσειρά, καθώς έχει ήδη χρησιμοποιηθεί στο πρώτο βήμα. Η επιλογή δεν είναι υψηλή: ή αλλάζουμε τη δεύτερη και την τρίτη γραμμή σε ορισμένα μέρη, ή αλλάζουμε το τέταρτο και το δεύτερο και το δεύτερο. Δεδομένου ότι στην τέταρτη γραμμή χύνεται (-1), τότε ακόμη και η τέταρτη γραμμή στην "ανταλλαγή". Έτσι, αλλάζουμε σε μέρη τη δεύτερη και την τέταρτη γραμμή:

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCCC | C) 1 & 1/3 & 2/3 & 5/3 & -2 \\\\ 0 & 0 & 0 & 2 & 4 \\\\ 0 & 2 & 7 & 1 & -15 \\\\ 0 & -1 & 0 & -5 & -5 \\ END (Array) \\ Δεξιά) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 1/3 & 2/3 & 5/3 & -2 \\\\ 0 & -1 & 0 & -5 & -5 \\\\ 0 & 2 & 7 & 1 & -15 \\\\ 0 & 0 & -2 & -3 & -4 \\ End (Array) \\ Δεξιά) $$

Τώρα όλα είναι φυσιολογικά: το στοιχείο ανάλυσης ισούται με (-1). Συμβαίνει, παρεμπιπτόντως, ότι οι αλλαγές των γραμμών δεν είναι δυνατές, αλλά θα συζητήσουν στο ακόλουθο παράδειγμα αριθ. 3. Εν τω μεταξύ, διαιρούμε τη δεύτερη συμβολοσειρά στο (-1) και στη συνέχεια επαναφέρετε τα στοιχεία της δεύτερης στήλης. Παρακαλείστε να σημειώσετε ότι στη δεύτερη στήλη το στοιχείο που βρίσκεται στην τέταρτη γραμμή είναι ήδη μηδέν, οπότε δεν θα αγγίξουμε την τέταρτη γραμμή.

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCCC | C) 1 & 1/3 & 2/3 & 5/3 & -2 \\\\ 0 & -1 & 0 & 2 & 7 & 1 & -15 \\\\ 0 & 0 & -2 & -3 & -4 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) \\ PHANTOM (0) \\\\ II: (- 1) \\\\\\ Phantom (0) \\\\\\ Phantom (0) \\ End (Array) \\ Δεξιά \\ Αριστερά (\\ Έναρξη (Array) (CCCC | C) 1 & 1/3 & 2/3 & 5/3 & -2 \\\\ 0 & 1 & 0 & 5 & 5 \\\\ 0 & 2 & 0 & -2 & -3 & -4 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) i-το 1/3 \\ cdot ΙΙ \\\\ \\ PHANTOM (0) \\\\ ΙΙΙ-2 \\ cdot ΙΙ \\\\\\ Phantom (0) \\ END (Array) \\ Rightarrow \\\\ \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 2/3 & 0 & 0 & 5 & 5 \\\\ 0 & 0 & 7 & -9 & -25 \\\\ 0 & 0 & -2 & -3 & -4 \\ END (Array) \\ Δεξιά). $$.

Τρίτο βήμα

Προχωρούμε στην επεξεργασία της τρίτης στήλης. Ως στοιχείο ανάλυσης, συμφωνήσαμε να λάβουμε τα διαγώνια στοιχεία της μήτρας συστήματος. Για το τρίτο βήμα, αυτό σημαίνει την επιλογή ενός στοιχείου που βρίσκεται στην τρίτη γραμμή. Ωστόσο, εάν απλά πάρουμε το στοιχείο 7 ως ψήφισμα, τότε ολόκληρη η τρίτη γραμμή θα πρέπει να διαιρέσει στις 7. Μου φαίνεται ότι είναι δυνατόν να χωριστεί η (-2) ευκολότερη. Επομένως, αλλάζουμε την τρίτη και τέταρτη γραμμή σε ορισμένες θέσεις και στη συνέχεια το στοιχείο ανάλυσης θα είναι (-2):

$$ \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 2/3 & 0 & 0 & 5 & 5 \\\\ 0 & 0 & 5 & 5 \\\\ 0 & 0 & 7 & 5 & - 25 \\\\ 0 & 0 & -2 & -3 & -4 \\ END (Array) \\ Δεξιά) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 2/3 & 0 & -11 / 3 \\\\ 0 & 1 & 0 & 5 & 5 \\\\ 0 & 0 & -2 & -3 & -4 \\\\ 0 & 0 & 7 & -9 & -25 \\ END (Array) \\ Δεξιά) $$ .

Επιτρέποντας το στοιχείο - (-2). Διαχωρίζουμε την τρίτη γραμμή στο (-2) και επαναφέρετε τα αντίστοιχα στοιχεία της τρίτης στήλης:

$$ \\ αριστερά (\\ begin (array) (CCCC | C) 1 & 0 & 2/3 & 0 & 0 & 5 & 5 \\\\ 0 & 0 & -2 & - 2 & - 3 & -4 \\\\ 0 & 0 & 7 & -9 & -25 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) \\ PHANTOM (0) \\\\ \\ PHANTOM (0) \\\\ III :( -2) \\\\\\ Φάντασμα (0) \\ END (Array) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 2/3 & 0 & -11/3 \\\\ 0 & 1 & 0 & 5 & 5 \\\\ 0 & 0 & 1 & 3/2 & 2 \\, 25 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) I-2/3 \\ cdot III \\\\ \\ Phantom (0) \\\\ \\ Φάντασμα ( 0) \\\\ IV-7 \\ END cdot III \\ (Array) \\ Rightarrow \\\\\\\\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 0 & 0 & 5 & 5 \\\\ 0 & 0 & 1 & 3/2 & 2 & 0 & 0 & 0 & -39/2 & - 0 & 0 & 0 39 \\ END (Array) \\ Δεξιά). $$.

Τέταρτο βήμα

Πηγαίνετε στο μηδενισμό της τέταρτης στήλης. Το στοιχείο που επιτρέπει βρίσκεται στην τέταρτη γραμμή και ισούται με το αριθμό $ - \\ Frac (39) (2) $.

$$ \\ left (\\ begin (array) (CCCC | C) 1 & 0 & 0 & 0 & 5 & 5 \\\\ 0 & 0 & 1 & 3/2 & 2 \\\\ 0 & 0 & 0 END (Array) \\ δεξιά) \\ begin (Array) (L) \\ PHANTOM (0) \\\\ \\ PHANTOM (0) \\\\ \\ PHANTOM (0) \\\\ IV: \\ αριστερά (- \\ FRAC (39) (2) \\ Δεξιά) \\ END (Array) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 0 & -1 & -5 \\\\ 0 & 1 & 0 & 5 & 5 \\\\ 0 & 0 & 1 & 3 & 1 & 2 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) Ι + IV \\\\ Π-5 \\ cdot IV \\\\ III-3/2 \\ cdot IV \\\\ \\ PHANTOM (0) \\ END (Array) \\ Rightarrow \\\\ \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCC | C) 1 & 0 & 0 & 0 & 0 & -5 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 2 \\ End (Array) \\ Δεξιά). $$.

Η απόφαση έχει τελειώσει. Η απάντηση είναι: $ x_1 \u003d -3 $, $ x_2 \u003d -5 $, $ x_3 \u003d -1 $, $ x_4 \u003d $ 2. Πλήρης λύση χωρίς εξήγηση:

Απάντηση: $ x_1 \u003d -3 $, $ x_2 \u003d -5 $, $ x_3 \u003d -1 $, $ x_4 \u003d $ 2.

Παράδειγμα αριθμού 3.

Επίλυση $ \\ αριστερά \\ (\\ begin (ευθυγραμμισμένη) & x_1-2x_2 + 3x_3 + 4x_5 \u003d -5? \\\\ & 2x_1 + x_2 + 5x_3 + 2x_4 + 9x_5 \u003d -3? \\\\ & 3x_1 + 4x_2 + 7x_3 + 4x_4 + 14X_5 \u003d -1? \\\\ & 2x_1-4x_2 + 6x_3 + 11x_5 \u003d 2? \\\\ & -2x_1 + 14x_2-8x_3 + 4x_4-7x_5 \u003d 20? \\\\ & -4x_1-7x_2-9x_3-6x_4-21x_5 \u003d - 9 . \\ Τέλος (ευθυγραμμισμένη) \\ δεξιά. $ Gaussa-jordan. Εάν το σύστημα είναι αβέβαιο, καθορίστε τη βασική λύση.

Τέτοια παραδείγματα αντιμετωπίζονται με το θέμα "Γενικές και βασικές λύσεις Slava". Στο δεύτερο μέρος του προαναφερθέντος θέματος Αυτό το παράδειγμα Επίλυση χρησιμοποιώντας τη μέθοδο Gauss. Το λύτουμε χρησιμοποιώντας τη μέθοδο Gaussa-Jordan. Ένα βήμα προς βήμα δεν θα είναι μια απόφαση, καθώς έχει ήδη γίνει σε προηγούμενα παραδείγματα.

$$ \\ ΑΡΙΣΤΕΡΑ (\\ begin (Array) (CCCCC | C) 1 & -2 & 3 & 0 & 4 & 2 & 9 & -3 & 1 & 5 & 2 & 7 & 7 & 4 & 14 & 0 & 11 & 2 & 4 & 6 & 0 & 11 & 4 & -7 & 20 & -7 & -7 & -9 & -6 & -7 & -9 -21 & -9 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) \\ Phantom (0) \\\\ ΙΙ-2 \\ cdot Ι \\\\ ΙΙΙ-3 \\ cdot Ι \\\\ IV-2 \\ cdot Ι \\\\ V + 2 \\ cdot Ι \\\\ VI + 4 \\ cdot Ι \\ END (Array) \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCCC | C) 1 & -2 & 3 & 0 & 4 & -5 \\ \\ 0 & 5 & -1 & 2 & 1 & 7 & 2 & 14 \\\\ 0 & 0 & 0 & 0 & 3 & 12 \\\\ 0 & 10 & -2 & 4 & 1 & 10 \\\\ 0 & -15 & 3 & -6 & -5 & -29 \\ END (Array ) \\ δεξιά) \\ Αρχίστε (Array) (L) \\ PHANTOM (0) \\\\ II: 5 \\\\ \\ Phantom (0) \\\\ \\ Phantom (0) \\\\ \\ PHANTOM (0) \\\\ \\ PHANTOM (0) \\ END (Array) \\ Rightarrow \\\\ \\ αριστερά (\\ begin (Array) (CCCCC | C) 1 & - 2 & 3 & 1 & -1/5 & 2/5 & 1/5 & 7/5 & 2 & 1 & 10 & -2 & 4 & 2 & 14 \\\\ 0 & 0 & 0 & 3 & 3 & 12 & 1 & 10 \\\\ 0 & -15 & 3 & 10 & -5 & -29 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) Ι + 2 \\ cdot II \\\\ \\ PHANTOM (0) \\\\ ΙΙΙ-10 \\ cdot II \\\\ IV: 3 \\\\ V-10 \\ cdot II \\\\ VI + 15 \\ cdot ΙΙ \\ ΕΔ (Array) \\ Rightarrow \\ Αριστερά (\\ Ξεκινήστε (ARRAY) (CCCCC | C) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5 \\\\ 0 & 1 & -1/5 & 2/5 & 1 / 5 & 7/5 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -1 & -4 \\\\ 0 & -1 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & -8 \\ END (ARTAY) \\ Δεξιά). $$.

Πιστεύω ότι ένας από τους μετασχηματισμούς που έγιναν ακόμα απαιτεί εξηγήσεις: $ IV: $ 3. Όλα τα στοιχεία της τέταρτης γραμμής μοιράστηκαν τρεις, τόσο καθαρά για λόγους απλούστευσης, χωρίσουμε όλα τα στοιχεία αυτής της γραμμής σε τρία. Η τρίτη γραμμή στη μεταρρυθμισμένη μήτρα έχει γίνει μηδέν. Απελευθερώστε τη γραμμή μηδέν:

$$ \\ left (\\ begin (array) (CCCCC | C) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5 \\\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & -8 \\ END (Array) \\ δεξιά) $$

Ήρθε η ώρα να πάμε στο τρίτο βήμα, στο οποίο πρέπει να επαναφερθούν τα στοιχεία της τρίτης στήλης. Ωστόσο, το διαγώνιο στοιχείο (τρίτη γραμμή) είναι μηδέν. Και δεν θα υπάρξει τίποτα να αλλάξει τις θέσεις των σειρών. Έχουμε ήδη χρησιμοποιήσει την πρώτη και τη δεύτερη γραμμή, έτσι δεν μπορούμε να τα αγγίξουμε. Και η τέταρτη και πέμπτη γραμμή έχει νόημα, για το πρόβλημα της ισότητας μηδέν του στοιχείου ανάλυσης δεν πηγαίνει οπουδήποτε.

Σε αυτή την περίπτωση, το πρόβλημα επιλύεται εξαιρετικά απλό. Δεν μπορούμε να αντιμετωπίσουμε την τρίτη στήλη; Λοιπόν, μετακινώντας στο τέταρτο. Ίσως, στην τέταρτη στήλη, το στοιχείο της τρίτης γραμμής δεν θα είναι μηδέν. Ωστόσο, η τέταρτη στήλη "άρρωστος" το ίδιο πρόβλημα με το τρίτο. Το στοιχείο τρίτης σειράς στην τέταρτη στήλη είναι μηδέν. Και η αλλαγή των καθισμάτων των γραμμών και πάλι, τίποτα δεν θα δώσει τίποτα. Η τέταρτη στήλη επίσης δεν μπορεί επίσης να επεξεργαστεί; Εντάξει, ας στραφούμε στο πέμπτο. Αλλά στην πέμπτη στήλη, το στοιχείο της τρίτης γραμμής δεν είναι καν ίση με το μηδέν. Είναι ίσο με ένα, το οποίο είναι πολύ καλό. Έτσι, το στοιχείο που επιτρέπει στην πέμπτη στήλη είναι 1. Επιλέγεται το επιτρεπτικό στοιχείο, οπότε πραγματοποιούμε τους πιο απομακρυσμένους μετασχηματισμούς της μεθόδου Gauss-Ιορδάνη:

$$ \\ left (\\ begin (array) (CCCCC | C) 1 & 0 & 13/5 & 4/5 & 22/5 & -11/5 \\\\ 0 & 1 & -1/5 & 2/5 & 1/5 & 7/5 \\\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & -2 & -8 \\ END (Array) \\ Δεξιά) \\ Αρχίστε (Array) (L) I-22/5 \\ cdot III \\\\ II-5.1 \\ cdot III \\\\ \\ PHANTOM (0) \\\\ IV + III \\\\ V + \\ cdot III \\ END (Array) 2 \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCCC | C) 1 & 0 & 13/5 & 4/5 & 0 & -99/5 \\\\ 0 & 1 & -1/5 & 2/5 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 0 \\ END (Array) \\ Δεξιά) \\ Rightarrow \\ \\ \\ Rightarrow \\ αριστερά | \\ Κείμενο (Αφαιρέστε το μηδέν γραμμές) \\ Δεξιά | \\ Rightarrow \\ αριστερά (\\ begin (Array) (CCCCC | C) 1 & 0 & 13/5 & 4/5 & 0 & -99/5 \\ \\ 0 & 1 & 3/5 & 0 & 0 & 0 & 0 & 1 & 4 \\ End (Array) \\ δεξιά) $$.

Οδήγησε τη μήτρα του συστήματος και μια εκτεταμένη μήτρα συστήματος σε μια βαθμίδα. Οι τάξεις και των δύο μήτρων είναι ίσες με $ r \u003d $ 3, δηλ. Είναι απαραίτητο να επιλέξετε 3 βασικές μεταβλητές. Ο αριθμός των άγνωστων $ n \u003d $ 5, έτσι πρέπει να επιλέξετε $ n-r \u003d 2 $ δωρεάν μεταβλητές. Από το $ r< n$, то согласно следствию из теоремы Кронекера-Капелли Αυτό το σύστημα Είναι αβέβαιο (δηλ. Έχει έναν άπειρο αριθμό λύσεων). Για να βρείτε λύσεις του συστήματος, κάντε ένα "βήματα":

Στα "βήματα" υπάρχουν στοιχεία από στήλες №1, №2, №5. Επομένως, η βασική θα είναι μεταβλητές $ x_1 $, $ x_2 $, $ x_5 $. Δωρεάν μεταβλητές, αντίστοιχα, θα είναι $ x_3 $, $ x_4 $. Στήλες №3 και №4, που αντιστοιχούν σε ελεύθερες μεταβλητές, υποφέρουν ως γραμμή, ενώ, φυσικά, χωρίς να ξεχνάμε να αλλάξουν τα σημάδια τους.

$$ \\ Αριστερά (\\ Ξεκινήστε (Array) (CCCCC | C) 1 & 0 & 05 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 3/5 \\\\ 0 & 0 & 0 & 1 & 4 \\ End (Array) \\ Δεξιά) \\ Rightarrow \\ αριστερά (\\ begin (Array) (ΚΤΚ | CCC) 1 & 0 & 0 & -99/5 & -13 / 5 & -4/5 \\\\ 0 & 1 & 0 & 3/5 & 1/5 & -2/5 \\\\ 0 & 0 & 1 & 4 & 0 & 0 \\ END (Array) \\ Δεξιά). $$.

Από την τελευταία μήτρα λαμβάνουμε μια γενική λύση: $ \\ αριστερά \\ (\\ ξεκινά (ευθυγραμμισμένη) & x_1 \u003d - \\ frac (99) (5) - \\ frac (13) (5) x_3- \\ frac (4) (5) ) x_4? \\\\ & x_2 \u003d \\ FRAC (3) (5) + \\ FRAC (1) (5) X_3- \\ FRAC (2) (5) x_4? \\\\ & x_3 \\ σε r? \\\\ & x_4 \\ το r? \\\\ & x_5 \u003d 4. \\ END (Αδεσμεύτων) \\ Δεξιά $ Η λύση βάση θα βρείτε με τη λήψη ελεύθερες μεταβλητές με μηδέν, δηλαδή $ x_3 \u003d 0 $, $ x_4 \u003d 0 $..:

$$ \\ Αριστερά \\ (\\ Ξεκινήστε (ευθυγραμμισμένο) & x_1 \u003d - \\ Frac (99) (5); \\\\ & X_2 \u003d \\ Frac (3) (5); \\\\ & X_3 \u003d 0; \\\\ & X_4 \u003d 0; \\\\ & X_3 \u003d 0; 0; \\\\ & x_5 \u003d 4. \\ end (ευθυγραμμισμένο) \\ σωστό. $$

Η εργασία επιλύεται, παραμένει μόνο για να καταγράψει την απάντηση.

Απάντηση: Γενική λύση: $ \\ Αριστερά \\ (\\ Ξεκινήστε (ευθυγραμμισμένο) & X_1 \u003d - \\ Frac (99) (5) - \\ Frac (13) (5) x_3- \\ Frac (4) (5) x_4; \\\\ & X_2 \u003d \\ frac (3) (5) + \\ frac (1) (5) x_3- \\ frac (2) (5) x_4; \\\\ & x_3 \\ in r; \\\\ & x_4 \\ in r; \\\\ & x_5 \u003d 4. \\ end (ευθυγραμμισμένες) \\ right $, βασική λύση:. $ \\ αριστερό \\ (\\ begin (ευθυγραμμισμένες) και x_1 \u003d - \\ FRAC (99) (5)? \u200b\u200b\\\\ & x_2 \u003d \\ FRAC (3) (5) · \\\\ \\ x_3 \u003d 0; \\\\ & x_4 \u003d 0; \\ ed (ευθυγραμμισμένη) \\ Δεξιά. $.

Δείτε επίσης: V2: DE 57 - ένα θεμελιώδες σύστημα λύσεων γραμμικής ομοιογενούς διαφορικής εξίσωσης B1 2. Ο γραμμικός χειριστής στον πεπερασμένο χώρο διαστάσεων, τη μήτρα του. Χαρακτηριστικό πολυωνυμικό γραμμικό χειριστή. Τους αριθμούς και τους διανύσματα των γατών. Βασικές δομές ελέγχου διαρθρωτικού προγραμματισμού Εισιτήριο 13 Γωνία μεταξύ 2 ίσων, συνθηκών παραλληλισμού και κάθετα. Μετατρέποντας έναν γραμμικό χειριστή κατά τη μετακίνηση σε μια νέα βάση Εισιτήριο 13. Γραμμικοί φορείς εκμετάλλευσης. Η μήτρα του γραμμικού χειριστή. Εισιτήριο 26. Υπουργεία ρίζας. Διάσπηση γραμμικού χώρου στο άμεσο άθροισμα των υπονομεύσεων ρίζας. Εισιτήριο 27. Ιορδανία και Matrix Jordanov ενός γραμμικού φορέα εκμετάλλευσης σε ένα πολύπλοκο χώρο. Εισιτήριο 35. Ερμίτικοι χειριστές και ερματική μήτρα. Ερμιτική αποσύνθεση ενός γραμμικού φορέα εκμετάλλευσης. Εισιτήριο 7 κλιμακωτά έργα τέχνης, προβολή ενός φορέα σε άλλο. Η έννοια του γραμμικού χώρου και του υποενίγματος, κριτηρίων υπόγειου χώρου

Θεώρημα (για την επιλογή ενός στοιχείου ανάλυσης)

Εάν υπάρχουν αρνητικά στοιχεία σε αρκετές στήλες Z-Stroke, τότε η εξουσιοδοτημένη στήλη θα πρέπει να επιλέξετε μία στήλη στην οποία το μέγιστο προϊόν της απόλυτης τιμής του συντελεστή στη σειρά Z-TH και της ελάχιστης αναλογίας απλού συστήματος αυτής της στήλης.

Απόδειξη:

Αφήστε το επιτρεπόμενο στοιχείο να επιτρέπεται. Ως αποτέλεσμα του βήματος τροποποιημένων εξαιρέσεων της Ιορδανίας, ένα ελεύθερο μέλος στη σειρά Z θα είναι ο αριθμός ίσος με το .poscolp και το βραχίονα σε αυτή την έκφραση θα είναι πάντα θετική. Και δεδομένου ότι η έννοια της λειτουργικότητας είναι πάντα ίση με ένα ελεύθερο μέλος, αυτό το βραχίονα είναι τα πρόσθετα στη λειτουργικότητα, η οποία λαμβάνεται ως αποτέλεσμα του βήματος που λαμβάνεται.

Όσο μεγαλύτερη είναι η αύξηση της λήψης της λειτουργικότητας σε κάθε βήμα, τα λιγότερα βήματα θα απαιτηθούν (δηλ. Υπολογιστές) για να επιτευχθούν optima. Το μέγεθος αυτής της αύξησης εξαρτάται από την απόλυτη τιμή του συντελεστή και του μεγέθους της μικρότερης σχέσης απλού. Δηλαδή, η εξουσιοδοτημένη στήλη θα είναι μια στήλη που έχει ένα μέγιστο προϊόν.

Παράδειγμα: Γραμμικός προγραμματισμός:

Βρίσκουμε τη μέγιστη λειτουργία

Με περιορισμούς

Λύση: Ας κάνουμε ένα τραπέζι με την Ιορδανία.

Δεδομένου ότι υπάρχουν δωρεάν μέλη σε αυτήν, το σχέδιο είναι αναφορά. Ωστόσο, δεν είναι βέλτιστη, αφού οι συντελεστές Z-Row είναι αρνητικοί. Επιλέξτε από αυτά που έχει το μεγαλύτερο προϊόν της απόλυτης αξίας και τη μικρότερη σχέση απλού. Η τρίτη στήλη θεωρεί ότι έχει τη μεγαλύτερη απόλυτη τιμή των Σχέσεων 8 και των Simplex: αντίστοιχα (επομένως, το στοιχείο 1 στην τρίτη στήλη θα επιλυθεί). Κάνουμε ένα βήμα τροποποιημένων εξαιρέσεων της Ιορδανίας και έρχονται στο επόμενο τραπέζι.

Κρίνοντας από τους συντελεστές Z-Row, η βέλτιστη λύση δεν επιτυγχάνεται στον πίνακα. Πάρτε τη δεύτερη στήλη με έναν αρνητικό συντελεστή στη γραμμή Z για την επιδίωξη (η συμβολοσειρά ανάλυσης μπορεί να είναι η πρώτη). Με το σημείο 5, κάνουμε το επόμενο βήμα.

Στη γραμμή Ζ, όλοι οι συντελεστές είναι θετικοί, το σχέδιο που λαμβάνεται με την εξισώνοντας τις ανώτερες μεταβλητές μηδέν και τα πλευρικά μέλη, είναι βέλτιστη. Γράφουμε τις αξίες των κύριων άγνωστων από τον πίνακα: Θεωρούμε τη μέγιστη τιμή του λειτουργικού στο τελευταίο πίνακα κυττάρων:

Στον τελικό πίνακα, όλοι οι καθοριστικοί παράγοντες είναι μη αρνητικοί. Αυτό υποδηλώνει ότι με τις αξίες της άγνωστης λειτουργικότητας φτάσει σε ένα μέγιστο

Συνήθως θεωρείται ότι δεν υπάρχουν σημεία σχετικά με το σύνολο των σχεδίων του προβλήματος, στο οποίο ο παρονομαστής στόχος είναι μηδέν. Χωρίς τον περιορισμό της γενικότητας, μπορούμε να το υποθέσουμε αυτό.

Στο πρόβλημα του κλασματικού γραμμικού προγραμματισμού, το άκρο της λειτουργίας στόχου επιτυγχάνεται στην κορυφή των λύσεων πολυεδρών. Αυτή η ομοιότητα με τον γραμμικό προγραμματισμό σάς επιτρέπει να λύσετε κλασματικές γραμμικές εργασίες από το βήμα με τη μέθοδο.

Οι υπολογισμοί γίνονται με τη μορφή πινάκων της Ιορδανίας. Ταυτόχρονα, δύο κατώτατες γραμμές απορρίπτονται για τη λειτουργική: στο πρώτο από αυτά, γράψτε τους συντελεστές του αριθμητή και στον δεύτερο-παρονομαστή. Η εργασία προέλευσης αντιστοιχεί στον Πίνακα 1:

	–Χ. 1	–Χ. 2	…	–x J.	…	–x N.
y. 1	ΕΝΑ. 11	ΕΝΑ. 12	…	ΕΝΑ. 1 Ι.	…	ΕΝΑ. 1 Ν.	ΕΝΑ. 1
…	………………………………………	…
y i.	Ένα i. 1	Ένα i. 2	…	ένα ij.	…	Α στο.	Ένα i.
…	………………………………………	…
y m	ΕΙΜΑΙ. 1	ΕΙΜΑΙ. 2	…	Ένα mj.	…	Ένα mn.	ΕΙΜΑΙ.
z. 1	–Π. 1	–Π. 2	…	–p J.	…	–p N.
z. 2	–q. 1	–q. 2	…	–q J.	…	–q N.

Διά μέσου y i. Οι διαφορές μεταξύ του δεξιού και του αριστερού τμημάτων του συστήματος περιορισμών αναφέρονται:

Y i.= Ένα i.– Ένα i. 1 Χ. 1 – Ένα i. 2 Χ. 2 – Ένα i. 3 Χ. 3 – … – ένα στο x n ³ 0.

Με δωρεάν μεταβλητές, θα καλέσουμε τις μεταβλητές που βρίσκονται στην επάνω γραμμή τίτλου του πίνακα της Ιορδανίας. Δίνοντας μια ελεύθερη μεταβλητή μηδενική τιμή, παίρνουμε την αρχική λύση βάσης :. Αυτός ο φορέας δεν μπορεί να αποτελέσει σχέδιο υποστήριξης, επειδή Ο στόχος λειτουργικός παρονομαστής σε αυτό είναι μηδέν ( z. 2 \u003d 0). Επομένως, μεταξύ των ελεύθερων μελών του συστήματος περιορισμών ΕΝΑ. 1 ,…, ΕΙΜΑΙ. Βεβαιωθείτε ότι έχετε αρνητικούς αριθμούς (διαφορετικά η βασική λύση θα είναι ένα σχέδιο στήριξης).

Τα βήματα των τροποποιημένων εξαιρέσεων της Ιορδανίας, όπως και όταν η επίλυση ενός γραμμικού προβλήματος προγραμματισμού (βλέπε), η εύρεση του αρχικού σχεδίου του προβλήματος. Σαν άποτέλεσμα Κ. Βήματα που φτάνουμε στον Πίνακα 2:

	–y. 1	…	–x J.	…	–x N.
Χ. 1	ΣΙ. 11	…	ΣΙ. 1 Ι.	…	ΣΙ. 1 Ν.	ΣΙ. 1
.…	………………………………………
y i.	b i. 1	…	b ij.	…	Β	b i.
….	…………………………………….
y m	b m. 1	…	b mj.	…	b mn.	b m.
z. 1	ΦΑ. 1	…	f j.	…	f N.	ΦΑ.
z. 2	ΣΟΛ. 1	…	g J.	…	g n.	ΣΟΛ.

Πίνακας 2 Όλα τα ελεύθερα μέλη b i. Μη αρνητική, η οποία παρέχει μη μόνιμες βασικές μεταβλητές Χ. 1 ,…, y m. Επιπλέον (λόγω της θετικότητας του παρονομαστή της λειτουργίας στόχου z. 2 σχετικά με το σύνολο των σχεδίων αναφοράς). Το αρχικό σχέδιο στήριξης είναι ο φορέας με συντεταγμένες. Η αξία της λειτουργίας στόχου στο αρχικό σχέδιο αναφοράς είναι ίσο.

Σημειώστε ότι αν σε ένα από τα βήματα των εξαιρέσεων της Ιορδανίας από οποιοδήποτε από τα ελεύθερα μέλη ΣΙ. Θα είμαι αρνητικός, και όλα τα άλλα στοιχεία ΕΓΩ.- Οι σειρές θα είναι μη αρνητικές, η εργασία δεν θα έχει λύσεις λόγω έλλειψης σχεδίων.

Ακολουθήστε τη λειτουργία στόχου κατά τη μετάβαση από ένα σχέδιο αναφοράς στο άλλο. Αποδεικνύεται ότι το σήμα διαφοράς μεταξύ των νέων και των παλαιών τιμών της λειτουργίας συμπίπτει με το σημάδι του καθοριστικού παράγοντα. Αν ένα. Επειδή Η λύση Polyhedron περιέχει μόνο έναν πεπερασμένο αριθμό σχεδίων υποστήριξης, τότε για τον τελικό αριθμό βημάτων που θα έρθουμε στο βέλτιστο σχέδιο αναφοράς.

Αυτή η διαδικασία μπορεί επίσης να παρεμβαίνει στην απεριόριστη πολυεδρική λύσεις. Στην περίπτωση αυτή, η λειτουργία στόχου μπορεί να έχει το λεγόμενο ασυμπτωτικό άκρο (στην περίπτωση αυτή, το μέγιστο). Το ασυμπτωτικό μέγιστο καθήκον του κλασματικού γραμμικού προγραμματισμού είναι η ακριβής ανώτερη πτυχή της λειτουργίας στόχου σε μια ποικιλία σχεδίων, η οποία δεν επιτυγχάνεται σε κανένα από τα σχέδια. Στην περίπτωση που το έργο έχει ένα ασυμπτωτικό μέγιστο, στην περιοχή των σχεδίων, μπορείτε πάντα να βρείτε ένα τέτοιο σχέδιο (όχι αναφορά), στο οποίο η λειτουργία στόχος παίρνει την τιμή ενός αυθαίρετα κοντά στο ασυμπτωτικό μέγιστο.

Η μέθοδος Pistower σάς επιτρέπει να βρείτε όχι μόνο το μέγιστο, αλλά και το ασυμπτωτικό μέγιστο πρόβλημα του κλασματικού γραμμικού προγραμματισμού. Σκεφτείτε λεπτομερέστερα τη μετάβαση από το σχέδιο να σχεδιάσετε και να μάθετε. Επιλέγοντας το στοιχείο που επιτρέπει Ι.- Στήλη, πρέπει να καθοδηγούμε από την αρχή της ελάχιστης σχέσης απλής απλή. Εκείνοι. Επίλυση στοιχείου Β. Ι.- Η στήλη θα πρέπει να μπει στη γραμμή για την οποία η σχέση simplex είναι θετική και ελάχιστη.

Επειδή Αφού βρούμε το αρχικό σχέδιο στήριξης όλων των σωστών τμημάτων b i. έχουν γίνει μη αρνητικές, τότε ένα στοιχείο ανάλυσης Ι.Η στήλη μπορεί να είναι ένα από τα θετικά του στοιχεία (). Εάν σε κάθε στάδιο του σταδίου της εύρεσης, το βέλτιστο σχέδιο αναφοράς στην επιλεγμένη στήλη ανάλυσης υπάρχει (τουλάχιστον ένα) θετικό στοιχείο, τότε μια τέτοια εργασία έχει ένα μέγιστο (είναι δυνατόν να μην).

Ωστόσο, εάν σε ένα από τα βήματα κάποια εκτίμηση είναι μικρότερη από το μηδέν, και με όλα τα στοιχεία Ι.- στήλη. Στη συνέχεια, σε αυτή τη στήλη, καθοδηγούμενη από την αρχή της ελάχιστης σχέσης απλού, δεν μπορεί να επιλεγεί το στοιχείο που επιτρέπει. Αύξηση των τιμών της ελεύθερης μεταβλητής x J. Από 0 και έως (βλ. Πίνακα 2), όλοι παραμένουμε στον τομέα των σχεδίων. Αυτό οφείλεται στο γεγονός ότι η αύξηση της μεταβλητής x J. Δεν προκαλεί σήμα αλλαγής σε μείον οποιαδήποτε από τις βασικές μεταβλητές.

Δηλώνει Μ. Το όριο στον οποίο, μονοτονικά, το αντικείμενο προσπαθεί η λειτουργία στόχου στη διεύθυνση :. Αυτός ο αριθμός είναι ένα ασυμπτωτικό μέγιστο.

| 2 |