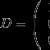Schéma výpočtu. „Vývoj algoritmov VBA. Bloková schéma. Štruktúry algoritmov. Vstupné a výstupné operátory v programovacom jazyku Pascal

Každodenný život každého človeka zahŕňa riešenie obrovského množstva úloh rôznej zložitosti v práci alebo pri štúdiu. Niektoré úlohy sú také jednoduché, že keď ich vykonávame, robíme určité činnosti automaticky, bez toho, aby sme o tom premýšľali. Riešenie akéhokoľvek problému, dokonca aj toho najjednoduchšieho, sa zvyčajne vykonáva postupne v niekoľkých krokoch. Tento druh postupnosti pri riešení problémov sa nazýva algoritmus. Dnes sa pozrieme na to, čo sú to lineárne algoritmy, ako je znázornená ich štruktúra, ako sa riešia a programujú.

Algoritmický jazyk

Tento koncept je presnou inštrukciou pre interpreta, aby vykonal určitú postupnosť akcií, ktorá je zameraná na vyriešenie úlohy.

Tento jazyk je prostriedkom na opis algoritmov, ktoré sú zvyčajne orientované na používateľa.

• Blok začiatku a konca algoritmu. Na bloku je nápis „začiatok“ alebo „koniec“.
• Blok vstupu/výstupu dát. Tento blok je znázornený ako rovnobežník. Sú na ňom umiestnené tieto nápisy: „vstup“, „výstup“, „tlač“. Sú tiež sprevádzané zoznamom vstupných alebo výstupných premenných.
• Aritmetický blok alebo rozhodovací blok. Zodpovedá obdĺžniku. Blok by mal mať nápis: „operácia“, „skupina operácií“.

Pomocou takýchto blokových schém je znázornené riešenie lineárnych algoritmov. Ďalej si povieme niečo o vlastnostiach priraďovania hodnôt.

Lineárne výpočtové algoritmy

Hlavnou elementárnou akciou vo výpočtovom algoritme je priradenie určitej hodnoty premennej. V prípade, že hodnota konštanty je určená typom jej zápisu, hodnota premennej získa konkrétnu hodnotu výlučne ako výsledok priradenia. Dá sa to urobiť dvoma spôsobmi: pomocou príkazu priradenia; pomocou vstupného príkazu.

Príklad riešenia lineárneho algoritmu

Uveďme príklad popisu pravidiel delenia obyčajných zlomkov pomocou lineárneho algoritmu, ktoré majú v školských učebniciach nasledujúci obsah:

• čitateľ zlomku 1 musí byť vynásobený menovateľom zlomku 2;
• menovateľ zlomku 1 musí byť vynásobený čitateľom zlomku 2;
• musíte si zapísať zlomok, v ktorom je čitateľ výsledkom dosiahnutia 1 bodu a menovateľ je výsledkom dosiahnutia 2 bodov. Algebraická forma tohto pravidla je nasledovná:

a/b: c/d=(a*d)/(b*d)=m/n.

Poďme teda zostaviť algoritmus na delenie zlomkov pre počítač. Aby sme sa nemýlili, použijeme rovnaký zápis premenných ako vo vzorci uvedenom vyššie. a, b, c, d - zdrojové údaje vo forme celočíselných premenných. Výsledkom budú tiež celočíselné hodnoty. Riešenie v algoritmickom jazyku bude nasledovné:

alg Delenie zlomkov

neporušené a, b, c, d, m, n

vstup a, b, c, d

kon

Grafická podoba riešenia

Schéma lineárneho algoritmu opísaného vyššie vyzerá takto:

Príkaz priradenia hodnoty má nasledujúci formát:

Premenná:=výraz.

Znak „:=“ sa číta ako priradiť.

Priradenie je príkaz, ktorý počítač potrebuje na vykonanie nasledujúcich akcií:

• výpočty výrazov;
• priradenie výslednej hodnoty premennej.

Vyššie uvedený algoritmus obsahuje dva príkazy ako priradenie. V blokovej schéme musí byť priraďovacia inštrukcia napísaná v obdĺžniku nazývanom výpočtový blok.

Pri popise lineárnych algoritmov nie je potrebné striktne dodržiavať prísne pravidlá pri písaní výrazov. Môžete ich napísať pomocou obvyklého matematického formulára. Koniec koncov, toto nie je striktná syntax programovacieho jazyka.

V uvedenom príklade algoritmu je tiež vstupný príkaz:

Zadajte a, b, c, d.

Vstupný príkaz v blokovej schéme je zapísaný v paralelograme, teda vo vstupno-výstupnom bloku. Vykonaním tohto príkazu procesor preruší činnosť, kým používateľ nevykoná určité akcie. Konkrétne: používateľ musí zadať vstupné premenné (ich hodnoty) na (klávesnici) a stlačiť Enter, ktorý funguje ako kláves enter. Je dôležité, aby boli hodnoty zadané v rovnakom poradí ako zodpovedajúce premenné umiestnené vo vstupnom zozname.

Lineárny algoritmus. Jeho programovanie

Ako už bolo spomenuté na začiatku článku, lineárne programy môžu obsahovať nasledujúce vyhlásenia:

• zadanie;
• vstup;
• záver.

To znamená, že pomocou uvedených operátorov sa implementujú algoritmy.

Takže v programovacom jazyku je to napísané takto:

NECH A = B, kde A je premenná, B je výraz. Napríklad A = Y + 20.

Vstupný príkaz vyzerá takto:

INPUT, napríklad: INPUT C

Operátor pre výstup údajov, hodnôt, je napísaný v nasledujúcom tvare:

TLAČIŤ. Napríklad PRINT S.

Uveďme si jednoduchý príklad. Musíme napísať program, ktorý nájde súčet čísel A a B zadaných z klávesnice.

V programovacom jazyku dostaneme program, ktorého text je uvedený nižšie.

Vstupné a výstupné operátory v programovacom jazyku Pascal

Pascal neposkytuje špeciálne operátory na označenie vstupných alebo výstupných operácií, ktoré používajú lineárne algoritmy. V programoch sa informácie vymieňajú pomocou vstavaných postupov. Keďže nie je potrebný predbežný popis štandardného postupu, je dostupný každému programu, ktorý obsahuje jeho volanie. Spomínaný názov postupu tiež nie je žiadnym vyhradeným slovom.

Pri zadávaní údajov sa takéto operátory používajú na odkazovanie na štandardný postup zadávania údajov, ktorý je už zabudovaný v programe.

Čítanie (A, B, C), kde A, B, C sú premenné, ktoré je potrebné zadať do pamäte RAM na zapamätanie.

Readlnn (x1, y, x2) - po ukončení zadávania sa kurzor presunie na začiatok nového riadku.

Readlnn; - označuje, že čakáte na stlačenie tlačidla „Enter“. Zvyčajne sa tento príkaz vkladá do textu pred posledný „Koniec“, aby sa uložili výsledky vykonávania programu na obrazovke s obsahom.

Údaje sa zobrazujú na obrazovke monitora pomocou nasledujúcich operátorov:

Zápis (A, B, C) - zadaním hodnôt A, B, C v jednom riadku kurzor neopustí aktuálny riadok.

Writeln (z, y, z2) - po dokončení výstupu hodnôt sa kurzor na tejto pozícii presunie na nový riadok.

Writeln; - označuje preskočenie jedného riadku a prechod na začiatok nového.

S pomocou takýchto jednoduchých operátorov sa údaje zadávajú a vydávajú v jazyku Pascal.

zhrnutie ďalších prezentácií

„Základné algoritmické štruktúry“ - Vykonávanie príkazov „telo slučky“. Bloková schéma "vetvenia" algoritmickej štruktúry. Nech n=5; i=4. Bloková schéma cyklického algoritmu. Koniec. Algoritmická štruktúra "výber". Nech n=5; i=5. Štart. Štruktúra vetvenia. Nech n=5; i=6. Základné typy algoritmických štruktúr. Algoritmická štruktúra "cyklus". Kladné číslo. Vývojový diagram algoritmickej štruktúry „výberu“. Bloková schéma lineárneho algoritmu.

„Typy algoritmov“ - Upratovanie bytu. Otvorte vrecko. Motto lekcie. Hanojské veže. Názov postavy. Pozrite si karikatúru. Zbierajte úrodu. Úvod do algoritmu. Priblížte sa k prechodu. Cyklické algoritmy. Vojdite do záhrady. Palmy. Algoritmus ľudských akcií. Grafický diktát. Algoritmy nahrávania. Algoritmus.

Zaznamenávanie cyklu v procedúre. Oprava postupu. Primárne farby. Nakreslíme stenu. Čo je to algoritmus? Tím. Interaktívny tutoriál. Kreslenie strechy. Nakreslíme dom. Poďme kresliť. Kreslíme okná. Dom je pripravený. Cyklus. Vedomosti. Zmeňte farbu pera.

„Problémy s lineárnym algoritmom“ - X = 0 Neexistujú žiadne riešenia. Y = 2. X = 3 Y = 1/48. Sú uvedené súradnice vrcholov trojuholníka ABC. Vypočítajte hodnotu funkcie Y pri X=2 pomocou vývojového diagramu algoritmu. Previesť A na väčšie jednotky informácií. Algoritmizácia je proces vývoja algoritmu (akčného plánu) na riešenie problému. X = -1 Neexistujú žiadne riešenia. Príklady riešenia problémov. Uvedené sú dĺžky strán trojuholníka A, B, C. Nájdite oblasť trojuholníka S. Vytvorte blokovú schému algoritmu na riešenie problému.

„Algoritmické konštrukcie“ - Metóda znázornenia algoritmov vo forme grafu. Vetvenie. Prezentácia algoritmov vo forme popisu postupnosti akcií. Formy prezentácie algoritmov. Vývojový diagram algoritmu „tapety“. Algoritmické návrhy. Algoritmus na riešenie problému. Bloková schéma. Grafický spôsob prezentácie algoritmov. Metódy prezentácie algoritmov. Algoritmus. Komplexný algoritmus. Blokové schémy základných štruktúr.

"Hlavné typy algoritmických štruktúr" - Napíšte algoritmy vo verbálnej forme. Pracovať v skupinách. Štruktúra. Pravopis predpôn. Základné typy algoritmických štruktúr. Kontrola samostatnej práce. Fyzické cvičenie. Úlohy na upevnenie vedomostí. Algoritmus. Základná štruktúra. Nastavenie počiatočných parametrov. Recept na prípravu čaju. Vetvenie. Nájdite koreň. Slučka s dodatočnou podmienkou. Cyklus. Blokovať znaky. Koniec algoritmu. Hlavné typy agrorytmických štruktúr.

Všeobecné pokyny
Na syntézu obvodov v odd. 5.1 popisuje nasledujúce kroky:
1. Popis funkcie požadovaného obvodu.
2. Priradenie vstupných a výstupných premenných a priradenie hodnôt 0 a 1.
3. Zostavenie pravdivostnej tabuľky.
4. Stanovenie potrebných logických operácií.
5. Zjednodušenie a v prípade potreby transformácia obvodu.
Ak je známa pravdivostná tabuľka, potom je teraz vhodné začať 4. etapu s kompiláciou normálnej formy OR. Bude to maximálne zjednodušené pomocou Carnotovho diagramu. Na konci kroku 4 sa získa zjednodušená logická funkcia, ktorú možno použiť na zostavenie logického digitálneho obvodu.
Krok 5 kontroluje, či je možné a racionálne ďalšie zjednodušenie nájdenej funkcie pomocou logickej algebry. Ak áno, je potrebné vykonať zjednodušenie.
Teraz musíme zistiť, aké logické prvky sú k dispozícii. Logická funkcia musí byť transformovaná tak, aby obsahovala iba dostupné logické prvky. Potom môžete zostaviť obvod.

Digitálny obvod zapnutia/vypnutia z viacerých miest

Pomocou logických brán musíte syntetizovať obvod, ktorý funguje ako obvod zapnutia/vypnutia z viacerých miest. Stav výstupu by sa mal zmeniť iba vtedy, ak sa zmení stav jedného zo vstupov. Ak oba vstupy zmenia svoj stav, potom by sa výstupný stav nemal zmeniť. Obvod musí byť postavený na prvkoch OR-NOT.
Požadovaný obvod má dva vstupy a jeden výstup. Vstupné premenné sa nazývajú A a B. Výstupná premenná sa nazýva Z (obrázok 5.47).
Pravdivostná tabuľka obvodu s dvomi vstupnými premennými má 4 možnosti (obr. 5.48). Počiatočný stav Z pre prvú možnosť je možné nastaviť ľubovoľným spôsobom. Zvolené Z = 0.
Pri prechode z možnosti 1 na možnosť 2 zmení premenná A svoj stav. Premenná B nemení stav. Ak zmení stav iba jeden zo vstupov, potom podľa zadanej úlohy musí výstup Z zmeniť svoj stav. Z sa musí rovnať 1.
Pri prechode z možnosti 2 na možnosť 3 menia premenné A a B svoj stav. Z by sa nemalo meniť. Pri prechode z možnosti 3 na možnosť 4 zmení premenná A svoj stav z 0 na 1. B zostáva rovná 1. Z teda musí zmeniť stav z 1 na 0. Pravdivostná tabuľka je pripravená. Mohlo by to vyzerať inak, keby sme v možnosti 1 zvolili Z= 1.
Pre pravdivostnú tabuľku (obr. 5.48) si treba zapísať normálny tvar ALEBO. Vyzerá to takto:
Z = (AaB)w(AaB).
Ak do Carnotovho diagramu zadáte normálny tvar ALEBO, môžete vidieť, že ďalšie zjednodušenie nie je možné (obr. 5.49).
Pretože obvod musí byť postavený na prvkoch OR-HE, je potrebné transformovať rovnice:
Z = (AaB)w(AaB)-,
Z = (AaB)v(AaB),
Z = AaBaAaB.

Ryža. 5,50 Digitálny obvod

Obvod zostrojený podľa transformovanej rovnice je znázornený na obr. 5,50.

Dva z troch sa prepínajú

Systémy spojené so zvýšeným rizikom, ako napríklad jadrová elektráreň, musia byť v prípade havárie okamžite odstavené. Vypnutie prebieha automaticky pomocou digitálneho obvodu. V núdzových senzoroch zodpovedných za vypnutie sa môžu vyskytnúť falošné poplachy. Preto sú v každom kritickom mieste nainštalované tri identické havarijné snímače (obr. 5.51).
Vypnutie by malo nastať len vtedy, keď sa spustia aspoň dva z troch alarmových senzorov. Tento prístup zabraňuje zbytočným odstávkam systému, ktoré spôsobujú finančné straty. Po spustení majú núdzové senzory stav 1. Systém by sa mal vypnúť, ak je na výstupe okruhu aktívny stav 1.
Vyžaduje sa teda obvod, ktorého výstup je v stave 1, keď sú aspoň 2 z 3 vstupov v stave 1. Tento obvod sa nazýva spínač dvoch z troch.
Vstupné premenné sú pomenované A, B a C. Výstupná premenná je Z. Vytvorme pravdivostnú tabuľku pomocou slovného popisu princípu činnosti obvodu. Vždy, keď sa dve vstupné premenné rovnajú 1, Z = 1. Ak sú všetky tri vstupné premenné rovné 1, musí sa Z rovnať aj 1. Takáto pravdivostná tabuľka je na obr. 5.52.
Ďalej sa podľa zostavenej pravdivostnej tabuľky zapíše normálna forma OR:

Ryža. 5.51.

Z = (A a B a C) v (A a B a C) v a5aC|v(^aSaC).

Normálna forma OR je zjednodušená pomocou Carnotovho diagramu (obr. 5.53). Môžu byť vytvorené tri dvojité skupiny. Zjednodušená rovnica je:
Z = (AaB)w(BaC)w(AaC).
Pomocou tejto rovnice môžete zostaviť diagram (obr. 5.54).
Často sú po ruke iba prvky OR-HE. Na zostavenie obvodu s použitím iba prvkov OR-HE transformujeme rovnicu: na °-
Z = (AaB)v(BaC)v(AaC);
======= S O.
Z = (AlB)v (BaC)v (AlC);
—=====—= Obr. 5.55. Spínací okruh "dva"
Z = AlVlVlSlAlS. z troch" na prvkoch Sh1I-NE.
Príslušná schéma je znázornená na obr. 5.55.

Paritný obvod

Na detekciu chýb v kódoch (pozri časti 8.7 a 8.8), ako aj na úlohy riadenia a monitorovania je často potrebný obvod, v ktorom je výstup 1, keď je párny počet vstupov 1.
Tento obvod sa nazýva paritný obvod.
Je potrebné syntetizovať obvod so štyrmi vstupmi. Vstupné premenné sú A, B, C a D. Výstupná premenná je Y.
Najprv musíte vytvoriť pravdivú tabuľku. Y sa bude vždy rovnať 1, ak sa 0, 2 alebo 4 vstupné premenné rovnajú 1 (obrázok 5.56).
Z pravdivostnej tabuľky získame normálny tvar OR:
Y = (A l V lS l D)\/ ^ A l V lS l (A l V lS l (A l V aS l
v(A l V lS l [A l V lS l (A l V lS l (A l V lS l D).

Jednotlivé úplné spojky sú očíslované. Skúsme si normálnu formu OR zjednodušiť pomocou Karnaughovej mapy (obr. 5.57). Tu sa stretávame so zriedkavým prípadom, kedy je vytvorenie skupín nemožné. To znamená, že túto normálnu formu OR nemožno zjednodušiť a jej diagram je znázornený na obr. 5.58.

Prahový logický obvod je obvod, v ktorom musí mať určitý minimálny počet vstupných premenných stav 1, aby sa na výstupe objavila logická 1.
Napríklad musíte vypočítať obvod s piatimi vstupnými premennými. Výstup by mal byť 1 iba vtedy, keď sú aspoň 4 vstupy 1.
Vstupné premenné sú pomenované A, B, C, D a E. Výstupná premenná je Z. Najprv musíme definovať pravdivostnú tabuľku. S piatimi premennými je možných 32 možností (obr. 5.59):
Z =¦ (A l V lS l D l E^v (A l V lS l D l E)v (A l V lS l D l v^A l V lS l D l E^v [A l V lS l Dl E^v (A l B lS l D l E).
Normálny tvar OR pozostáva zo šiestich úplných spojok.
Normálna forma OR je zjednodušená pomocou Carnotovho diagramu (obr. 5.60). Môžete vytvoriť 5 dvojitých skupín. Výsledkom je nasledujúca zjednodušená logická funkcia:
Z = (A aBaCaE)v (A aBaDaE)v (A aBaCaD)v v(A aC a D a E)v (B aC a D a E).

Schéma pre zjednodušenú funkciu je znázornená na obr. 5.61. Táto rovnica môže byť ďalej zjednodušená pomocou algebry logiky. Pre prvé tri úplné spojky môžeme vyradiť zo zátvoriek (AaB), pre posledné dve - (C l D). Výsledná funkcia je:
Z = [(A A B) A ((CA E) V (D A E) A CA X>))] V [(CA D) A ((A A E) V (BA Z))]. Napriek tomu nebolo možné dosiahnuť výrazné zjednodušenie.

Porovnávací obvod (komparátor)

V digitálnej technike je často potrebné porovnávať digitálne dáta medzi sebou. Najjednoduchší porovnávací obvod, takzvaný komparátor, porovnáva stav dvoch premenných navzájom.
Nech sú premenné označené A a B. A a B sa môžu rovnať. A môže byť väčšie ako B a naopak. Komparátor má tri výstupy pre tieto tri možné možnosti. Sú označené X, Y a Z a ich stavy sú priradené takto:
A = Z => X = 1;
A > B^ > Y= 1;
A< В =>Z = 1.
Preto je potrebné syntetizovať obvod s dvoma vstupnými premennými A a B a výstupnými premennými X, Y a Z.
Pri vytváraní pravdivostnej tabuľky by ste sa mali riadiť pravidlami: A je väčšie ako B, ak A = 1 a B = 0. Podľa toho je B väčšie ako A, ak B = 1 a A = 0. Pravdivostná tabuľka je znázornená na obr. 5.62.
Logické funkcie sa získajú z pravdivostnej tabuľky:
X = (AaB)v(AaB);
Y = A a B;
Z = A a B.
Tieto rovnice nie sú ďalej zjednodušované Požadovaná schéma je znázornená na obr. 5.63.

Ryža. 5.62.

Ryža. 5.63.

Pred opustením továrne sa tranzistory skontrolujú, aby sa zabezpečilo, že štyri dôležité parametre A, B, C a D sú v prijateľnom rozsahu. Na meranie sa používajú štyri digitálne snímače. Snímač vydá 1, ak je nameraná hodnota v rozsahu prijateľných hodnôt. Ak je nameraná hodnota mimo rozsahu prijateľných hodnôt, snímač vydá 0.
Tranzistory sú triedené pomocou digitálneho obvodu. Ak sú všetky štyri hodnoty v rámci prijateľných hodnôt, výstupná premenná M sa stane 1. Ak je len B mimo rozsahu prijateľných hodnôt, potom výstupná premenná N bude 1. Ak sú len B a D mimo rozsahu prijateľné hodnoty, potom výstupná premenná U dostane stav 1. Vo všetkých ostatných prípadoch je výstup Z 1, čo znamená, že tranzistor je chybný.
Je potrebné vypočítať obvod a zostaviť ho iba na prvkoch NAND (nazývaných aj „na báze NAND“).
Vstupmi sú štyri premenné A, B, C a D. Výstupné premenné sú M, N, U a Z. M sa stane 1, ak A = 1, 5 = 1, C = 1 a D = 1. Toto je možnosť 16 v pravdivostná tabuľka (obr.
5,64). bude 1, ak A = \, 5 = 0, C = 1 a D = 1 (možnosť 14). U sa bude rovnať 1, ak A je 1, 5 = 0,
C = 1 a D = 0 (možnosť 6). Vo všetkých ostatných prípadoch, okrem 6, 14 a 16, Z-1.

Ryža. 5.64. Tabuľka pravdy pre obvod triedenia tranzistorov. Pre väčšiu prehľadnosť sa nuly pre výstupnú premennú nezapisujú

Výsledkom sú nasledujúce logické funkcie:
M = AaBaCaD;
N = A a B a C a D; U = A a B aC a D. Funkcia Z obsahuje 13 úplných spojok. Z je potom vždy 1, ak sa ani M, N, ani U nerovná 1. Pre Z je lepšie písať normálny tvar OR (pozri obr. 5.64):
Z = (^4a5aCaD)v^a5aCaD^v^aBaCaZ));
Z = M v N vU. Potom pre priamu hodnotu Z:
Z = M v N vU.

Ryža. 5,65.

Nájdené funkcie pre M, Nn U nie je možné zjednodušiť. Musia sa prepočítať spolu s rovnicou pre Z na základ NAND:
M = AaBaCaD\
N = A a B aC, D;
U = AlVlSlO",
Z = MvNvU = MaNaU;
Z = M a N a U.
Z týchto rovníc sa získa diagram znázornený na obr. 5,65. Prostredníctvom výstupov M, N, U a Z je možné ovládať mechanické zariadenie, ktoré rozdeľuje tranzistory do 4 rôznych kontajnerov.

Pri implementácii algoritmov spracovania analógových signálov je často potrebné vypočítať matematické funkcie. Najbežnejšie funkcie sú logaritmické a exponenciálne funkcie. Tieto funkcie sa používajú v schémach na zníženie a zvýšenie dynamického rozsahu prenášaného alebo zaznamenaného signálu (kompaning). Ďalšou bežnou aplikáciou matematických obvodov s exponentom a logaritmom je výpočet súčinu a delenia vstupných signálov.

Na výpočet nelineárnej funkcie sa často používa operačný zosilňovač obklopený negatívnou spätnou väzbou. Ako príklad je na obrázku 1 znázornený obvod logaritmického zosilňovača.

Obrázok 1. Obvod logaritmického zosilňovača

V tomto obvode je v obvode negatívnej spätnej väzby zahrnutý nelineárny prvok (polovodičová dióda), ktorý má exponenciálnu závislosť prúdu od použitého napätia. V dôsledku spätnej väzby sa závislosť výstupného napätia na vstupe stáva logaritmickou. Zosilnenie tohto logaritmického obvodu je určené R1. Logaritmický obvod je zvyčajne navrhnutý pre jednotný zisk.

Ak je v tomto obvode použitá dióda s kvadratickou prúdovo-napäťovou charakteristikou, potom vypočíta druhú odmocninu vstupného signálu. Je vhodné ho použiť v obvodoch na určenie amplitúdy signálu počas kvadratúrneho spracovania signálu.

(1),

Inverzná hodnota logaritmickej funkcie, exponenciála, sa vypočíta podobným spôsobom. Len v tomto prípade nie je nelineárny prvok zahrnutý v obvode spätnej väzby, ale na vstupe zosilňovača. Obrázok 2 znázorňuje schému na výpočet exponentu na operačnom zosilňovači.

Obrázok 2. Schéma výpočtu exponentu

Ak je v tomto obvode použitá dióda s kvadratickou charakteristikou prúd-napätie, potom obvod vypočíta druhú mocninu vstupného napätia a môže byť použitý ako obvod na určenie výkonu vstupného signálu.

Pomocou týchto obvodov na výpočet matematických funkcií môžete vypočítať súčin dvoch analógových signálov. Toto využíva známu vlastnosť logaritmov na nahradenie súčinu premenných súčtom logaritmov týchto premenných. Na inverzný prevod sa používa funkcia výpočtu exponentov. V tomto prípade je základ logaritmu úplne nepodstatný.

(2),

Multiplikačný obvod, ktorý implementuje vzorec (1) na operačných zosilňovačoch, je znázornený na obrázku 3.

Obrázok 3. Obvod multiplikátora operačného zosilňovača

Napriek jednoduchosti implementácie sa takáto schéma používa pomerne zriedkavo, pretože Násobenie je možné len pre kladné vstupné hodnoty. Preto sa zvyčajne používajú multiplikačné obvody postavené na základe.

Na výpočet funkcií nie je vždy možné vybrať nelineárny prvok s danou charakteristikou prúdového napätia. V tomto prípade môžete použiť po častiach lineárnu aproximáciu funkcie. Je ľahké implementovať akýkoľvek zisk na operačnom zosilňovači jednoduchou zmenou hodnoty odporu v obvode spätnej väzby, čím sa nastaví strmosť funkcie. Prepínanie odporov pri zmene vstupného napätia je najjednoduchšie vykonať pomocou diódových spínačov, ktoré sú napájané nami nastaveným vypínacím napätím. Podobný diagram je znázornený na obrázku 4.

Obrázok 4. Obvod funkčného zosilňovača

Na výpočet zložitejších funkcií sa často používajú multiplikátory založené na tranzistoroch. V najjednoduchšom prípade môžu byť vstupy X a Y kombinované, aby sa získal obvod na výpočet druhej mocniny vstupného signálu ( Y=X 2).

Môžu byť použité ako elektronické regulátory napätia. Privedením konštantného napätia na jeden zo vstupov môžete regulovať úroveň striedavého napätia dodávaného na výstup na výstupe.

Literatúra:

Spolu s článkom „Schémy na výpočet matematických funkcií“ čítajte:

2.1 Vývoj algoritmu.

Algoritmus- Toto

a. opis postupnosti činností na vyriešenie problému alebo dosiahnutie cieľa;

b. pravidlá pre vykonávanie základných operácií spracovania údajov;

c. popis výpočtov pomocou matematických vzorcov.

Pred začatím vývoja algoritmu je potrebné jasne pochopiť úlohu: čo je potrebné získať ako výsledok, aké počiatočné údaje sú potrebné a čo je k dispozícii, aké obmedzenia existujú pre tieto údaje. Ďalej si musíte zapísať, aké kroky je potrebné vykonať, aby ste získali požadovaný výsledok z počiatočných údajov.

V praxi sú najbežnejšie formy prezentovania algoritmov:

Verbálne (nahrávky v prirodzenom jazyku);

Grafika (obrázky z grafických symbolov);

Pseudokódy (poloformalizované popisy algoritmov v podmienenom algoritmickom jazyku, vrátane prvkov programovacieho jazyka a fráz v prirodzenom jazyku, všeobecne akceptované matematické zápisy atď.);

Programovanie (texty v programovacích jazykoch).

Verbálny spôsob zápisu algoritmov je popisom po sebe nasledujúcich fáz spracovania údajov. Algoritmus je špecifikovaný vo voľnej forme v prirodzenom jazyku.

Príklad. Napíšte algoritmus na nájdenie najväčšieho spoločného deliteľa (GCD) dvoch prirodzených čísel.

Algoritmus môže byť nasledovný:

1. nastaviť dve čísla;

2. ak sú čísla rovnaké, potom vezmite ktorékoľvek z nich ako odpoveď a zastavte sa, inak pokračujte vo vykonávaní algoritmu;

3. určiť najväčšie z čísel;

4. nahraďte väčšie číslo rozdielom medzi väčším a menším číslom;

5. zopakujte algoritmus z kroku 2.

Opísaný algoritmus je použiteľný pre akékoľvek prirodzené čísla a mal by viesť k riešeniu problému. Presvedčte sa o tom pomocou tohto algoritmu na určenie najväčšieho spoločného deliteľa čísel 125 a 75.

Verbálna metóda nie je rozšírená z nasledujúcich dôvodov:

Takéto opisy nie sú striktne formalizovateľné;

Trpieť rozvláčnosťou poznámok;

Pri výklade jednotlivých predpisov je priestor na nejednoznačnosť.

Grafický spôsob prezentácie algoritmov je kompaktnejší a názornejší v porovnaní s verbálnym.

Pri grafickom znázornení je algoritmus znázornený ako postupnosť vzájomne prepojených funkčných blokov, z ktorých každý zodpovedá vykonaniu jednej alebo viacerých akcií.

Toto grafické znázornenie sa nazýva vývojový diagram alebo vývojový diagram.

Pseudokód je systém zápisov a pravidiel navrhnutých na jednotné zapisovanie algoritmov.

Zaberá medziľahlé miesto medzi prirodzenými a formálnymi jazykmi.

Na jednej strane je blízky bežnému prirodzenému jazyku, takže algoritmy sa v ňom dajú písať a čítať ako bežný text. Na druhej strane pseudokód používa niektoré formálne konštrukcie a matematickú symboliku, čím sa zápis algoritmu približuje všeobecne akceptovanej matematickej notácii.

V pseudokóde nie sú prijaté prísne syntaktické pravidlá pre písanie príkazov, ktoré sú vlastné formálnym jazykom, čo uľahčuje písanie algoritmu vo fáze návrhu a umožňuje použiť širšiu sadu príkazov určených pre abstraktného vykonávateľa. Pseudokód však zvyčajne obsahuje niektoré konštrukcie, ktoré sú vlastné formálnym jazykom, čo uľahčuje prechod od písania v pseudokóde k písaniu algoritmu vo formálnom jazyku. Najmä v pseudokóde, ako aj vo formálnych jazykoch existujú funkčné slová, ktorých význam je určený raz a navždy. Neexistuje žiadna jednotná alebo formálna definícia pseudokódu, takže sú možné rôzne pseudokódy, ktoré sa líšia množinou funkčných slov a základných (základných) konštrukcií.

2.2 Bloková schéma.

Vývojový diagram je grafické znázornenie algoritmu, v ktorom je znázornený ako postupnosť vzájomne prepojených funkčných blokov, z ktorých každý zodpovedá vykonaniu jednej alebo viacerých akcií.

Vo vývojovom diagrame každý typ akcie (zadávanie počiatočných údajov, výpočet hodnôt výrazov, kontrola podmienok, riadenie opakovania akcií, dokončenie spracovania atď.) zodpovedá geometrickému útvaru reprezentovanému ako symbol bloku. Symboly blokov sú spojené prechodovými čiarami, ktoré určujú poradie vykonávania akcií.

Tu sú najčastejšie používané symboly.

Názov symbolu	Označenie a príklad plnenia	Vysvetlenie
Proces		Výpočtová akcia alebo postupnosť akcií
Riešenie		Kontrola podmienok
Modifikácia		Začiatok cyklu
Preddefinovaný proces		Výpočty podľa podprogramu, štandardného podprogramu
Vstup výstup		I/O vo všeobecnosti
Štart stop		Začiatok, koniec algoritmu, vstup a výstup do podprogramu
Dokument		Výsledky tlače

Blok „proces“ sa používa na označenie akcie alebo postupnosti akcií, ktoré menia význam, formu prezentácie alebo umiestnenie údajov. Na zlepšenie prehľadnosti diagramu je možné spojiť niekoľko jednotlivých blokov spracovania do jedného bloku. Prezentácia jednotlivých operácií je celkom voľná.

Blok "rozhodnutie" sa používa na označenie prechodov podmieneného riadenia. Každý blok „riešenia“ musí identifikovať otázku, podmienku alebo porovnanie, ktoré definuje.

Blok "modifikácie" sa používa na organizáciu cyklických štruktúr. (Slovo modifikácia znamená modifikáciu, premenu). Vo vnútri bloku je zapísaný parameter cyklu, pre ktorý je pri každom opakovaní uvedená jeho počiatočná hodnota, okrajová podmienka a krok zmeny hodnoty parametra.

Blok "preddefinovaný proces" sa používa na označenie volaní pomocných algoritmov, ktoré existujú autonómne vo forme nejakých nezávislých modulov, a na volania knižničných rutín.

Príklad. Zostavte blokovú schému algoritmu na určenie výšok ha, hb, hc trojuholníka so stranami a, b, c, ak

Kde p = (a + b + c) / 2.
Riešenie. Predstavme si notáciu potom h a = t/a, h b = t/b, h c = t/c. Vývojový diagram musí obsahovať začiatok, vstup a, b, c, výpočet p, t, h a, h b, h c , vypíšte výsledky a zastavte.

2.3 Štruktúry algoritmov.

Algoritmy si možno predstaviť ako určité štruktúry pozostávajúce z jednotlivých základných (t. j. základných) prvkov. Prirodzene, s týmto prístupom k algoritmom by štúdium základných princípov ich návrhu malo začať štúdiom týchto základných prvkov.

Logická štruktúra každého algoritmu môže byť reprezentovaná kombináciou troch základných štruktúr: nasledujúca, vetviaca a slučková.

Charakteristickým znakom základných štruktúr je prítomnosť jedného vstupu a jedného výstupu.

1. Nasleduje základná štruktúra. Vytvorené zo sledu akcií, ktoré nasledujú po sebe:

2. Základná štruktúra vetvenia. Poskytuje v závislosti od výsledku kontroly stavu (áno alebo nie) výber jedného z alternatívnych spôsobov fungovania algoritmu. Každá cesta vedie k spoločnému výstupu, takže algoritmus bude pokračovať v činnosti bez ohľadu na to, ktorá cesta je zvolená.

Štruktúra vetvenia existuje v štyroch hlavných variantoch:

Ak-tak-inak;

Výber je iný.

1) if-if podmienka then action end if 2) if-else if podmienka potom akcie 1 inak akcie 2 skončia, ak 3) voľba voľby s podmienkou 1: akcie 1 s podmienkou 2: akcie 2. . . . . . . . . . . . pod podmienkou N: akcie N koniec voľby 4) voľba - inak voľba za podmienky 1: akcia 1 za podmienky 2: akcia 2. . . . . . . . . . . . pod podmienkou N: akcie N inak akcie N+1 koniec voľby

Príklad. Vytvorte blokovú schému algoritmu na výpočet funkcie

Základnou štruktúrou je cyklus. Poskytuje opakované vykonávanie určitého súboru akcií, ktoré sa nazývajú telo slučky.

Štruktúra cyklu existuje v troch hlavných verziách:

Typ slučky Pre.

Dáva pokyn na vykonanie tela slučky pre všetky hodnoty určitej premennej (parametra slučky) v danom rozsahu.

Typ slučky Zbohom.

Prikáže vykonať telo cyklu, pokiaľ je splnená podmienka napísaná za slovom while.

Typ slučky robiť, kým.

Prikáže vykonať telo cyklu, pokiaľ je splnená podmienka napísaná za slovom while. Podmienka sa skontroluje po vykonaní tela slučky.

Všimnite si, že slučky for a while sa tiež nazývajú slučky s predbežnou kontrolou podmienky a slučky na vykonanie - while - slučky s následnou kontrolou podmienky. Inými slovami, telá cyklov for a while sa nemusia vykonať ani raz, ak podmienka ukončenia cyklu nie je na začiatku pravdivá. Robte telo cyklu, kým sa nevykoná aspoň raz, aj keď podmienka na ukončenie cyklu nie je spočiatku pravdivá.

Cyklus pre i od i1 do i2 krok i3 telo cyklu (postupnosť akcií) koniec cyklu loop while condition loop telo (sekvencia akcií) koniec cyklu telo cyklu do cyklu (postupnosť akcií) až do konca cyklu

s danou presnosťou (pre daný striedavý výkonový rad sa požadovaná presnosť dosiahne, keď sa ďalší člen v absolútnej hodnote zmenší).

Počítanie súm je typická cyklická úloha. Zvláštnosťou nášho špecifického problému je, že počet termínov (a následne aj počet opakovaní tela slučky) je vopred neznámy. Preto sa slučka musí skončiť, keď sa dosiahne požadovaná presnosť.

Pri zostavovaní algoritmu je potrebné vziať do úvahy, že znamienka pojmov sa striedajú a zvyšuje sa mocnosť čísla x v čitateloch pojmov.

Vyriešte tento problém priamo výpočtom čiastkového súčtu v každom i-tom kroku

S:=S+(-1)**(i-1)*x**i/i,

skončíme s veľmi neefektívnym algoritmom, ktorý si vyžaduje veľké množstvo operácií. Je oveľa lepšie usporiadať výpočty nasledovne: ak označíte čitateľa ľubovoľného termínu písmenom p, potom sa čitateľ nasledujúceho termínu bude rovnať -р*х (znamienko mínus zaisťuje striedanie znamienok termíny) a samotný termín bude m

sa bude rovnať p/i, kde i je číslo termínu.

Algoritmus, ktorý obsahuje iteračnú slučku, sa nazýva iteračný algoritmus. Iteračné algoritmy sa používajú pri implementácii iteračných numerických metód. V iteračných algoritmoch je potrebné zabezpečiť splnenie podmienky pre ukončenie cyklu (konvergencia iteračného procesu). V opačnom prípade sa algoritmus zacyklí, t.j. hlavná vlastnosť algoritmu - účinnosť - nebude splnená.

Vnorené slučky.

Môžu nastať prípady, keď je potrebné zopakovať určitú postupnosť príkazov v tele cyklu, teda zorganizovať vnútornú slučku. Táto štruktúra sa nazýva slučka v rámci slučky alebo vnorené slučky. Hĺbka vnorenia slučiek (to znamená počet slučiek vnorených do seba) môže byť rôzna.

Pri použití takejto štruktúry je pre úsporu času počítača potrebné presunúť všetky príkazy, ktoré nezávisia od parametra vnútornej slučky, z vnútornej slučky do vonkajšej.

Príklad vnorené slučky pre. Vypočítajte súčet prvkov danej matice A(5,3).

Príklad zatiaľ vnorené slučky. Vypočítajte súčin tých prvkov danej matice A(10,10), ktoré sa nachádzajú na priesečníku párnych riadkov a párnych stĺpcov.