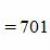Überlagerung von Funktionen (komplexe Funktion). Funktionsdefinition Selbstduale boolesche Funktionen

Korrespondenz G zwischen Mengen A Und IN eine Teilmenge genannt. Wenn, dann sagen sie das B

entspricht A. Die Menge aller entsprechenden Elemente

Angerufen Weg Element a. Die Menge aller, denen das Element entspricht, wird aufgerufen

Prototyp Element B.

Viele Paare (b, a) so etwas, das man invers nennt

in Richtung G und wird bezeichnet. Die Konzepte von Bild und Prototyp für

"G und sind zueinander invers.

Beispiele. 1) Vergleichen wir es mit einer natürlichen Zahl P

Menge reeller Zahlen . Bild der Nummer 5

Es wird eine halbe Pause geben

(Dies bedeutet die größte ganze Zahl, kleiner oder gleich X). Der Prototyp der Zahl 5 in dieser Korrespondenz ist eine unendliche Menge: Halbintervall.

In Bezug auf den Abschluss können wir andere Definitionen von Abschluss und Vollständigkeit angeben (äquivalent zu den ursprünglichen):

K ist eine abgeschlossene Klasse, wenn K = [K];

K ist ein vollständiges System, wenn [K] = P 2 .

Beispiele.

* (0), (1) – geschlossene Klassen.

* Eine Menge von Funktionen einer Variablen ist eine geschlossene Klasse.

* - geschlossene Klasse.

* Klasse (1, x+y) ist keine geschlossene Klasse.

Schauen wir uns einige der wichtigsten geschlossenen Klassen an.

1. T 0- Klasse von Funktionen, die 0 bewahren.

Bezeichnen wir mit T 0 die Klasse aller Funktionen der Algebra der Logik f(x 1 , x 2 , ... , x n) unter Beibehaltung der Konstante 0, also Funktionen, für die f(0, ... , 0 ) = 0.

Es ist leicht zu erkennen, dass es Funktionen gibt, die zu T 0 gehören, und Funktionen, die nicht zu dieser Klasse gehören:

0, x, xy, xÚy, x+y О T 0 ;

Aus der Tatsache, dass Ï T 0 ist, folgt beispielsweise, dass es nicht durch Disjunktion und Konjunktion ausgedrückt werden kann.

Da die Tabelle für die Funktion f aus der Klasse T 0 in der ersten Zeile den Wert 0 enthält, können Sie für Funktionen aus T 0 beliebige Werte nur auf 2 n - 1 Satz Variablenwerte setzen, das heißt

,

Dabei ist die Menge der Funktionen, die 0 bewahren und von n Variablen abhängen.

Zeigen wir, dass T 0 eine abgeschlossene Klasse ist. Da xÎT 0 , reicht es zur Begründung der Geschlossenheit aus, die Geschlossenheit in Bezug auf die Operation der Überlagerung zu zeigen, da die Operation der Änderung von Variablen ein Sonderfall der Überlagerung mit der Funktion x ist.

Lassen . Dann genügt es, das zu zeigen. Letzteres ergibt sich aus der Gleichheitskette

2. T 1- Klasse von Funktionen, die 1 erhalten.

Bezeichnen wir mit T 1 die Klasse aller Funktionen der Algebra der Logik f(x 1, x 2, ... , x n) unter Beibehaltung der Konstante 1, also Funktionen, für die f(1, ... , 1 ) = 1.

Es ist leicht zu erkennen, dass es Funktionen gibt, die zu T 1 gehören, und Funktionen, die nicht zu dieser Klasse gehören:

1, x, xy, xÚy, xºy О T 1 ;

0, , x+y Ï T 1 .

Aus der Tatsache, dass x + y Ï T 0 ist, folgt beispielsweise, dass x + y nicht durch Disjunktion und Konjunktion ausgedrückt werden kann.

Die Ergebnisse über die Klasse T 0 werden trivial auf die Klasse T 1 übertragen. Somit haben wir:

T 1 - geschlossene Klasse;

.

3. L- Klasse linearer Funktionen.

Bezeichnen wir mit L die Klasse aller Funktionen der Algebra der Logik f(x 1 , x 2 , ... , x n), die linear sind:

Es ist leicht zu erkennen, dass es Funktionen gibt, die zu L gehören, und Funktionen, die nicht zu dieser Klasse gehören:

0, 1, x, x+y, x 1 º x 2 = x 1 + x 2 + 1, = x+1 О L;

Beweisen wir zum Beispiel, dass xÚy Ï L .

Nehmen wir das Gegenteil an. Wir suchen nach einem Ausdruck für xÚy in Form einer linearen Funktion mit unbestimmten Koeffizienten:

Für x = y = 0 gilt a=0,

für x = 1, y = 0 gilt b = 1,

für x = 0, y = 1 gilt g = 1,

aber dann gilt für x = 1, y = 1 1v 1 ¹ 1 + 1, was die Nichtlinearität der Funktion xy beweist.

Der Beweis der Abgeschlossenheit der Klasse linearer Funktionen ist recht offensichtlich.

Da eine lineare Funktion durch die Angabe der Werte n+1 des Koeffizienten a 0 , ... , a n eindeutig bestimmt wird, ist die Anzahl der linearen Funktionen in der Klasse L (n) von Funktionen abhängig von n Variablen gleich 2 n+1 .

.

4.S- Klasse selbstdueller Funktionen.

Die Definition der Klasse der selbstdualen Funktionen basiert auf der Verwendung des sogenannten Prinzips der Dualität und der dualen Funktionen.

Die durch die Gleichheit definierte Funktion wird aufgerufen dual zur Funktion .

Offensichtlich wird die Tabelle für die Dualfunktion (mit der Standardreihenfolge der Sätze von Variablenwerten) aus der Tabelle für die ursprüngliche Funktion erhalten, indem die Spalte der Funktionswerte invertiert (d. h. 0 durch 1 und 1 durch 0 ersetzt) ​​wird und es umdrehen.

Das ist leicht zu erkennen

(x 1 Ú x 2)* = x 1 Ù x 2 ,

(x 1 Ù x 2)* = x 1 Ú x 2 .

Aus der Definition folgt, dass (f*)* = f, d. h. die Funktion f ist dual zu f*.

Lassen Sie eine Funktion durch Superposition durch andere Funktionen ausgedrückt werden. Die Frage ist, wie man eine Formel erstellt, die implementiert? Bezeichnen wir mit = (x 1, ..., x n) alle verschiedenen Variablensymbole, die in den Mengen vorkommen.

Satz 2.6. Wenn die Funktion j als Überlagerung der Funktionen f, f 1, f 2, ..., f m erhalten wird, das heißt

Eine zu einer Superposition duale Funktion ist eine Superposition von Dualfunktionen.

Nachweisen.

j*(x 1 ,...,x n) = ` f(`x 1 ,...,`x n) =

Der Satz ist bewiesen. ð

Das Dualitätsprinzip folgt aus dem Satz: Wenn eine Formel A die Funktion f(x 1 , ... , x n) realisiert, dann realisiert die aus A erhaltene Formel durch Ersetzen der darin enthaltenen Funktionen durch ihre dualen Funktionen die duale Funktion f *(x 1 , ... , xn).

Bezeichnen wir mit S die Klasse aller selbstdualen Funktionen aus P 2:

S = (f | f* = f )

Es ist leicht zu erkennen, dass es Funktionen gibt, die zu S gehören, und Funktionen, die nicht zu dieser Klasse gehören:

0, 1, xy, xÚy Ï S .

Ein weniger triviales Beispiel für eine selbstduale Funktion ist die Funktion

h(x, y, z) = xy Ú xz Ú ​​\u200b\u200byz;

Mit dem Satz über die zur Überlagerung duale Funktion haben wir

h*(x, y, z)= (x Ú y)Ù(x Ú z) Ù (y Ù z) = x y Ú x z Ú y z; h = h* ; h О S.

Für eine selbstduale Funktion gilt die Identität

also auf Sets und , was wir Gegenteil nennen werden, nimmt die Selbstdualfunktion entgegengesetzte Werte an. Daraus folgt, dass die Selbstdualfunktion vollständig durch ihre Werte in der ersten Hälfte der Zeilen der Standardtabelle bestimmt wird. Daher ist die Anzahl der selbstdualen Funktionen in der Klasse S (n) von Funktionen abhängig von n Variablen gleich:

.

Beweisen wir nun, dass die Klasse S abgeschlossen ist. Da xÎS , reicht es zur Rechtfertigung der Geschlossenheit aus, die Geschlossenheit in Bezug auf die Operation der Überlagerung zu zeigen, da die Operation der Änderung von Variablen ein Sonderfall der Überlagerung mit der Funktion x ist. Lassen . Dann genügt es, das zu zeigen. Letzteres wird direkt installiert:

5. M- Klasse monotoner Funktionen.

Bevor das Konzept einer monotonen Funktion in der Algebra der Logik definiert wird, ist es notwendig, eine Ordnungsbeziehung für die Menge ihrer Variablen einzuführen.

Man sagt, dass Set vor Set kommt (oder „nicht mehr als“ oder „kleiner als oder gleich“) und verwenden Sie die Notation if a i £ b i für alle i = 1, ... , n. Wenn und , dann sagen wir, dass die Menge strikt vor der Menge liegt (oder „strikt kleiner“ oder „kleiner als“ die Menge) und verwenden die Notation . Mengen und heißen vergleichbar, wenn entweder , oder . Falls keine dieser Beziehungen zutrifft, heißen die Mengen und unvergleichbar. Beispielsweise ist (0, 1, 0, 1) £ (1, 1, 0, 1), aber die Mengen (0, 1, 1, 0) und (1, 0, 1, 0) sind nicht vergleichbar. Somit ist die Relation £ (oft als Präzedenzrelation bezeichnet) eine Teilordnung auf der Menge B n. Nachfolgend finden Sie Diagramme der teilweise geordneten Mengen B 2, B 3 und B 4.

Die eingeführte partielle Ordnungsrelation ist ein äußerst wichtiges Konzept, das weit über den Rahmen unseres Kurses hinausgeht.

Jetzt haben wir die Möglichkeit, den Begriff einer monotonen Funktion zu definieren.

Die Funktion der logischen Algebra wird aufgerufen eintönig, wenn für zwei beliebige Mengen und , so dass die Ungleichung gilt . Die Menge aller monotonen Funktionen der Algebra der Logik wird mit M bezeichnet, und die Menge aller monotonen Funktionen in Abhängigkeit von n Variablen wird mit M(n) bezeichnet.

Es ist leicht zu erkennen, dass es Funktionen gibt, die zu M gehören, und Funktionen, die nicht zu dieser Klasse gehören:

0, 1, x, xy, xÚy О M;

x+y, x®y, xºy Ï M .

Zeigen wir, dass die Klasse der monotonen Funktionen M eine abgeschlossene Klasse ist. Da xОМ, reicht es zur Rechtfertigung der Geschlossenheit aus, die Geschlossenheit in Bezug auf die Operation der Überlagerung zu zeigen, da die Operation der Änderung von Variablen ein Sonderfall der Überlagerung mit der Funktion x ist.

Lassen . Dann genügt es, das zu zeigen.

Es seien Mengen von Variablen bzw. Funktionen j, f 1 , ... , f m , und die Menge der Variablen der Funktion j besteht aus genau diesen Variablen, die in den Funktionen f 1 , ... , f m vorkommen. Seien und seien zwei Wertemengen der Variablen, und . Diese Mengen definieren die Mengen variable Werte , so dass . Aufgrund der Monotonie der Funktionen f 1 , ... , f m

und aufgrund der Monotonie der Funktion f

Von hier aus bekommen wir

Die Anzahl der von n Variablen abhängigen monotonen Funktionen ist nicht genau bekannt. Die Untergrenze lässt sich leicht ermitteln:

wobei - der ganzzahlige Teil von n/2 ist.

Es stellt sich auch heraus, dass die Schätzung von oben einfach zu hoch ist:

Die Verfeinerung dieser Schätzungen ist eine wichtige und interessante Aufgabe der modernen Forschung.

Vollständigkeitskriterium

Nun sind wir in der Lage, ein Vollständigkeitskriterium (Satz von Post) zu formulieren und zu beweisen, das die notwendigen und hinreichenden Bedingungen für die Vollständigkeit eines Systems von Funktionen bestimmt. Lassen Sie uns der Formulierung und dem Beweis des Vollständigkeitskriteriums mehrere notwendige Lemmata voranstellen, die von unabhängigem Interesse sind.

Lemma 2.7. Lemma über nicht-selbst-duale Funktion.

Wenn f(x 1 , ... , x n)Ï S , dann kann daraus durch Einsetzen der Funktionen x und `x eine Konstante erhalten werden.

Nachweisen. Da fÏS, dann gibt es eine Menge von Werten der Variablen
=(a 1 ,...,a n) so dass

f(`a 1 ,...,`a n) = f(a 1 ,...,a n)

Ersetzen wir die Argumente in der Funktion f:

x i wird ersetzt durch ,

das heißt, lassen Sie uns die Funktion formulieren und betrachten

Somit haben wir eine Konstante erhalten (obwohl nicht bekannt ist, um welche Konstante es sich handelt: 0 oder 1). ð

Lemma 2.8. Lemma über nichtmonotone Funktionen.

Wenn die Funktion f(x 1 ,...,x n) nicht monoton ist, f(x 1 ,...,x n) Ï M, dann kann daraus eine Negation erhalten werden, indem Variablen geändert und die Konstanten 0 und ersetzt werden 1.

Nachweisen. Da f(x 1 ,...,x n) Ï M, dann gibt es Wertemengen seiner Variablen, , , so dass und für mindestens einen Wert i, a i< b i . Выполним следующую замену переменных функции f:

x i werde ersetzt durch

Nach einer solchen Substitution erhalten wir eine Funktion einer Variablen j(x), für die gilt:

Das bedeutet, dass j(x)=`x. Das Lemma ist bewiesen. ð

Lemma 2.9. Lemma über nichtlineare Funktionen.

Wenn f(x 1 ,...,x n) Ï L , dann können wir daraus durch Ersetzen der Konstanten 0, 1 und Verwendung der Funktion `x die Funktion x 1 &x 2 erhalten.

Nachweisen. Stellen wir f als DNF dar (zum Beispiel als perfektes DNF) und verwenden wir die Beziehungen:

Beispiel. Lassen Sie uns zwei Beispiele für die Anwendung dieser Transformationen geben.

Somit wird eine in disjunktiver Normalform geschriebene Funktion nach Anwendung der angegebenen Beziehungen, dem Öffnen von Klammern und einfachen algebraischen Transformationen zu einem Mod-2-Polynom (Zhegalkin-Polynom):

wobei A 0 eine Konstante und A i eine Konjunktion einiger Variablen aus der Zahl x 1,..., x n, i = 1, 2, ..., r ist.

Wenn jede Konjunktion A i nur aus einer Variablen besteht, dann ist f eine lineare Funktion, was der Bedingung des Lemmas widerspricht.

Folglich gibt es im Zhegalkin-Polynom für die Funktion f einen Term, der mindestens zwei Faktoren enthält. Ohne Beschränkung der Allgemeinheit können wir davon ausgehen, dass es unter diesen Faktoren Variablen x 1 und x 2 gibt. Dann lässt sich das Polynom wie folgt transformieren:

f = x 1 x 2 f 1 (x 3 ,..., x n) + x 1 f 2 (x 3 ,..., x n) + x 2 f 3 (x 3 ,..., x n) + f 4 (x 3 ,..., x n),

wobei f 1 (x 3 ,..., x n) ¹ 0 (ansonsten enthält das Polynom keine Konjunktion, die die Konjunktion x 1 x 2 enthält).

Sei (a 3 ,...,a n) so, dass f 1 (a 3 ,...,a n) = 1. Dann

j(x 1 ,x 2) = f(x 1 ,x 2 , a 3 ,...,a n) = x 1 x 2 +ax 1 +bx 2 +g ,

wobei a, b, g Konstanten gleich 0 oder 1 sind.

Lassen Sie uns die Negationsoperation verwenden, die wir haben, und betrachten wir die aus j(x 1 ,x 2) erhaltene Funktion y(x 1 ,x 2) wie folgt:

y(x 1 ,x 2) = j(x 1 +b, x 2 +a)+ab+g.

Es ist klar, dass

y(x 1 ,x 2) =(x 1 +b)(x 2 +a)+a(x 1 +b)+b(x 2 +a)+g+ab+g = x 1 x 2.

Somit,

y(x 1 ,x 2) = x 1 x 2 .

Das Lemma ist vollständig bewiesen. ð

Lemma 2.10. Das Hauptlemma des Vollständigkeitskriteriums.

Wenn die Klasse F=( f ) logischer Algebrafunktionen Funktionen enthält, die die Einheit nicht bewahren, die 0 nicht bewahren, nicht selbstdual und nicht monoton sind:

dann kann man aus den Funktionen dieses Systems durch Superpositions- und Ersetzungsoperationen von Variablen die Konstanten 0, 1 und die Funktion erhalten.

Nachweisen. Betrachten wir die Funktion. Dann

.

Es gibt zwei mögliche Fälle von Folgebetrachtungen, die in der folgenden Darstellung mit 1) und 2) bezeichnet werden.

1). Die Funktion auf der eingestellten Einheit nimmt den Wert 0 an:

.

Ersetzen wir alle Variablen der Funktion durch die Variable x. Dann die Funktion

es gibt, weil

Und .

Nehmen wir eine nicht-selbst-duale Funktion. Da wir die Funktion bereits erhalten haben, verwenden wir das Lemma für eine nicht-selbstduale Funktion (Lemma 2.7. ) können Sie daraus eine Konstante erhalten. Die zweite Konstante kann mithilfe der Funktion aus der ersten ermittelt werden. Im ersten betrachteten Fall werden also Konstanten und Negation erhalten. . Der zweite Fall und damit das Hauptlemma des Vollständigkeitskriteriums sind vollständig bewiesen. ð

Satz 2.11. Ein Kriterium für die Vollständigkeit von Funktionensystemen in der Algebra der Logik (Satz von Post).

Damit das Funktionensystem F = (f i) vollständig ist, ist es notwendig und ausreichend, dass es in keiner der fünf abgeschlossenen Klassen T 0, T 1, L, S, M vollständig enthalten ist, also z In jeder der Klassen T 0 , T 1 , L , S, M in F gibt es mindestens eine Funktion, die nicht zu dieser Klasse gehört.

Notwendigkeit. Sei F ein vollständiges System. Nehmen wir an, dass F in einer der angegebenen Klassen enthalten ist, bezeichnen wir es mit K, d.h. F Í K. Die letzte Inklusion ist unmöglich, da K eine geschlossene Klasse ist, die kein vollständiges System ist.

Angemessenheit. Das gesamte Funktionensystem F = (f i ) sei in keiner der fünf abgeschlossenen Klassen T 0 , T 1 , L , S , M enthalten. Nehmen wir die folgenden Funktionen in F:

Basierend auf dem Hauptlemma (Lemma 2.10 ) Aus einer Funktion, die 0 nicht bewahrt, einer Funktion, die 1 nicht bewahrt, nicht selbstdualen und nicht monotonen Funktionen kann man die Konstanten 0, 1 und die Negationsfunktion erhalten:

.

Basierend auf dem Lemma zu nichtlinearen Funktionen (Lemma 2.9 ) aus Konstanten, Negation und einer nichtlinearen Funktion können wir die Konjunktion erhalten:

.

Funktionssystem - ein vollständiges System gemäß dem Satz über die Möglichkeit, jede Funktion der Algebra der Logik in Form einer perfekten disjunktiven Normalform darzustellen (beachten Sie, dass Disjunktion durch Konjunktion und Negation in der Form ausgedrückt werden kann). ).

Der Satz ist vollständig bewiesen. ð

Beispiele.

1. Zeigen wir, dass die Funktion f(x,y) = x|y ein vollständiges System bildet. Erstellen wir eine Wertetabelle der Funktion x½y:

X	j	x|y

f(0,0) = 1, also x | yÏT 0 .

f(1,1) = 0, also x | yÏT 1 .

f(0,0) = 1, f(1,1) = 0, also x | YÏM.

f(0,1) = f(1,0) = 1, - auf gegenüberliegenden Mengen x | y nimmt die gleichen Werte an, also x | YÏS.

Was bedeutet schließlich die Nichtlinearität der Funktion?
x | j.

Basierend auf dem Vollständigkeitskriterium können wir sagen, dass f(x,y) = x | y bildet ein vollständiges System. ð

2. Zeigen wir, dass das System der Funktionen bildet ein Gesamtsystem.

Wirklich, .

So fanden wir unter den Funktionen unseres Systems: eine Funktion, die 0 nicht bewahrt, eine Funktion, die 1 nicht bewahrt, nicht-selbstduale, nicht-monotone und nichtlineare Funktionen. Basierend auf dem Kriterium der Vollständigkeit kann argumentiert werden, dass das System Funktionen hat bildet ein Gesamtsystem. ð

Daher sind wir davon überzeugt, dass das Vollständigkeitskriterium eine konstruktive und effektive Möglichkeit bietet, die Vollständigkeit von Funktionensystemen in der Algebra der Logik zu bestimmen.

Formulieren wir nun drei Folgerungen aus dem Vollständigkeitskriterium.

Folgerung 1. Jede geschlossene Klasse K von Funktionen der Algebra der Logik, die nicht mit der gesamten Menge von Funktionen der Algebra der Logik (K¹P 2) übereinstimmt, ist in mindestens einer der konstruierten geschlossenen Klassen enthalten.

Definition. Die abgeschlossene Klasse K heißt vorvoll, wenn K unvollständig ist und für jede Funktion fÏ K die Klasse K È (f) vollständig ist.

Aus der Definition folgt, dass die Precomplete-Klasse geschlossen ist.

Folgerung 2. In der Algebra der Logik gibt es nur fünf vorvollständige Klassen, nämlich: T 0, T 1, L, M, S.

Um die Folgerung zu beweisen, müssen Sie lediglich überprüfen, ob keine dieser Klassen in der anderen enthalten ist, was beispielsweise durch die folgende Tabelle der zu verschiedenen Klassen gehörenden Funktionen bestätigt wird:

	T0	T 1	L	S	M
	+	-	+	-	+
	-	+	+	-	+
	-	-	+	+	-

Folgerung 3. Von jedem vollständigen System von Funktionen ist es möglich, ein vollständiges Subsystem zu unterscheiden, das nicht mehr als vier Funktionen enthält.

Aus dem Beweis des Vollständigkeitskriteriums folgt, dass nicht mehr als fünf Funktionen unterschieden werden können. Aus dem Beweis des Hauptlemmas (Lemma 2.10 ) folgt daraus ist entweder nicht-selbst-dual oder bewahrt nicht die Einheit und ist nicht monoton. Daher sind nicht mehr als vier Funktionen erforderlich.

Thema: „Funktion: Konzept, Zuordnungsmethoden, Hauptmerkmale.“ Umkehrfunktion. Überlagerung von Funktionen.“

Epigraph der Lektion:

„Studiere etwas und denke nicht darüber nach

gelernt - absolut nutzlos.

Über etwas nachdenken, ohne es zu studieren

vorläufiger Gedankengegenstand -

Konfuzius.

Zweck und psychologische und pädagogische Ziele des Unterrichts:

1) Allgemeines pädagogisches (normatives) Ziel: Wiederholen Sie mit den Schülern die Definition und Eigenschaften einer Funktion. Führen Sie das Konzept der Überlagerung von Funktionen ein.

2) Ziele der mathematischen Entwicklung der Schüler: Verwendung von nicht standardmäßigem pädagogischem und mathematischem Material, um die geistige Erfahrung der Schüler, die sinnvolle kognitive Struktur ihrer mathematischen Intelligenz, einschließlich der Fähigkeiten zum logisch-deduktiven und induktiven, analytischen und synthetischen reversiblen Denken, algebraischen und figurativ-grafischen Denken, weiterzuentwickeln , sinnvolle Verallgemeinerung und Konkretisierung, zu Reflexion und Selbständigkeit als metakognitive Fähigkeit der Studierenden; die Entwicklung einer Kultur des schriftlichen und mündlichen Sprechens als psychologische Mechanismen pädagogischer und mathematischer Intelligenz fortzusetzen.

3) Pädagogische Aufgaben: die persönliche Ausbildung von Schülern mit kognitivem Interesse an Mathematik, Verantwortungsbewusstsein, Pflichtbewusstsein, akademischer Unabhängigkeit und kommunikativer Fähigkeit zur Zusammenarbeit mit der Gruppe, dem Lehrer und den Klassenkameraden fortzusetzen; autogoge Fähigkeit zu wettbewerbsorientierter pädagogischer und mathematischer Aktivität, Streben nach hohen und höchsten Ergebnissen (acmeisches Motiv).

Unterrichtsart: neues Material lernen; nach dem Leitkriterium mathematischer Inhalte - eine praktische Unterrichtsstunde; nach dem Kriterium der Art der Informationsinteraktion zwischen Schülern und Lehrer – eine Lektion der Zusammenarbeit.

Unterrichtsausrüstung:

1. Bildungsliteratur:

1) Kudryavtsev der mathematischen Analyse: Lehrbuch. für Universität und Universitätsstudenten. In 3 Bänden. T. 3. – 2. Aufl., überarbeitet. und zusätzlich – M.: Höher. Schule, 1989. – 352 S. : krank.

2) Demidovich-Probleme und Übungen zur mathematischen Analyse. – 9. Aufl. – M.: Verlag „Nauka“, 1977.

2. Illustrationen.

Während des Unterrichts.

1. Bekanntgabe des Themas und des Hauptbildungsziels des Unterrichts; Förderung des Pflichtgefühls, der Verantwortung und des kognitiven Interesses der Schüler bei der Vorbereitung auf die Sitzung.

2.Wiederholung des Materials anhand von Fragen.

a) Definieren Sie eine Funktion.

Eines der grundlegenden mathematischen Konzepte ist das Konzept der Funktion. Der Begriff einer Funktion ist mit der Herstellung einer Beziehung zwischen Elementen zweier Mengen verbunden.

Gegeben seien zwei nichtleere Mengen und. Ein Match f, das jedes Element mit einem und nur einem Element übereinstimmt, wird aufgerufen Funktion und schreibt y = f(x). Sie sagen auch, dass die Funktion f zeigt an viele über viele.

https://pandia.ru/text/79/018/images/image003_18.gif" width="63" height="27">.gif" width="59" height="26"> wird aufgerufen Reihe von Bedeutungen Funktion f und wird mit E(f) bezeichnet.

b) Numerische Funktionen. Funktionsgraph. Methoden zur Angabe von Funktionen.

Die Funktion sei gegeben.

Sind die Elemente der Mengen und reelle Zahlen, dann wird die Funktion f aufgerufen numerische Funktion . Die Variable x wird aufgerufen Streit oder unabhängige Variable und y – Funktion oder abhängige Variable(von x). Was die Größen x und y selbst betrifft, so sagt man, sie seien in funktionale Abhängigkeit.

Funktionsgraph y = f(x) ist die Menge aller Punkte der Oxy-Ebene, für die x jeweils der Wert des Arguments und y der entsprechende Wert der Funktion ist.

Um die Funktion y = f(x) anzugeben, muss eine Regel angegeben werden, die es ermöglicht, bei Kenntnis von x den entsprechenden Wert von y zu finden.

Die gebräuchlichsten drei Möglichkeiten zur Angabe einer Funktion sind: analytisch, tabellarisch und grafisch.

Analytische Methode: Eine Funktion wird als eine oder mehrere Formeln oder Gleichungen angegeben.

Zum Beispiel:

Wenn der Definitionsbereich der Funktion y = f(x) nicht angegeben ist, wird angenommen, dass er mit der Menge aller Werte des Arguments übereinstimmt, für die die entsprechende Formel sinnvoll ist.

Die analytische Methode zur Angabe einer Funktion ist die fortschrittlichste, da sie Methoden der mathematischen Analyse umfasst, die es ermöglichen, die Funktion y = f(x) vollständig zu untersuchen.

Grafische Methode: Legt den Graphen der Funktion fest.

Der Vorteil einer grafischen Aufgabe ist ihre Übersichtlichkeit, der Nachteil ist ihre Ungenauigkeit.

Tabellarische Methode: Eine Funktion wird durch eine Tabelle mit einer Reihe von Argumentwerten und entsprechenden Funktionswerten angegeben. Zum Beispiel bekannte Wertetabellen trigonometrischer Funktionen, logarithmische Tabellen.

c) Hauptmerkmale der Funktion.

1. Die auf der Menge D definierte Funktion y = f(x) wird aufgerufen sogar , wenn die Bedingungen und f(-x) = f(x) erfüllt sind; seltsam , wenn die Bedingungen und f(-x) = -f(x) erfüllt sind.

Der Graph einer geraden Funktion ist symmetrisch um die Oy-Achse und eine ungerade Funktion ist symmetrisch um den Ursprung. Zum Beispiel – gerade Funktionen; und y = sinx, https://pandia.ru/text/79/018/images/image014_3.gif" width="73" height="29"> – Funktionen allgemeiner Form, d. h. weder gerade noch ungerade.

2. Die Funktion y = f(x) sei auf der Menge D definiert und sei . Wenn für irgendwelche Werte der Argumente die folgende Ungleichung folgt: , dann wird die Funktion aufgerufen zunehmend am Set; Wenn , dann wird die Funktion aufgerufen nicht abnehmend unter https://pandia.ru/text/79/018/images/image021_1.gif" width="117" height="28 src=">dann wird die Funktion aufgerufen. abnehmend An ; - nicht zunehmend .

Zunehmende, nicht zunehmende, abnehmende und nicht abnehmende Funktionen auf dem Satz https://pandia.ru/text/79/018/images/image023_0.gif" width="13" height="13">D-Wert (x +T)D und es gilt die Gleichheit f(x+T) = f(x).

Um einen Graphen einer periodischen Funktion der Periode T zu zeichnen, reicht es aus, ihn auf einem beliebigen Segment der Länge T zu zeichnen und ihn im gesamten Definitionsbereich periodisch fortzusetzen.

Beachten wir die Haupteigenschaften einer periodischen Funktion.

1) Die algebraische Summe periodischer Funktionen mit derselben Periode T ist eine periodische Funktion mit der Periode T.

2) Wenn die Funktion f(x) die Periode T hat, dann hat die Funktion f(ax) die Periode T/a.

d) Umkehrfunktion.

Sei eine Funktion y = f(x) mit einem Definitionsbereich D und einer Wertemenge E..gif" width="48" height="22"> gegeben, dann ist eine Funktion x = z(y) mit einem Definitionsbereich E und einer Wertemenge D ist definiert Eine solche Funktion heißt z(y). umkehren zur Funktion f(x) und wird in folgender Form geschrieben: . Die Funktionen y = f(x) und x = z(y) sollen zueinander invers sein. Um die Funktion x = z(y) zu finden, die zur Funktion y = f(x) invers ist, reicht es aus, die Gleichung f(x) = y nach x zu lösen.

Beispiele:

1. Für die Funktion y = 2x ist die Umkehrfunktion die Funktion x = ½ y;

2. Für die Funktion Die Umkehrfunktion ist die Funktion .

Aus der Definition einer Umkehrfunktion folgt, dass die Funktion y = f(x) genau dann eine Umkehrfunktion hat, wenn f(x) eine Eins-zu-eins-Entsprechung zwischen den Mengen D und E angibt. Daraus folgt, dass jede Eine streng monotone Funktion hat eine Umkehrung . Wenn außerdem eine Funktion zunimmt (abnimmt), erhöht (abnimmt) auch die Umkehrfunktion.

3. Neues Material studieren.

Komplexe Funktion.

Sei die Funktion y = f(u) auf der Menge D und die Funktion u = z(x) auf der Menge und für den entsprechenden Wert definiert . Dann ist auf der aufgerufenen Menge die Funktion u = f(z(x)) definiert komplexe Funktion von x (oder Überlagerung spezifizierte Funktionen, bzw Funktion von Funktion ).

Die Variable u = z(x) wird aufgerufen Zwischenargument komplexe Funktion.

Beispielsweise ist die Funktion y = sin2x eine Überlagerung zweier Funktionen y = sinu und u = 2x. Eine komplexe Funktion kann mehrere Zwischenargumente haben.

4. Mehrere Beispiele an der Tafel lösen.

5. Abschluss der Lektion.

1) theoretische und angewandte Ergebnisse des praktischen Unterrichts; differenzierte Einschätzung des geistigen Erfahrungsniveaus der Studierenden; ihr Grad der Beherrschung des Themas, ihre Kompetenz und ihre Qualität der mündlichen und schriftlichen mathematischen Rede; Grad der gezeigten Kreativität; Grad der Unabhängigkeit und Reflexion; Grad der Initiative, kognitives Interesse an einzelnen Methoden des mathematischen Denkens; Grad der Zusammenarbeit, intellektueller Wettbewerb, Wunsch nach einem hohen Maß an pädagogischer und mathematischer Aktivität usw.;

2) Bekanntgabe begründeter Noten, Unterrichtspunkte.

Build-Funktion

Wir bieten Ihnen einen Service zur Online-Erstellung von Funktionsgraphen an, an dem alle Rechte dem Unternehmen gehören Desmos. Verwenden Sie die linke Spalte, um Funktionen einzugeben. Sie können die Eingabe manuell oder über die virtuelle Tastatur am unteren Rand des Fensters vornehmen. Um das Fenster mit der Grafik zu vergrößern, können Sie sowohl die linke Spalte als auch die virtuelle Tastatur ausblenden.

Vorteile von Online-Charting

• Visuelle Anzeige der eingegebenen Funktionen
• Erstellen sehr komplexer Diagramme
• Konstruktion von implizit angegebenen Graphen (z. B. Ellipse x^2/9+y^2/16=1)
• Die Möglichkeit, Diagramme zu speichern und einen Link zu ihnen zu erhalten, der allen im Internet zur Verfügung steht
• Kontrolle von Maßstab und Linienfarbe
• Möglichkeit, Diagramme nach Punkten unter Verwendung von Konstanten zu zeichnen
• Mehrere Funktionsgraphen gleichzeitig zeichnen
• Darstellung in Polarkoordinaten (verwenden Sie r und θ(\theta))

Mit uns ist es einfach, Diagramme unterschiedlicher Komplexität online zu erstellen. Der Bau ist sofort erledigt. Gefragt ist der Dienst zum Auffinden von Schnittpunkten von Funktionen, zum Darstellen von Diagrammen, um sie zur Veranschaulichung bei der Lösung von Problemen weiter in ein Word-Dokument zu übertragen, und zum Analysieren der Verhaltensmerkmale von Funktionsdiagrammen. Der optimale Browser für die Arbeit mit Diagrammen auf dieser Website-Seite ist Google Chrome. Bei Verwendung anderer Browser kann die korrekte Funktion nicht gewährleistet werden.