2 Die logische Funktion f ist durch den Ausdruck x gegeben. Die logische Funktion F ist durch den Ausdruck gegeben

Basierend auf: Demoversionen des Einheitlichen Staatsexamens in Informatik 2015, nach dem Lehrbuch von Lyudmila Leonidovna Bosova

Im vorherigen Teil 1 haben wir mit Ihnen die logischen Operationen Disjunktion und Konjunktion besprochen. Jetzt müssen wir nur noch die Inversion analysieren und mit der Lösung der Aufgabe des Einheitlichen Staatsexamens fortfahren.

Umkehrung

Umkehrung- eine logische Operation, die jede Aussage mit einer neuen Aussage verknüpft, deren Bedeutung der ursprünglichen Aussage entgegengesetzt ist.

Die folgenden Zeichen werden zum Schreiben der Inversion verwendet: NOT, `¯`, ` ¬ `

Die Inversion wird durch die folgende Wahrheitstabelle bestimmt:

Inversion wird auch als logische Negation bezeichnet.

Jede komplexe Aussage kann in das Formular geschrieben werden logischer Ausdruck– Ausdrücke, die logische Variablen, logische Operatorzeichen und Klammern enthalten. Logische Operationen in einem logischen Ausdruck werden in der folgenden Reihenfolge ausgeführt: Umkehrung, Konjunktion, Disjunktion. Sie können die Reihenfolge der Operationen mithilfe von Klammern ändern.

Logische Operationen haben folgende Priorität: Umkehrung, Konjunktion, Disjunktion.

Und so liegt vor uns Aufgabe Nr. 2 aus dem Einheitlichen Staatsexamen in Informatik 2015

Alexandra füllte die Wahrheitstabelle für den Ausdruck F aus. Es gelang ihr nur, einen kleinen Ausschnitt der Tabelle auszufüllen:

x1	x2	x3	x4	x5	x6	x7	x8	F
	0						1	0
1			0					1
			1				1	1

Welcher Ausdruck kann F sein?

Was die Lösung des Problems erheblich erleichtert, besteht darin, dass es in jeder Version des komplexen Ausdrucks F nur eine logische Operation gibt: Multiplikation oder Addition. Im Falle einer Multiplikation /\ wenn mindestens eine Variable gleich Null ist, dann muss auch der Wert des gesamten Ausdrucks F gleich Null sein. Und im Fall der Addition V muss der Wert des gesamten Ausdrucks F gleich 1 sein, wenn mindestens eine Variable gleich eins ist.

Die in der Tabelle enthaltenen Daten für jede der 8 Variablen des Ausdrucks F reichen für uns völlig aus, um sie zu lösen.

Schauen wir uns Ausdruck Nummer 1 an:

• ? /\ 1 /\ ? /\ ? /\ ? /\ ? /\ ? /\ 0 )
• Aus der zweiten Zeile der Tabelle x1=1, x4=0 sehen wir, dass F möglich ist und gleich = 1 sein kann, wenn alle anderen Variablen gleich 1 sind (1 /\ ? /\ ? /\ 1 /\ ? /\ ? /\ ? /\ ? )
• Gemäß der dritten Zeile der Tabelle x4=1, x8=1 sehen wir, dass F=0 (? /\ ? /\ ? /\ 0 /\ ? /\ ? /\ ? /\ 0 ), und in der Tabelle haben wir F=1, und das bedeutet, dass Ausdruck Nummer eins für uns ist Definitiv nicht geeignet.

Schauen wir uns Ausdruck Nummer 2 an:

• Aus der ersten Zeile der Tabelle x2=0, x8=1 sehen wir, dass F möglich ist und gleich = 0 sein kann, wenn alle anderen Variablen gleich 0 sind (? V 0 V ? V ? V ? V ? V ? V 0 )
• Aus der zweiten Zeile der Tabelle x1=1, x4=0 sehen wir, dass F = 1 ( 1 V ? V ? V 1 V ? V ? V ? V ? )
• Gemäß der dritten Zeile der Tabelle x4=1, x8=1 sehen wir, dass F möglich ist und gleich = 1 sein kann, wenn mindestens eine der verbleibenden Variablen gleich 1 ist ( ? V ? V ? V 0 V ? V ? V ? V 0 )
  

Schauen wir uns Ausdruck Nummer 3 an:

• Aus der ersten Zeile der Tabelle x2=0, x8=1 sehen wir, dass F=0 (? /\ 0 /\ ? /\ ? /\ ? /\ ? /\ ? /\ 1 )
• Aus der zweiten Zeile der Tabelle x1=1, x4=0 sehen wir, dass F =0 (0 /\ ? /\ ? /\ 0 /\ ? /\ ? /\ ? /\ ? ), und in der Tabelle haben wir F=1, und das bedeutet, dass der Ausdruck Nummer drei uns ergibt Definitiv nicht geeignet.

Schauen wir uns Ausdruck Nummer 4 an:

• Aus der ersten Zeile der Tabelle x2=0, x8=1 sehen wir, dass F=1 ( ? V 1 V ? V ? V ? V ? V ? V 0 ), und in der Tabelle haben wir F=0, und das bedeutet, dass uns Ausdruck Nummer vier ergibt Definitiv nicht geeignet.

Bei der Lösung einer Aufgabe im Einheitlichen Staatsexamen müssen Sie genau das Gleiche tun: diejenigen Optionen verwerfen, die aufgrund der Daten in der Tabelle definitiv nicht geeignet sind. Die verbleibende mögliche Option (wie in unserem Fall Option Nummer 2) ist die richtige Antwort.

Aufgabenkatalog.
Anzahl der Programme mit Pflichtphase

Sortierung: Einfach, zuerst einfach, zuerst komplex, Beliebtheit, zuerst neu, zuerst alt
Machen Sie Tests zu diesen Aufgaben
Zurück zum Aufgabenkatalog
Version zum Drucken und Kopieren in MS Word

Performer A16 wandelt die auf dem Bildschirm angezeigte Zahl um.

Der Darsteller hat drei Teams, denen Nummern zugewiesen sind:

1. Addiere 1

2. Addiere 2

3. Mit 2 multiplizieren

Der erste von ihnen erhöht die Zahl auf dem Bildschirm um 1, der zweite erhöht sie um 2, der dritte multipliziert sie mit 2.

Ein Programm für den Darsteller A16 ist eine Folge von Befehlen.

Wie viele Programme gibt es, die die ursprüngliche Zahl 3 in die Zahl 12 umwandeln und gleichzeitig im Rechenpfad des Programms die Zahl 10 steht?

Der Berechnungsverlauf eines Programms ist eine Folge von Ergebnissen aus der Ausführung aller Programmbefehle. Für Programm 132 mit der Anfangsnummer 7 besteht die Flugbahn beispielsweise aus den Nummern 8, 16, 18.

Lösung.

Die erforderliche Anzahl an Programmen ist gleich dem Produkt aus der Anzahl der Programme, die aus der Zahl 3 die Zahl 10 erhalten, und der Zahl der Programme, die aus der Zahl 10 die Zahl 12 erhalten.

Sei R(n) die Anzahl der Programme, die die Zahl 3 in die Zahl n umwandeln, und P(n) die Anzahl der Programme, die die Zahl 10 in die Zahl n umwandeln.

Für alle n > 5 gelten folgende Beziehungen:

1. Wenn n nicht durch 2 teilbar ist, dann ist R(n) = R(n – 1) + R(n – 2), da es zwei Möglichkeiten gibt, n zu erhalten – durch Addition von eins oder Addition von zwei. Ebenso P(n) = P(n - 1) + P(n - 2)

2. Wenn n durch 2 teilbar ist, dann ist R(n) = R(n - 1) + R(n - 2) + R(n / 2). Ebenso P(n) = P(n - 1) + P(n - 2) + P(n / 2)

Berechnen wir nacheinander die Werte von R(n):

R(5) = R(4) + R(3) = 1 + 1 = 2

R(6) = R(5) + R(4) + R(3) = 2 + 1 + 1 = 4

R(7) = R(6) + R(5) = 4 + 2 = 6

R(8) = R(7) + R(6) + R(4) = 6 + 4 + 1 = 11

R(9) = R(8) + R(7) = 11 + 6 = 17

R(10) = R(9) + R(8) + R(5) = 17 + 11 + 2 = 30

Berechnen wir nun die Werte von P(n):

P(11) = P(10) = 1

P(12) = P(11) + P(10) = 2

Somit beträgt die Anzahl der Programme, die die Bedingungen des Problems erfüllen, 30 · 2 = 60.

Antwort: 60.

Antwort: 60

Quelle: Demoversion des Einheitlichen Staatsexamens 2017 in Informatik.

1. Addiere 1

2. Addiere 3

Wie viele Programme gibt es, bei denen bei gegebener Ausgangszahl 1 das Ergebnis die Zahl 17 ist und gleichzeitig in der Berechnungskurve die Zahl 9 enthalten ist? Der Berechnungsverlauf eines Programms ist eine Folge von Ergebnissen aus der Ausführung aller Programmbefehle. Für Programm 121 mit der Anfangsnummer 7 besteht die Flugbahn beispielsweise aus den Nummern 8, 11, 12.

Lösung.

Wir verwenden die Methode der dynamischen Programmierung. Erstellen wir ein Array dp, wobei dp[i] die Anzahl der Möglichkeiten ist, mit solchen Befehlen die Zahl i zu erhalten.

Dynamikbasis:

Übergangsformel:

dp[i]=dp + dp

Dabei werden die Werte für Zahlen größer als 9 nicht berücksichtigt, die aus Zahlen kleiner als 9 erhalten werden können (wodurch die Trajektorie von 9 übersprungen wird):

Antwort: 169.

Antwort: 169

Quelle: Ausbildungsarbeit in Informatik, Klasse 11, 29. November 2016, Option IN10203

Darsteller May17 rechnet die Zahl auf dem Bildschirm um.

Der Darsteller hat zwei Teams, denen Nummern zugewiesen sind:

1. Addiere 1

2. Addiere 3

Der erste Befehl erhöht die Zahl auf dem Bildschirm um 1, der zweite um 3. Das Programm für den May17-Darsteller ist eine Folge von Befehlen.

Wie viele Programme gibt es, bei denen bei gegebener Ausgangszahl 1 das Ergebnis die Zahl 15 ist und gleichzeitig in der Berechnungskurve die Zahl 8 enthalten ist? Der Berechnungsverlauf eines Programms ist eine Folge von Ergebnissen aus der Ausführung aller Programmbefehle. Für Programm 121 mit der Anfangsnummer 7 besteht die Flugbahn beispielsweise aus den Nummern 8, 11, 12.

Lösung.

Wir verwenden die Methode der dynamischen Programmierung. Erstellen wir ein Array dp, wobei dp[i] die Anzahl der Möglichkeiten ist, mit solchen Befehlen die Zahl i zu erhalten.

Dynamikbasis:

Übergangsformel:

dp[i]=dp + dp

Dies berücksichtigt jedoch keine Zahlen, die größer als 8 sind, aber wir können sie ab einem Wert unter 8 erreichen. Im Folgenden werden die Werte in den Zellen dp von 1 bis 15 angezeigt: 1 1 1 2 3 4 6 9 9 9 18 27 36 54 81 .

Jobquelle: Lösung 2437. Einheitliches Staatsexamen 2017. Informatik. V.R. Leschiner. 10 Optionen.

Aufgabe 2. Die logische Funktion F ist durch den Ausdruck gegeben. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen x, y, z entspricht.

Schreiben Sie in Ihrer Antwort die Buchstaben x, y, z in der Reihenfolge, in der ihre entsprechenden Spalten erscheinen (zuerst – der Buchstabe, der der 1. Spalte entspricht, dann – der Buchstabe, der der 2. Spalte entspricht, dann – der Buchstabe, der der 3. Spalte entspricht). Spalte) . Schreiben Sie die Buchstaben der Antwort hintereinander, es ist nicht nötig, Trennzeichen zwischen den Buchstaben zu setzen.

Lösung.

Schreiben wir den Ausdruck für F unter Berücksichtigung der Prioritäten der Operationen Negation, Konjunktion und Disjunktion um:

.

Betrachten Sie die 4. Zeile der Tabelle (1,1,0)=0. Daraus können wir erkennen, dass die dritte Stelle entweder die Variable y oder die Variable z sein muss, sonst steht in der zweiten Klammer eine 1, was zum Wert F=1 führt. Betrachten Sie nun die 5. Zeile der Tabelle (0,0,1)=1. Da x an erster oder zweiter Stelle stehen muss, ergibt die erste Klammer nur dann 1, wenn y an dritter Stelle steht. Wenn man bedenkt, dass die zweite Klammer immer gleich 0 ist, dann erhält man aufgrund der 1 in der ersten Klammer F=1. Somit haben wir festgestellt, dass y an dritter Stelle steht. Betrachten Sie abschließend die 7. Zeile der Tabelle (1,0,1)=0. Hier ist y=1 und für F=0 ist es notwendig, z=0 und x=1 zu haben, daher steht x an erster Stelle und z an zweiter Stelle.

Logikfunktion F ist durch den Ausdruck gegeben X/\ ¬y/\ (¬z\/ w).

Die Abbildung zeigt einen Ausschnitt der Wahrheitstabelle der Funktion F enthaltend Alle Mengen von Argumenten, für die die Funktion gilt F WAHR.

Bestimmen Sie die Spalte der Wahrheitstabelle der Funktion F Jede der Variablen entspricht w, X, j, z.

Schreiben Sie die Buchstaben in Ihre Antwort w, X, j, z in der Reihenfolge, in der sie kommen

ihre entsprechenden Spalten (erster – der Buchstabe, der dem ersten entspricht

Spalte; dann der Buchstabe, der der zweiten Spalte entspricht usw.) Buchstaben

Schreiben Sie Ihre Antwort in einer Reihe und setzen Sie keine Trennzeichen zwischen den Buchstaben.

nicht nötig.

Demoversion des Einheitlichen Staatsexamens USE 2017 – Aufgabe Nr. 2

Lösung:

Eine Konjunktion (logische Multiplikation) ist genau dann wahr, wenn alle Aussagen wahr sind. Daher die Variable X 1 .

Variable ¬y muss mit der Spalte übereinstimmen, in der alle Werte gleich sind 0 .

Eine Disjunktion (logische Addition) zweier Aussagen ist genau dann wahr, wenn mindestens eine Aussage wahr ist.
Disjunktion ¬z\/y z=0, w=1.

Also die Variable ¬z w entspricht der Spalte mit Variable 4 (Spalte 4).

Antwort: zyxw

Demoversion des Einheitlichen Staatsexamens USE 2016 – Aufgabe Nr. 2

Logikfunktion F wird durch den Ausdruck (¬z)/\x \/ x/\y gegeben. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen entspricht x, y, z.

Schreiben Sie in Ihrer Antwort die Buchstaben x, y, z in der Reihenfolge, in der ihre entsprechenden Spalten erscheinen (zuerst – der Buchstabe, der der 1. Spalte entspricht; dann – der Buchstabe, der der 2. Spalte entspricht; dann – der Buchstabe, der der 3. Spalte entspricht). Spalte) . Schreiben Sie die Buchstaben der Antwort hintereinander, es ist nicht nötig, Trennzeichen zwischen den Buchstaben zu setzen.

Beispiel. Gegeben sei ein Ausdruck x → y, abhängig von zwei Variablen x und y und einer Wahrheitstabelle:

Dann entspricht die 1. Spalte der Variablen y und die 2. Spalte
entspricht der Variablen x. In der Antwort müssen Sie schreiben: yx.

Lösung:

1. Schreiben wir den gegebenen Ausdruck in einfacherer Notation:

¬z*x + x*y = x*(¬z + y)

2. Konjunktion (logische Multiplikation) ist genau dann wahr, wenn alle Aussagen wahr sind. Damit also die Funktion ( F) war gleich eins ( 1 ), jeder Faktor muss gleich eins sein ( 1 ). Also wann F=1, variabel X muss mit der Spalte übereinstimmen, in der alle Werte gleich sind 1 .

3. Überlegen Sie (¬z + y), bei F=1 auch dieser Ausdruck ist gleich 1 (siehe Punkt 2).

4. Die Disjunktion (logische Addition) zweier Aussagen ist genau dann wahr, wenn mindestens eine Aussage wahr ist.
Disjunktion ¬z\/y in dieser Zeile ist nur dann wahr, wenn

1. z = 0; y = 0 oder y = 1;
2. z = 1; y = 1

5. Also die Variable ¬z entspricht Spalte mit Variable 1 (1 Spalte), Variable j

Antwort: Zyx

KIM Einheitliches Staatsexamen Einheitliches Staatsexamen 2016 (frühe Phase)– Aufgabe Nr. 2

Die logische Funktion F ist durch den Ausdruck gegeben

(x /\ y /\¬z) \/ (x /\ y /\ z) \/ (x /\¬y /\¬z).

Die Abbildung zeigt ein Fragment der Wahrheitstabelle der Funktion F, das alle Argumentmengen enthält, für die die Funktion F wahr ist. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen x, y, z entspricht.

Schreiben Sie in Ihrer Antwort die Buchstaben x, y, z in der Reihenfolge, in der ihre entsprechenden Spalten erscheinen (zuerst – der Buchstabe, der der ersten Spalte entspricht; dann – der Buchstabe, der der zweiten Spalte entspricht usw.). Schreiben Sie die Buchstaben in die Antworten Sie in einer Reihe, ohne Trennzeichen. Es ist nicht nötig, sie zwischen Buchstaben zu setzen.

R Lösung:

Schreiben wir den gegebenen Ausdruck in einfacherer Notation:

(x*y*¬z) + (x*y*z) + (x*¬y*¬z)=1

Dieser Ausdruck ist wahr, wenn mindestens eines von (x*y*¬z), (x*y*z), (x*¬y*¬z) gleich 1 ist. Konjunktion (logische Multiplikation) ist genau dann wahr, wenn Alle Aussagen sind wahr.

Zumindest eine dieser Disjunktionen x*y*¬z; x*y*z; x*¬y*¬z wird nur wahr sein, wenn x=1.

Also die Variable X entspricht der Spalte mit Variable 2 (Spalte 2).

Lassen y- Variable 1, z- Präm.3. Dann im ersten Fall x*¬y*¬z wird im zweiten Fall wahr sein x*y*¬z, und im dritten x*y*z.

Antwort: yxz

Das Symbol F bezeichnet einen der folgenden logischen Ausdrücke aus drei Argumenten: X, Y, Z. Angegeben ist ein Fragment der Wahrheitstabelle des Ausdrucks F (siehe Tabelle rechts). Welcher Ausdruck passt zu F?

X	Y	Z	F
0	0	0	0
1	0	1	1
0	1	0	1

1) X ∧ Y ∧ Z 2) ¬X ∨ Y ∨¬Z 3) X ∧ Y ∨ Z 4) X ∨ Y ∧ ¬Z

Lösung:

1) X ∧ Y ∧ Z = 1,0,1 = 0 (passt nicht in der 2. Zeile)

2) ¬X ∨ Y ∨¬Z = ¬0 ∨ 0 ∨ ¬0 = 1+0+1 = 1 (passt nicht in der 1. Zeile)

3) X ∧ Y ∨ Z = 0,1+0 = 0 (passt nicht in der 3. Zeile)

4) X ∨ Y ∧ ¬Z (entspricht F)

X ∨ Y ∧ ¬Z = 0 ∨ 0 ∧ ¬0 = 0+0,1 = 0

X ∨ Y ∧ ¬Z = 1 ∨ 0 ∧ ¬1 = 1+0,0 = 1

X ∨ Y ∧ ¬Z = 0 ∨ 1 ∧ ¬0 = 0+1,1 = 1

Antwort: 4

Gegeben sei ein Fragment der Wahrheitstabelle des Ausdrucks F. Welcher Ausdruck entspricht F?

A	B	C	F
0	1	1	1
1	0	0	0
1	0	1	1

1) (A → ¬B) ∨ C 2) (¬A ∨ B) ∧ C 3) (A ∧ B) → C 4) (A ∨ B) → C

Lösung:

1) (A → ¬B) ∨ C = (1 → ¬0) ∨ 0 = (1 → 1) + 0 = 1 + 0 = 1 (passt nicht in der 2. Zeile)

2) (¬A ∨ B) ∧ C = (¬1 ∨ 0) ∧ 1 = (0+0).1 = 0 (passt nicht in der 3. Zeile)

3) (A ∧ B) → C = (1 ∧ 0) → 0 = 0 → 0 = 1 (passt nicht in der 2. Zeile)

4) (A ∨ B) → C (entspricht F)

(A ∨ B) → C = (0 ∨ 1) → 1 = 1

(A ∨ B) → C = (1 ∨ 0) → 0 = 0

(A ∨ B) → C = (1 ∨ 0) → 1 = 1

Antwort: 4

Es wird ein logischer Ausdruck angegeben, der von 6 logischen Variablen abhängt:

X1 ∨ ¬X2 ∨ X3 ∨ ¬X4 ∨ X5 ∨ X6

Wie viele verschiedene Sätze von Variablenwerten gibt es, für die der Ausdruck wahr ist?

1) 1 2) 2 3) 63 4) 64

Lösung:

Falscher Ausdruck nur in 1 Fall: X1=0, X2=1, X3=0, X4=1, X5=0, X6=0

X1 ∨ ¬X2 ∨ X3 ∨ ¬X4 ∨ X5 ∨ X6 = 0 ∨ ¬1 ∨ 0 ∨ ¬1 ∨ 0 ∨ 0 = 0

Insgesamt gibt es 2 6 =64 Optionen, was wahr bedeutet

Antwort: 63

Es wird ein Fragment der Wahrheitstabelle des Ausdrucks F angegeben.

x1	x2	x3	x4	x5	x6	x7	F
0	1	0	1	1	1	0	0
1	1	0	1	0	1	0	1
0	1	0	1	1	0	1	0

Welcher Ausdruck passt zu F?

1) x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ x6 ∨ ¬x7
2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ x7
3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7
4) x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ x6 ∧ ¬x7

Lösung:

1) x1 ∨ x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 ∨ x6 ∨ ¬x7 = 0 + 1 + … = 1 (passt nicht in der 1. Zeile)

2) x1 ∨ ¬x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ x6 ∨ x7 = 0 + 0 + 0 + 0 + 0 + 1 + 0 = 1 (passt nicht in der 1. Zeile)

3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ ¬x6 ∧ x7 = 1,0. ...= 0 (entspricht nicht der 2. Zeile)

4) x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ x6 ∧ ¬x7 (entspricht F)

x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ x6 ∧ ¬x7 = 1.1.1.1.1.1.1 = 1

x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ ¬x5 ∧ x6 ∧ ¬x7 = 0. … = 0

Antwort: 4

x1	x2	x3	x4	x5	x6	x7	x8	F
		0				1		1
1		0			1			0
			1				0	1

Welcher Ausdruck kann F sein?

1) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7 ∧ ¬x8
2) ¬x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7 ∨ x8
3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ ¬x6 ∧ ¬x7 ∧ ¬x8
4) ¬x1 ∨ ¬x2 ∨ ¬x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7 ∨ ¬x8

Lösung:

1) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 ∧ x6 ∧ ¬x7 ∧ ¬x8 = x1 . ¬x2. 0 . ... = 0 (passt nicht in der 1. Zeile)

2) ¬x1 ∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7 ∨ x8 (entspricht F)

3) ¬x1 ∧ x2 ∧ ¬x3 ∧ x4 ∧ x5 ∧ ¬x6 ∧ ¬x7 ∧ ¬x8 = … ¬x7 ∧ ¬x8 = … ¬1 ∧ ¬x8 = … 0 ∧ ¬x8 = 0 (passt nicht auf 1 - te Zeile)

4) ¬x1 ∨ ¬x2 ∨ ¬x3 ∨ ¬x4 ∨ ¬x5 ∨ ¬x6 ∨ ¬x7 ∨ ¬x8 = ¬x1 ∨ ¬x2 ∨ ¬x3 … = ¬1 ∨ ¬x2 ∨ ¬0 .. = 1 (nicht Übereinstimmungen in der 2. Zeile)

Antwort: 2

Gegeben ist ein Fragment der Wahrheitstabelle für den Ausdruck F:

x1	x2	x3	x4	x5	x6	x7	F
0	0	1	1	0	0	1	0
0	1	0	0	1	1	0	1
0	0	0	0	1	1	1	1
1	0	1	0	1	1	0	1
0	1	1	1	0	1	0	1

Finden Sie in der vollständigen Wahrheitstabelle dieses Ausdrucks die minimal mögliche Anzahl verschiedener Zeilen, in denen der Wert x5 mit F übereinstimmt.

Lösung:

Minimal mögliche Anzahl unterschiedlicher Zeilen, in denen x5 mit F = 4 übereinstimmt

Antwort: 4

Gegeben ist ein Fragment der Wahrheitstabelle für den Ausdruck F:

x1	x2	x3	x4	x5	x6	x7	x8	F
0	0	1	1	0	0	1	0	0
0	1	0	0	1	1	0	1	1
0	0	0	0	1	1	1	1	1
1	0	1	0	1	1	0	1	1
0	1	1	1	0	1	0	0	1

Finden Sie die maximal mögliche Anzahl unterschiedlicher Zeilen in der vollständigen Wahrheitstabelle dieses Ausdrucks, in denen der Wert x6 nicht mit F übereinstimmt.

Lösung:

Maximal mögliche Anzahl = 2 8 = 256

Die maximal mögliche Anzahl verschiedener Zeilen, in denen der Wert x6 nicht mit F = 256 – 5 = 251 übereinstimmt

Antwort: 251

Gegeben ist ein Fragment der Wahrheitstabelle für den Ausdruck F:

x1	x2	x3	x4	x5	x6	x7	F
0	0	1	1	0	0	1	0
0	1	0	0	1	1	0	1
0	0	0	0	1	1	1	1
1	0	1	0	1	1	0	1
0	1	1	1	0	1	0	1

Finden Sie die maximal mögliche Anzahl verschiedener Zeilen der vollständigen Wahrheitstabelle dieses Ausdrucks, in denen der Wert ¬x5 ∨ x1 mit F übereinstimmt.

Lösung:

1+0=1 – passt nicht zu F

0+0=0 – passt nicht zu F

0+0=0 – passt nicht zu F

0+1=1 – stimmt mit F überein

1+0=1 – stimmt mit F überein

2 7 = 128 – 3 = 125

Antwort: 125

Jeder boolesche Ausdruck A und B hängt von demselben Satz von 6 Variablen ab. In den Wahrheitstabellen hat jeder dieser Ausdrücke genau 4 Einheiten in der Wertespalte. Was ist die minimal mögliche Anzahl von Einsen in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∨ B?

Lösung:

Antwort: 4

Jeder boolesche Ausdruck A und B hängt von demselben Satz von 7 Variablen ab. In den Wahrheitstabellen hat jeder dieser Ausdrücke genau 4 Einheiten in der Wertespalte. Was ist die maximal mögliche Anzahl von Einsen in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∨ B?

Lösung:

Antwort: 8

Jeder boolesche Ausdruck A und B hängt von demselben Satz von 8 Variablen ab. In den Wahrheitstabellen hat jeder dieser Ausdrücke genau 5 Einheiten in der Wertespalte. Was ist die minimal mögliche Anzahl von Nullen in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∧ B?

Lösung:

2 8 = 256 – 5 = 251

Antwort: 251

Jeder boolesche Ausdruck A und B hängt von demselben Satz von 8 Variablen ab. In den Wahrheitstabellen hat jeder dieser Ausdrücke genau 6 Einheiten in der Wertespalte. Was ist die maximal mögliche Anzahl von Nullen in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∧ B?

Lösung:

Antwort: 256

Die booleschen Ausdrücke A und B hängen jeweils von demselben Satz von 5 Variablen ab. In den Wahrheitstabellen beider Ausdrücke gibt es keine übereinstimmenden Zeilen. Wie viele Einsen werden in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∧ B enthalten sein?

Lösung:

In den Wahrheitstabellen beider Ausdrücke gibt es keine übereinstimmenden Zeilen.

Antwort: 0

Die booleschen Ausdrücke A und B hängen jeweils von demselben Satz von 6 Variablen ab. In den Wahrheitstabellen beider Ausdrücke gibt es keine übereinstimmenden Zeilen. Wie viele Einsen werden in der Wertespalte der Wahrheitstabelle des Ausdrucks A ∨ B enthalten sein?

Lösung:

Antwort: 64

Jeder der booleschen Ausdrücke A und B hängt von demselben Satz von 7 Variablen ab. In den Wahrheitstabellen beider Ausdrücke gibt es keine übereinstimmenden Zeilen. Was ist die maximal mögliche Anzahl von Nullen in der Wertespalte der Wahrheitstabelle des Ausdrucks ¬A ∨ B?

Lösung:

A=1,B=0 => ¬0 ∨ 0 = 0 + 0 = 0

Antwort: 128

Jeder der booleschen Ausdrücke F und G enthält 7 Variablen. Es gibt genau 8 identische Zeilen in den Wahrheitstabellen der Ausdrücke F und G, und genau 5 davon haben eine 1 in der Wertespalte. Wie viele Zeilen der Wahrheitstabelle für den Ausdruck F ∨ G enthalten eine 1 in der Wertespalte? ?

Lösung:

Es gibt genau 8 identische Zeilen und genau 5 davon haben eine 1 in der Wertespalte.

Das bedeutet, dass genau 3 davon eine 0 in der Wertespalte haben.

Antwort: 125

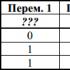
Die logische Funktion F ist durch den Ausdruck (a ∧ ¬c) ∨ (¬b ∧ ¬c) gegeben. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen a, b, c entspricht.

?	?	?	F
0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	0

Schreiben Sie in Ihrer Antwort die Buchstaben a, b, c in der Reihenfolge, in der ihre entsprechenden Spalten erscheinen.

Lösung:

(a . ¬c) + (¬b . ¬c)

Wenn c 1 ist, ist F Null, sodass die letzte Spalte c ist.

Um die erste und zweite Spalte zu bestimmen, können wir die Werte aus der 3. Zeile verwenden.

(a . 1) + (¬b . 1) = 0

Antwort: ABC

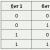
Die logische Funktion F ist durch den Ausdruck (a ∧ c)∨ (¬a ∧ (b ∨ ¬c)) gegeben. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen a, b, c entspricht.

Basierend auf der Tatsache, dass, wenn a=0 und c=0, dann F=0 ist, und den Daten aus der zweiten Zeile können wir schließen, dass die dritte Spalte enthält B.

Antwort: Taxi

Die logische Funktion F ist gegeben durch x ∧ (¬y ∧ z ∧ ¬w ∨ y ∧ ¬z). Die Abbildung zeigt ein Fragment der Wahrheitstabelle der Funktion F, das alle Argumentmengen enthält, für die die Funktion F wahr ist. Bestimmen Sie, welche Spalte der Wahrheitstabelle der Funktion F jeder der Variablen x, y, z, w entspricht.

?	?	?	?	F
0	1	0	1	1
0	1	1	0	1
1	1	0	1	1

Schreiben Sie in Ihrer Antwort die Buchstaben x, y, z, w in der Reihenfolge, in der ihre entsprechenden Spalten erscheinen.

Lösung:

x ∧ (¬y ∧ z ∧ ¬w ∨ y ∧ ¬z)

X. (¬y . z . ¬w . y . ¬z)

Basierend auf der Tatsache, dass bei x=0 dann F=0 ist, können wir schließen, dass die zweite Spalte enthält X.

Antwort: wxzy

Analyse der Aufgabe 2 des Einheitlichen Staatsexamens 2017 in Informatik aus dem Demoversionsprojekt. Dies ist eine Aufgabe mit einem einfachen Schwierigkeitsgrad. Die ungefähre Bearbeitungszeit für die Aufgabe beträgt 3 Minuten.

Getestete Inhaltselemente: Fähigkeit, Wahrheitstabellen und logische Schaltkreise zu erstellen. Im Einheitlichen Staatsexamen geprüfte Inhaltselemente: Aussagen, logische Operationen, Quantoren, Wahrheit von Aussagen.

Aufgabe 2:

Logikfunktion F ist durch den Ausdruck gegeben X /\¬ j /\ (¬ z \/ w).
Die Abbildung zeigt einen Ausschnitt der Wahrheitstabelle der Funktion F enthaltend Alle F WAHR.
Bestimmen Sie die Spalte der Wahrheitstabelle der Funktion F Jede der Variablen entspricht w, X, j, z.

Schreiben Sie die Buchstaben in Ihre Antwort w, x, y, z in der Reihenfolge, in der die entsprechenden Spalten erscheinen (zuerst – der Buchstabe, der der ersten Spalte entspricht; dann – der Buchstabe, der der zweiten Spalte entspricht usw.) Schreiben Sie die Buchstaben in der Antwort hintereinander, es ist nicht nötig, welche einzufügen Trennzeichen zwischen den Buchstaben.

Beispiel. Wenn die Funktion durch den Ausdruck ¬ gegeben wäre X \/ j, abhängig von zwei Variablen: X Und j, und ein Fragment seiner Wahrheitstabelle wurde gegeben, enthaltend Alle Mengen von Argumenten, für die die Funktion gilt F WAHR.

Dann würde die erste Spalte der Variablen entsprechen j und die zweite Spalte ist eine Variable X. Die Antwort hätte lauten sollen: yx.

Antwort: ________

X /\¬ j /\ (¬ z \/ w)

Eine Konjunktion (logische Multiplikation) ist genau dann wahr, wenn alle Aussagen wahr sind. Daher die Variable X 1 .

Also die Variable X entspricht der Spalte mit Variable 3.

Variable ¬y Die Spalte mit dem Wert muss übereinstimmen 0 .

Eine Disjunktion (logische Addition) zweier Aussagen ist genau dann wahr, wenn mindestens eine Aussage wahr ist.
Disjunktion ¬z\/w in dieser Zeile ist nur dann wahr, wenn z=0, w=1.

Also die Variable ¬z entspricht Spalte mit Variable 1 (1 Spalte), Variable w entspricht der Spalte mit Variable 4 (Spalte 4).