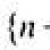Parallel- und Reihenschaltung von Widerständen, Kondensatoren und Induktivitäten. Verbindung der Komponenten: Kondensator und Spule in Reihe geschaltet

Gehen Sie wie zuvor davon aus, dass der Strom im Stromkreis gesetzeskonform schwankt

und berechnen Sie die Spannung zwischen den Enden des Stromkreises u. Denn wenn die Leiter in Reihe geschaltet werden, addieren sich die Spannungen, die gewünschte Spannung u ist die Summe von drei Spannungen: Widerstand, Kapazität und Induktivität, und jede dieser Spannungen ändert sich, wie wir gesehen haben, im Laufe der Zeit gemäß dem Kosinusgesetz:

, (5)

, (6)

Um diese drei Schwingungen zu addieren, verwenden wir ein Vektorspannungsdiagramm. Spannungsschwankungen am Widerstand werden darauf durch einen Vektor dargestellt, der entlang der Stromachse verläuft und die Länge hat, während Spannungsschwankungen an der Kapazität und Induktivität durch Vektoren dargestellt werden, die senkrecht zur Stromachse liegen und die Längen haben ( ICH m/w C) Und ( ICH m w L) (Abb. 9.). Stellen wir uns vor, dass diese Vektoren mit der Winkelgeschwindigkeit w gegen den Uhrzeigersinn um einen gemeinsamen Ursprung rotieren. Anschließend werden die Projektionen der Vektoren , und , auf die aktuelle Achse jeweils durch die Formeln (5)-(7) beschrieben. Offensichtlich die Projektion des Gesamtvektors auf die aktuelle Achse

gleich der Summe, also gleich der Gesamtspannung am Schaltungsabschnitt. Der Maximalwert dieser Spannung entspricht dem Vektormodul. Dieser Wert lässt sich leicht geometrisch ermitteln. Zunächst empfiehlt es sich, den Modul des Vektors zu ermitteln:

,

und dann nach dem Satz des Pythagoras:

. (8)

Das geht auch aus der Abbildung hervor

. (9)

Für die Spannung an einem Abschnitt des Stromkreises können wir schreiben

wobei die Spannungsamplitude und die Phasenverschiebung zwischen Strom und Spannung durch die Formeln (8), (9) bestimmt werden. Wenn , dann eilt die Spannung dem Strom in Phase voraus, andernfalls eilt die Spannung der Phase nach.

Formel (8) ähnelt dem Ohmschen Gesetz in dem Sinne, dass die Spannungsamplitude proportional zur Stromamplitude ist. Daher wird es manchmal als Ohmsches Gesetz für Wechselstrom bezeichnet. Es muss jedoch beachtet werden, dass diese Formel nur für Amplituden gilt, nicht jedoch für Momentanwerte und . Größe

Als Stromkreiswiderstand bezeichnet man bei Wechselstrom den Wert

wird als Reaktanz des Stromkreises und als Wert bezeichnet R- aktiver Widerstand.

Die resultierenden Formeln gelten auch für einen geschlossenen Stromkreis, der einen Wechselspannungsgenerator enthält, sofern darunter R, C Und L ihre Bedeutung für die gesamte Kette verstehen (z. B R stellt den gesamten aktiven Widerstand des Stromkreises dar, einschließlich des Innenwiderstands des Generators). In diesem Fall sollten alle Formeln ersetzt werden u auf der EMK des Generators. Tatsächlich war es trotz all unserer Überlegungen gleichgültig, wo genau die Kapazität, die Induktivität und der Widerstand konzentriert sind. Daher können wir in einem geschlossenen Stromkreis (Abb. 8) den gesamten aktiven Widerstand des Stromkreises berücksichtigen, einschließlich des Innenwiderstands des Stromkreises Generator und - Kapazität und Induktivität des Stromkreises und ersetzen Sie den realen Generator durch einen imaginären, dessen Innenwiderstand Null ist. In diesem Fall die Spannung u zwischen Punkten A Und B wird gleich der EMK des Generators sein. Daraus folgt, dass die Formeln (8), (9) auch für einen geschlossenen Wechselstromkreis gelten, wenn wir durch , , ihre Bedeutung für den gesamten Stromkreis verstehen und sie in allen Formeln ersetzen u auf der EMK des Generators.

Nach den Gleichungen der Elemente

. (15.1)

Wir haben einen aktuellen Komplex gefunden. Nebenbei erhielten wir im Nenner den komplexen Widerstand des Zwei-Terminal-Netzwerks , aktiver Widerstand eines Netzwerks mit zwei Anschlüssen und Reaktanz eines Netzwerks mit zwei Anschlüssen .

Phasenresonanz Ein Netzwerk mit zwei Anschlüssen ist ein Modus, in dem Strom und Spannung des Netzwerks mit zwei Anschlüssen in Phase sind: . In diesem Fall sind Reaktanz und Blindleitfähigkeit des Zweipols gleich Null.

Spannungsresonanz Als Zweipolschaltung bezeichnet man einen Modus, in dem die Spannungen der Schaltungselemente maximal kompensiert werden. Die Impedanz des Zweipolnetzes ist minimal.

Resonanz von Strömen Als Zweipolschaltung bezeichnet man einen Modus, in dem die Ströme der Schaltungselemente maximal kompensiert werden. Der Gesamtwiderstand des Zweipolnetzes ist maximal.

Bei einer Reihenschaltung aus Widerstand, Induktivität und Kondensator fällt die Phasenresonanz mit der Spannungsresonanz zusammen. Die Resonanzfrequenz wird durch die Formel bestimmt

was aus der Gleichheit der Nullreaktanz abgeleitet wird: .

Abhängigkeit der effektiven Spannungswerte von der Frequenz für eine Reihenschaltung R, L, C in Abb. dargestellt. 15.3. Ausdrücke zur Berechnung dieser Spannungen erhält man durch Multiplikation des effektiven Stromwerts (Formel 15.2) mit den Impedanzen der Elemente: , , (siehe Abschnitt 12).

Erstellen wir ein Vektordiagramm von Strom und Spannung (Abb. 15.4, der Fall ist hier dargestellt). U L > U C). Dies geht am einfachsten, wenn die Anfangsphase des Stroms Null ist: . Dann wird der Vektor, der den aktuellen Komplex darstellt, in einem Winkel zur realen Achse der komplexen Ebene ausgerichtet. Die Spannung am Widerstand ist in Phase mit dem Strom, sodass der Vektor, der den Spannungskomplex am Widerstand darstellt, in die gleiche Richtung gerichtet ist wie der Vektor, der den Stromkomplex darstellt.

Reis. 15.3.

Reis. 15.4.

Reis. 15.5.

Die Spannung an der Induktivität ist dem Strom in der Phase um einen Winkel voraus, sodass der Vektor, der den Spannungskomplex an der Induktivität darstellt, in einem Winkel zum Vektor gerichtet ist, der den Stromkomplex darstellt. Die Spannung am Kondensator eilt dem Strom um einen Winkel in der Phase nach, sodass der Vektor, der den Spannungskomplex am Kondensator darstellt, in einem Winkel zum Vektor gerichtet ist, der den Stromkomplex darstellt. Der Vektor, der den Komplex der angelegten Spannung darstellt, ist gleich der Summe der Vektoren, die die komplexen Spannungen an Widerstand, Kondensator und Spule darstellen. Die Längen aller Vektoren sind proportional zu den Effektivwerten der entsprechenden Größen. Das heißt, um Vektoren zu zeichnen, müssen Sie den Maßstab festlegen, zum Beispiel: 1 Zentimeter entspricht 20 Volt, 1 Zentimeter entspricht 5 Ampere.

Das Vektordiagramm für den Resonanzmodus ist in Abb. dargestellt. 15.5.

Berechnen wir das Verhältnis der effektiven Spannungswerte an der Induktivität und am Kondensator zum effektiven Wert der Quellenspannung im Resonanzmodus.

Berücksichtigen wir, dass sich bei Resonanz die Spannungen an der Spule und am Kondensator vollständig gegenseitig kompensieren (Spannungsresonanz) und daher die Quellenspannung gleich der Spannung am Widerstand ist: (Abb. 15.5). Wir verwenden den Zusammenhang zwischen den Effektivwerten von Strom und Spannung für Widerstand, Spule und Kondensator sowie die Formel für die Resonanzfrequenz. Wir bekommen:

Wo .

Die Menge wird aufgerufen Wellenimpedanz Schwingkreis und wird mit dem Buchstaben r bezeichnet. Die Beziehung wird mit dem Buchstaben Q bezeichnet und heißt Qualitätsfaktor Schwingkreis. Es bestimmt die Verstärkungseigenschaften der Schaltung bei der Resonanzfrequenz. In guten Schaltkreisen kann der Gütefaktor in der Größenordnung von mehreren Hundert liegen, das heißt, im Resonanzmodus kann die Spannung an Spule und Kondensator hunderte Male größer sein als die am Zweipolnetzwerk anliegende Spannung.

Resonanz wird in der Elektrotechnik und Elektronik häufig zur Verstärkung sinusförmiger Spannungen und Ströme sowie zur Trennung von Schwingungen bestimmter Frequenzen von komplexen Schwingungen eingesetzt. Allerdings führen unerwünschte Resonanzen in Informationsstromkreisen zur Entstehung und Verstärkung von Störungen und in Stromkreisen zu gefährlich hohen Spannungen und Strömen.

Wenn in einem Entwurfsdiagramm eine Spule und ein Kondensator in Reihe geschaltet sind, kann jedes dieser Elemente des Stromkreises durch aktive und reaktive Widerstände oder aktive und reaktive Leitfähigkeiten dargestellt werden.

Für Berechnungen ist Abb. ein einfacheres Diagramm. 14.1, a, wo die Elemente in Reihe geschaltet sind, und im Diagramm in Abb. 14.1, b sind sie gemischt verbunden.

Nehmen wir an, dass die Parameter der Spule R1, L und des Kondensators R2, C bekannt sind; Stromkreis i = I m sinωt.

Es ist notwendig, die Spannung in den Abschnitten des Stromkreises und die Leistung zu bestimmen.

Vektordiagramm und Zielimpedanz

Der Momentanwert der Gesamtspannung kann durch die Summe der Momentanspannungen an den einzelnen Elementen der Schaltung dargestellt werden:

u = u 1R + u L + u C + u 2R ,

Ich meine Phasenfehlanpassung Wirk- und Blindspannung, die Gesamtspannung ergibt sich durch Vektoraddition:

U = U 2R + U L + U C + U 2R

Um ein Vektordiagramm zu erstellen, finden wir:

U 1R = IR 1; U 2R = IR 2 ; U L = IX L ; U C = IX C .

Abhängig vom Verhältnis der Induktivitäts- und Kapazitätsreaktanzwerte können drei Fälle festgestellt werden:

1. X L >X C . Für diesen Fall ist das Vektordiagramm in Abb. dargestellt. 14.2. Das Diagramm zeigt Spannungsdreiecke für Spule und Kondensator und findet die Spannungsvektoren U 1 und U 2 an diesen Elementen.

Vektorsumme der Spannungen U 1 + U 2 = U Gibt die Gesamtspannung im Stromkreis an. Gleichzeitig ist der Vektor U die Hypotenuse eines rechtwinkligen Spannungsdreiecks, dessen Schenkel die Wirk- und Blindspannungen des Stromkreises sind ( U a Und U r ). Da die Vektoren der Wirkspannungskomponenten in eine Richtung gerichtet sind, addieren sich ihre Zahlenwerte: U a = U 1R + U 2R.

Die Vektoren der Blindspannungskomponenten sind entlang einer Geraden in entgegengesetzte Richtungen gerichtet und erhalten daher unterschiedliche Vorzeichen: Die reaktive Induktivitätsspannung gilt als positiv und die Kapazitätsspannung als negativ: U p = U L - U C.

Mit dem gleichen Strom in allen Elementen des Stromkreises U L > U C . Aktuell der Gesamtspannung hinterherhinkt in Phase pro Winkel φ . Aus dem Spannungsdreieck folgt

Wo R = R 1 + R 2 Und X = XL - X C Gesamt-, Wirk- und Reaktanzwiderstand des Stromkreises. Der Gesamtwiderstand des Stromkreises beträgt Z.

Diese Widerstände lassen sich grafisch durch die Seiten eines rechtwinkligen Widerstandsdreiecks darstellen, das man auf bekannte Weise aus einem Spannungsdreieck erhält.

Schaltungsimpedanz Z ist der Proportionalitätskoeffizient zwischen den Effektivwerten des Stroms und der Gesamtspannung des Stromkreises:

U = IZ; I = U/Z; Z = U/I.

Aus den Spannungs- und Widerstandsdreiecken werden folgende Größen ermittelt:

Der Phasenverschiebungswinkel zwischen Spannung und Strom im Stromkreis ist positiv ( φ >0) (Phasenströme werden vom Stromvektor aus gezählt).

2. XL< Х C Das Vektordiagramm ist in Abb. dargestellt. 14.3, wo U L φ <0.

Re Der aktive Widerstand des Stromkreises ist kapazitiver Natur .

Die Berechnungsformeln für den ersten Fall bleiben für den zweiten Fall unverändert.

3. X L = X C . In diesem Fall sind die Blindspannungsanteile von Spule und Kondensator gleich groß und kompensieren sich gegenseitig: U L = U C (Abb. 14.4). Daher sind der Blindanteil der Gesamtspannung und die Gesamtreaktanz gleich Null und der Gesamtwiderstand des Stromkreises Z = R.

Die Gesamtspannung ist phasengleich mit dem Strom und entspricht betragsmäßig der Wirkspannung

Spannungskomponente.

Der Phasenwinkel φ zwischen Strom und Gesamtspannung ist Null.

Der Strom im Stromkreis und die Gesamtspannung hängen durch die Formel zusammen

U = IR oder I = U/R.

Im Fall X L = X C tritt im Stromkreis das Phänomen der Spannungsresonanz auf.

Energieprozess in einem Stromkreis mit einer Reihenschaltung aus einem Kondensator und einer Spule

Aus dem Spannungsdreieck lässt sich leicht ein Leistungsdreieck ermitteln, aus dem sich die bereits bekannten Formeln ergeben:

Auch Blindleistungen gehen mit unterschiedlichen Vorzeichen in die Berechnungen ein: Die induktive Leistung ist positiv und die kapazitive Leistung ist negativ.

Dementsprechend kann das Vorzeichen der Blindleistung des gesamten Stromkreises das eine oder das andere sein, wie aus den Formeln (14.2) folgt.
Bei φ>0 Q>0 ; bei φ<0 Q<0.

Wirkleistung ist in jedem Winkel positiv, da cos φ =cos(- φ ).

Auch die Scheinleistung ist immer positiv. Basierend auf den Formeln (14.2) können wir schließen, dass in der betrachteten Schaltung eine Umwandlung elektrischer Energie (P ≠ 0) und ein Austauschprozess zwischen Generator und Empfänger (Q ≠ 0) stattfindet φ ≠ 0).

Energieprozesse sind in diesem Fall komplexer als in den zuvor diskutierten einfachen Schaltkreisen. Die Komplikation erklärt sich aus der Tatsache, dass neben dem Energieaustausch zwischen Generator und Empfänger auch ein Energieaustausch innerhalb des Empfängers zwischen der Spule und dem Kondensator stattfindet.

Merkmale des Energieprozesses in einem Stromkreis mit einer Reihenschaltung aus Spule und Kondensatoren sind in Abb. dargestellt. 14.5, das Diagramme der Momentanleistung einzelner Elemente und der Schaltung als Ganzes zeigt X L = X C.

Spule und Kondensator sammeln während eines Halbzyklus gleiche Energiemengen. Im ersten Viertel der Periode jedoch, wenn der Strom ansteigt und die Spannung am Kondensator abnimmt, sammelt sich Energie im Magnetfeld der Spule an und nimmt im elektrischen Feld des Kondensators ab, und die Änderungsrate der Energie (Leistung) nimmt ab ) ist zu jeder Zeit gleich. Dies lässt vermuten, dass der Energieaustausch nur im Empfänger zwischen den Spulen stattfindet
und ein Kondensator.

Um elektrische Energie in eine andere Form umzuwandeln, erhält der Empfänger diese von einem Generator mit einer Durchschnittsgeschwindigkeit (Leistung) R.

Probleme zum Thema und ein Beispiel zur Lösung eines Problems für eine Schaltung mit einer Reihenschaltung aus einem Kondensator und einer Spule