妥当な時間内に3つの方法でN番目のフィボナッチ数を見つける：動的計画法の基本。合理的な時間で3つの方法でN番目のフィボナッチ数を見つける：動的計画法の基本

フィボナッチ数のプログラマーはすでにうんざりしているはずです。それらの計算の例はどこでも使用されます。これらの数字が提供するものからすべて最も単純な例再帰。そしてまた彼らは良い手本動的計画法。しかし、実際のプロジェクトでは、このように計算する必要がありますか？必要なし。再帰も動的計画法も理想的なオプションではありません。また、浮動小数点数を使用した閉じた式ではありません。今、私はあなたに正しい方法を教えます。しかし、最初に、すべての既知の解決策を見てみましょう。

コードはPython3用ですが、Python2でも機能するはずです。

まず、定義を思い出させてください。

F n \ u003d F n-1 + F n-2

そして、F 1 \ u003d F 2 \ u003d1。

閉じた式

詳細は省略しますが、希望する人は式の導出に慣れることができます。アイデアは、F n = x nであるxがあると仮定し、xを見つけることです。

何をしますか

xn-2を減らします

二次方程式を解きます。

「黄金分割」ϕ =（1 +√5）/ 2が成長するところから。元の値を代入してさらに計算を行うと、次のようになります。

これは、Fnの計算に使用するものです。

__future__からインポート除算importmath def fib（n）：SQRT5 = math.sqrt（5）PHI =（SQRT5 + 1）/ 2 return int（PHI ** n / SQRT5 + 0.5）

良い：
小さいnのための速くて簡単
悪い：
浮動小数点演算が必要です。 nが大きいほど、より高い精度が必要になります。
悪の：
複素数を使用してFnを計算することは、数学的な観点からは美しいですが、コンピューターの観点からは醜いです。

再帰

すでに何度も見てきた最も明白な解決策-おそらく再帰とは何かの例として。完全を期すためにもう一度繰り返します。 Pythonでは、次の1行で記述できます。

fib =ラムダn：n> 2の場合はfib（n-1）+ fib（n-2）、それ以外の場合は1

良い：
数学的定義を繰り返す非常に単純な実装
悪い：
指数関数的なランタイム。大きいnの場合は非常にゆっくり
悪の：
スタックオーバーフロー

暗記

再帰的ソリューションには大きな問題があります。計算の重複です。 fib（n）が呼び出されると、fib（n-1）とfib（n-2）がカウントされます。ただし、fib（n-1）がカウントされると、独立してfib（n-2）が再度カウントされます。つまり、fib（n-2）は2回カウントされます。推論を続けると、fib（n-3）が3回カウントされることがわかります。交差点が多すぎます。

したがって、結果を再度カウントしないように、結果を覚えておく必要があります。このソリューションは、時間とメモリを直線的に消費します。ソリューションで辞書を使用していますが、単純な配列を使用することもできます。

M =（0：0、1：1）def fib（n）：if n in M：return M [n] M [n] = fib（n-1）+ fib（n-2）return M [n]

（Pythonでは、これはデコレータfunctools.lru_cacheを使用して実行することもできます。）

良い：
再帰を覚えている解決策に変えるだけです。指数関数的な実行時間を線形実行時間に変換します。これにより、より多くのメモリが消費されます。
悪い：
多くのメモリを浪費します
悪の：
再帰のようなスタックオーバーフローの可能性

動的計画法

暗記して解くと、前の結果がすべて必要なわけではなく、最後の2つだけが必要であることが明らかになります。また、fib（n）から開始して逆方向に進む代わりに、fib（0）から開始して前に進むことができます。次のコードは、実行時間が線形で、メモリ使用量が固定されています。実際には、再帰的な関数呼び出しや関連する作業がないため、ソリューションの速度はさらに速くなります。そして、コードはより単純に見えます。

このソリューションは、動的計画法の例としてよく引用されます。

Def fib（n）：a = 0 b = 1 for __ in range（n）：a、b = b、a + b return a

良い：
小さいnの単純なコードに対して高速
悪い：
まだ線形ランタイム
悪の：
はい、特別なことは何もありません。

行列代数

そして最後に、最も照らされていないが、ほとんど正しい解決策、時間とメモリの両方をインテリジェントに使用します。また、任意の均一な線形シーケンスに拡張することもできます。アイデアは行列を使用することです。それを見るだけで十分です

そしてこれの一般化はそれです

以前に取得したxの2つの値（そのうちの1つは黄金比）は、行列の固有値です。したがって、閉じた式を導出する別の方法は、行列方程式と線形代数を使用することです。

では、なぜこのフレーズが役立つのでしょうか。べき乗が対数時間で実行できるという事実。これは二乗によって行われます。肝心なのは

最初の式が偶数Aに使用され、2番目の式が奇数に使用される場合。行列の乗算を整理するだけで、すべての準備が整います。次のコードが見つかります。理解しやすいので、powの再帰的な実装を編成しました。ここで反復バージョンを参照してください。

Def pow（x、n、I、mult）： "" "xをnの累乗で返します。Iがmultで乗算される単位行列であり、nが正の整数であると仮定します" "" n == 0の場合：return I elif n == 1：return x else：y = pow（x、n // 2、I、mult）y = mult（y、y）if n％2：y = mult（x、y）return y def Identity_matrix （n）： "" "n行n列の単位行列を返します" "" r = list（range（n））return [for j in r] def matrix_multiply（A、B）：BT = list（zip（* B））return [for row_a in A] def fib（n）：F = pow（[、]、n、identity_matrix（2）、matrix_multiply）return F

良い：
固定メモリサイズ、対数時間
悪い：
コードはもっと複雑です
悪の：
それほど悪くはありませんが、行列を操作する必要があります

パフォーマンスの比較

動的計画法の変形と行列のみを比較する価値があります。それらを数nの桁数で比較すると、行列の解は線形であり、動的計画法を使用した解は指数関数的であることがわかります。実用的な例は、20万文字を超える数値であるfib（10 ** 6）の計算です。

N = 10 ** 6
fib_matrixを計算します。fib（n）の合計は208988桁で、計算には0.24993秒かかりました。
fib_dynamicを計算します。fib（n）の合計は208988桁で、計算には11.83377秒かかりました。

理論的見解

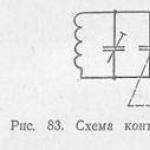
上記のコードとは直接関係ありませんが、この発言はまだ興味深いものです。次のグラフについて考えてみます。

AからBまでの長さnのパスの数を数えましょう。たとえば、n = 1の場合は1つのパス1があります。n= 2の場合も1つのパス01があります。n= 3の場合は2つのパスがあります。、001および101AからBまでの長さnのパスの数が正確にFnであることを非常に簡単に示すことができます。グラフの隣接行列を作成すると、上記と同じ行列が得られます。隣接行列Aが与えられた場合、Aでの出現、nはグラフ内の長さnのパスの数であることがグラフ理論からよく知られている結果です（映画「グッドウィルハンティング」で言及されている問題の1つ）。

なぜ端にそのような指定があるのですか？グラフ上のパスの両方向のシーケンスの無限のシンボルの無限のシーケンスを考えると、記号力学のシステムの一種である「有限タイプのサブシフト」と呼ばれるものが得られることがわかります。具体的には、この有限型のサブシフトは「黄金比シフト」と呼ばれ、一連の「禁止された単語」によって与えられます（11）。言い換えると、両方向に無限のバイナリシーケンスが得られ、それらのペアは隣接しません。この力学系の位相的エントロピーは黄金比ϕに等しくなります。この数が数学のさまざまな分野で定期的にどのように現れるかは興味深いです。

フィボナッチ数-これは一連の数値であり、次の各数値は前の2つの数値の合計に等しくなります：1、1、2、3、5、8、13、...。時々、シリーズはゼロから始まります：0、1、1、2、3、5、...。のこの場合最初のオプションを使用します。

方式：

F1 = 1
F2 = 1
F n \ u003d F n-1 + F n-2

計算例：

F 3 \ u003d F 2 + F 1 \ u003d 1 + 1 \ u003d 2
F 4 \ u003d F 3 + F 2 \ u003d 2 + 1 \ u003d 3
F 5 \ u003d F 4 + F 3 \ u003d 3 + 2 \ u003d 5
F 6 \ u003d F 5 + F 4 \ u003d 5 + 3 \ u003d 8
...

whileループを使用してフィボナッチ数列のn番目の数を計算する

変数fib1とfib2に、シリーズの最初の2つの要素の値を割り当てます。つまり、変数に単位を割り当てます。
値を取得したい要素の番号をユーザーに尋ねます。変数nに番号を割り当てます。
最初の2つの要素がすでに考慮されているため、次の手順をn〜2回実行します。
1. fib1とfib2を追加し、結果をfib_sumなどの一時ストレージ変数に割り当てます。
2. fib1をfib2に設定します。
3. fib2をfib_sumに設定します。
fib2の値を表示します。

ノート。ユーザーが1または2を入力すると、ループの本体は実行されず、fib2の元の値が表示されます。

fib1 = 1 fib2 = 1 n = input（）n = int（n）i = 0 while i< n - 2 : fib_sum = fib1 + fib2 fib1 = fib2 fib2 = fib_sum i = i + 1 print (fib2)

コードのコンパクトバージョン：

fib1 = fib2 = 1 n = int（input（「フィボナッチ数列の要素番号：」））-2 while n> 0：fib1、fib2 = fib2、fib1 + fib2 n- = 1 print（fib2）

forループでフィボナッチ数を出力する

この場合、フィボナッチ数列の目的の要素の値だけでなく、それまでのすべての数値も表示されます。これを行うために、fib2値の出力はループに配置されます。

fib1 = fib2 = 1 n = int（input（））if n< 2 : quit() print (fib1, end= " " ) print (fib2, end= " " ) for i in range (2 , n) : fib1, fib2 = fib2, fib1 + fib2 print (fib2, end= " " ) print ()

実行例：

10 1 1 2 3 5 8 13 21 34 55

フィボナッチ数列のn番目の数の再帰的計算

n = 1またはn = 2の場合、フィボナッチ数列の1番目と2番目の要素は1に等しいため、呼び出し元のブランチに1を返します。
他のすべての場合は、引数n-1およびn-2を使用して同じ関数を呼び出します。2回の呼び出しの結果を加算して、プログラムの呼び出し側ブランチに返します。

def fibonacci（n）：if n in（1、2）：return 1 return fibonacci（n-1）+ fibonacci（n-2）print（fibonacci（10））

n = 4としましょう。そうすると、fibonacci（3）とfibonacci（2）が再帰的に呼び出されます。 2番目は1つを返し、最初はさらに2つの関数呼び出し（fibonacci（2）とfibonacci（1））になります。どちらの呼び出しも1つ、合計2つを返します。したがって、fibonacci（3）を呼び出すと、番号2が返されます。これは、fibonacci（2）を呼び出すと番号1に追加されます。結果3は、プログラムのメインブランチに返されます。フィボナッチ数列の4番目の要素は3つです：1 1 23。

さまざまなオリンピアードでこのような問題が発生することがよくありますが、一見すると、簡単な列挙で解決できるようです。しかし、数を数えるとオプション、すると、このアプローチの非効率性がすぐにわかります。たとえば、以下の単純な再帰関数は、すでに30番目のフィボナッチ数でかなりのリソースを消費しますが、オリンピアズでは、解決時間は1〜5秒に制限されることがよくあります。

int fibo（int n）（if（n == 1 || n == 2）（return 1;）else（return fibo（n-1）+ fibo（n-2）;））

なぜこれが起こるのか考えてみましょう。たとえば、fibo（30）を計算するには、最初にfibo（29）とfibo（28）を計算します。しかし同時に、私たちのプログラムはそのfibo（28）を「忘れる」 すでに計算済み fibo（29）を探すとき。

この正面からのアプローチの主な間違いは、関数の引数の同じ値が何度も計算されることです-これらはかなりリソースを消費する操作です。動的計画法は、反復計算を取り除くのに役立ちます。これは、タスクを一般的なサブタスクと反復サブタスクに分割し、それぞれが1回だけ解決される場合の手法です。これにより、プログラムの効率が大幅に向上します。この方法については、で詳しく説明します。他の問題を解決する例もあります。

関数を改善する最も簡単な方法は、すでに計算した値を覚えておくことです。これを行うには、追加の配列を導入する必要があります。これは、計算の一種の「キャッシュ」として機能します。新しい値を計算する前に、以前に計算されたかどうかを確認します。計算した場合は、配列から準備完了値を取得します。計算しなかった場合は、前の値に基づいて計算し、将来のために覚えておく必要があります。

Intキャッシュ; int fibo（int n）（if（cache [n] == 0）（if（n == 1 || n == 2）（cache [n] = 1;）else（cache [n] = fibo（n --1）+ fibo（n --2）;））return cache [n];）

このタスクでは、N番目の値を計算するために（N-1）番目の値が必要であることが保証されているため、反復形式で数式を書き直すことは難しくありません。配列に到達するまで、配列を行に入力するだけです。目的のセル：

<= n; i++) { cache[i] = cache + cache; } cout << cache;

これで、F（N）の値を計算すると、F（N-3）の値がすでに保証されていることがわかります。 一度もない必要ありません。つまり、F（N-1）とF（N-2）の2つの値だけをメモリに保存するだけで十分です。さらに、F（N）を計算するとすぐに、F（N-2）を格納することはすべての意味を失います。これらの考えをコードの形で書いてみましょう。

//以前の2つの値：int cache1 = 1; int cache2 = 1; //新しい値intcache3; for（int i = 2; i<= n; i++) { cache3 = cache1 + cache2; //Вычисляем новое значение //Абстрактный cache4 будет равен cache3+cache2 //Значит cache1 нам уже не нужен?.. //Отлично, значит cache1 -- то значение, которое потеряет актуальность на следующей итерации. //cache5 = cache4 - cache3 =>反復により、cache2はその関連性を失います。 cache1になります//つまり、cache1 --f（n-2）、cache2 --f（n-1）、cache3 --f（n）になります。 // N = n + 1（次の反復で計算する数）とします。次に、n-2 = N-3、n-1 = N-2、n = N-1です。 //新しい現実に従って、変数の値を書き換えます：cache1 = cache2; cache2 = cache3; ）切る<< cache3;

経験豊富なプログラマーは、cache3が使用されることはなく（すぐにcache2に書き込まれる）、1つの式を使用して反復全体を書き換えることができるため、上記のコードは一般にナンセンスであることを理解しています。

cache = 1; cache = 1; for（int i = 2; i<= n; i++) { cache = cache + cache; //При i=2 устареет 0-й элемент //При i=3 в 0 будет свежий элемент (обновили его на предыдущей итерации), а в 1 -- ещё старый //При i=4 последним элементом мы обновляли cache, значит ненужное старьё сейчас в cache //Интуитивно понятно, что так будет продолжаться и дальше } cout << cache;

モジュロマジックがどのように機能するかを理解できない場合、またはより明白でない式を見たい場合は、別の解決策があります。

int x = 1; int y = 1; for（int i = 2; i< n; i++) { y = x + y; x = y - x; } cout << "Число Фибоначчи: " << y;

このプログラムの実行を追跡してみてください。アルゴリズムが正しいことを確信できます。

P.S. 一般に、反復や再帰を必要としないフィボナッチ数を計算するための単一の式があります。

Const double SQRT5 = sqrt（5）; const double PHI =（SQRT5 + 1）/ 2; int fibo（int n）（return int（pow（PHI、n）/ SQRT5 + 0.5）;）

ただし、ご想像のとおり、整数以外の数値の累乗を計算するコストは、誤差と同様に非常に大きいという問題があります。

密閉する