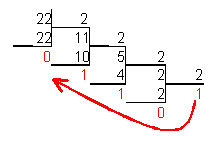
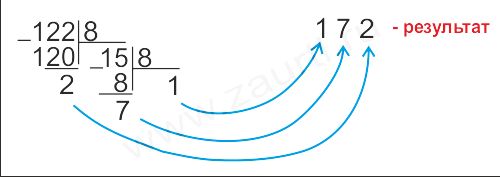
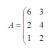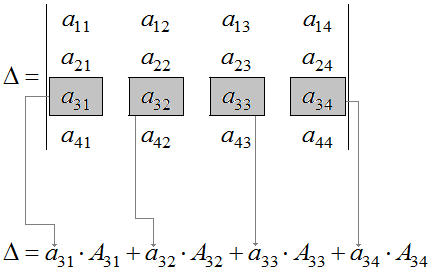Ηλεκτρονική αποσύνθεση προσδιορισμού. Ανάλυση γραμμής

Για τον προσδιοριστή της τέταρτης και της υψηλότερης σειράς, χρησιμοποιούνται συνήθως άλλες μέθοδοι υπολογισμού από τη χρήση έτοιμων τύπων όπως για τον υπολογισμό των καθοριστικών παραγόντων της δεύτερης και της τρίτης παραγγελίας. Μία από τις μεθόδους υπολογισμού των καθοριστικών παραγόντων υψηλότερης τάξης είναι η χρήση του αποτελέσματος από το θεώρημα Laplace (το ίδιο το θεώρημα μπορεί να βρεθεί, για παράδειγμα, στο βιβλίο του A.G. Kurosh "Μάθημα στην ανώτερη άλγεβρα"). Αυτό το πόρισμα μας επιτρέπει να αποσυνθέσουμε τον καθοριστικό παράγοντα σε στοιχεία μιας σειράς ή στήλης. Επιπλέον, ο υπολογισμός του καθοριστικού παράγοντα της nης τάξης μειώνεται στον υπολογισμό των n καθοριστών της (n-1) τάξης. Γι 'αυτό ένας τέτοιος μετασχηματισμός ονομάζεται μείωση της τάξης του καθοριστικού παράγοντα. Για παράδειγμα, ο υπολογισμός ενός καθοριστικού παράγοντα τέταρτης τάξης μειώνει την εύρεση τεσσάρων παραγόντων προσδιορισμού τρίτης τάξης.

Υποθέστε ότι μας δίνεται μια τετραγωνική μήτρα n-τάξης, δηλ. (A) (11) & a_ (12) & \\ ldots & a_ (1n) \\\\ a_ (21) & a_ (22) & \\ ldots & a_ (2n) \\\\ \\ ldots & \\ ldots & \\ ldots & \\ ldots \\\\ a_ (n1) & a_ (n2) & \\ ldots & a_ (nn) \\\\ \\ end (πίνακας) \\ δεξιά) $. Ο καθοριστικός παράγοντας αυτής της μήτρας μπορεί να υπολογιστεί με την επέκτασή της κατά σειρά ή στήλη.

Διορθώνουμε μια σειρά του οποίου ο αριθμός είναι $ i $. Στη συνέχεια, ο καθοριστικός παράγοντας της μήτρας $ A_ (n \\ times n) $ μπορεί να επεκταθεί στην επιλεγμένη i-th γραμμή χρησιμοποιώντας τον ακόλουθο τύπο:

  \\ (α) (i1) A_ (i1) + a_ (i2) A_ (i2) + \\ ldots + a_ (in) A_ (in) \\ end (εξίσωση)

$ A_ (ij) $ δηλώνει το αλγεβρικό συμπλήρωμα του στοιχείου $ a_ (ij) $. Για περισσότερες πληροφορίες σχετικά με αυτήν την ιδέα, σας συνιστώ να κοιτάξετε το θέμα Αλγεβρικές προσθήκες και ανηλίκους. Η συμβολοσειρά $ a_ (ij) $ δηλώνει ένα στοιχείο μιας μήτρας ή καθοριστικού παράγοντα που βρίσκεται στη διασταύρωση της iης σειράς της στήλης jth. Για περισσότερες πληροφορίες, μπορείτε να δείτε το θέμα του Matrix. Τύποι πινάκων. Βασικοί όροι.

Ας υποθέσουμε ότι θέλουμε να βρούμε το ποσό $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $. Ποια φράση μπορεί να περιγράψει την καταχώρηση $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $; Μπορούμε να πούμε αυτό: αυτό είναι το άθροισμα ενός τετραγώνου, δύο τετραγώνων, τριών τετραγώνων, τετραγώνων και τετραγώνων. Αλλά μπορούμε να πούμε ότι είναι μικρότερο: αυτό είναι το άθροισμα των τετραγώνων των ακεραίων από 1 έως 5. Για να εκφράσουμε το ποσό πιο σύντομα, χρησιμοποιήστε το γράμμα $ \\ sum $ (αυτό είναι το ελληνικό γράμμα "sigma").

Αντί του $ 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2 $, μπορούμε να χρησιμοποιήσουμε την ακόλουθη καταχώρηση: $ \\ sum \\ limits_ (i \u003d 1) ^. Το γράμμα $ i $ αναφέρεται ως δείκτη αθροίσματος, και οι αριθμοί 1 (αρχική τιμή $ i $) και 5 (τελική τιμή $ i $) καλούνται κατώτατα και ανώτερα όρια αθροίσματος  αναλόγως.

Έχουμε αποκρυπτογραφήσει λεπτομερώς την είσοδο $ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 $. Αν $ i \u003d 1 $, τότε $ i ^ 2 \u003d 1 ^ 2 $, ο πρώτος όρος αυτού του ποσού θα είναι ο αριθμός $ 1 ^ 2 $:

  $$ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 \u003d 1 ^ 2 + \\ ldots $$

Ο επόμενος ακέραιος μετά την ενότητα είναι ένας, έτσι αντικαθιστώντας το $ i \u003d 2 $, παίρνουμε: $ i ^ 2 \u003d 2 ^ 2 $. Το ποσό θα είναι τώρα έτσι:

  $$ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 \u003d 1 ^ 2 + 2 ^ 2 + \\ ldots $$

Μετά από δύο, ο επόμενος αριθμός είναι τριπλός, επομένως αντικαθιστώντας το $ i \u003d 3 $ θα έχουμε: $ i ^ 2 \u003d 3 ^ 2 $. Και το ποσό θα λάβει τη μορφή:

  $$ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 \u003d 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + \\ ldots $$

Παραμένει να αντικαταστήσουμε μόνο δύο αριθμούς: 4 και 5. Εάν αντικαταστήσουμε $ i \u003d 4 $, τότε $ i ^ 2 \u003d 4 ^ 2 $, και αν αντικαταστήσουμε $ i \u003d 5 $, τότε $ i ^ 2 \u003d 5 ^ 2 $. Οι τιμές του $ i $ έχουν φτάσει στο ανώτατο όριο της άθροσης · \u200b\u200bεπομένως, ο όρος $ 5 ^ 2 $ θα είναι ο τελευταίος. Έτσι, το τελικό ποσό τώρα είναι:

  $$ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 \u003d 1 ^ 2 + 2 ^ 2 + 3 ^ 2 + 4 ^ 2 + 5 ^ 2. $$

Αυτό το ποσό μπορεί να υπολογιστεί προσθέτοντας τους αριθμούς: $ \\ sum \\ limits_ (i \u003d 1) ^ (5) i ^ 2 \u003d 55 $.

Για πρακτική, προσπαθήστε να γράψετε και να υπολογίσετε το ακόλουθο ποσό: $ \\ sum \\ limits_ (k \u003d 3) ^ (8) (5k + 2) $. Ο δείκτης άθροισης εδώ είναι το γράμμα $ k $, το κατώτατο όριο του αθροίσματος είναι 3 και το ανώτερο όριο του αθροίσματος είναι 8.

  $$ \\ sum \\ limits_ (k \u003d 3) ^ (8) (5k + 2) \u003d 17 + 22 + 27 + 32 + 37 + 42 \u003d 177. $$

Ένα ανάλογο του τύπου (1) υπάρχει για στήλες. Ο τύπος για την αποσύνθεση του καθοριστικού παράγοντα στη στήλη jth έχει ως εξής:

  \\ (α) (1) + A_ (2j) A_ (2j) + \\ ldots + a_ (nj) A_ (nj) \\ τέλος (εξίσωση)

Οι κανόνες που εκφράζονται με τους τύπους (1) και (2) μπορούν να διαμορφωθούν ως εξής: ο προσδιοριστής είναι ίσος με το άθροισμα των προϊόντων των στοιχείων μιας σειράς ή στήλης με το αλγεβρικό συμπλήρωμα αυτών των στοιχείων. Για λόγους σαφήνειας, θεωρήστε τον καθοριστικό παράγοντα τέταρτης τάξης, γραμμένο σε γενική μορφή:

  $$ \\ Delta \u003d \\ αριστερά | \\ a (21) & a_ (22) & a_ (23) & a_ (24) \\\\ (a) α_ (31) & α_ (32) & α_ (33) & a_ (34) \\\\ a_ (41) & a_ (42) & a_ (43) & a_ (44) \\\\ \\ end | $$

Επιλέγουμε μια αυθαίρετη στήλη σε αυτόν τον καθοριστικό παράγοντα. Πάρτε, για παράδειγμα, τον αριθμό στήλης 4. Γράφουμε τον τύπο για την αποσύνθεση του προσδιοριστή στην επιλεγμένη τέταρτη στήλη:

Ομοίως, επιλέγοντας, για παράδειγμα, την τρίτη σειρά, αποκτάμε την επέκταση σε αυτή τη σειρά:

Παράδειγμα Νο. 1

Υπολογίστε τον καθοριστικό παράγοντα του μήκους $ A \u003d \\ left (\\ begin (array) (ccc) 5 & -4 & 3 \\\\ 7 & 2 & -1 \\\\ 9 & 0 & 4 \\ end (array) στην πρώτη σειρά και στη δεύτερη στήλη.

Πρέπει να υπολογίσουμε τον καθοριστικό παράγοντα τρίτης τάξης $ \\ Delta A \u003d \\ left | \\ begin (array) (ccc) 5 & -4 & 3 \\\\ 7 & 2 & -1 \\\\ 9 & 0 & 4 \\ end (array) \\ right | $. Για να το αναπτύξετε στην πρώτη γραμμή πρέπει να χρησιμοποιήσετε τον τύπο. Γράφουμε αυτή την αποσύνθεση σε γενική μορφή:

  (11) \\ cdot A_ (11) + α_ (12) \\ cdot A_ (12) + α_ (13) \\ cdot A_ (13). $$

Για το matrix μας, $ a_ (11) \u003d 5 $, $ a_ (12) \u003d - 4 $, $ a_ (13) \u003d 3 $. Για να υπολογίσουμε τα αλγεβρικά συμπληρώματα $ A_ (11) $, $ A_ (12) $, $ A_ (13) $ θα χρησιμοποιήσουμε τον τύπο αριθ. 1 από το θέμα που αφιερώνεται. Έτσι, τα επιθυμητά αλγεβρικά συμπληρώματα έχουν ως εξής:

  \\ begin (ευθυγραμμισμένο) & A_ (11) \u003d (- 1) ^ 2 \\ cdot \\ left | \\ begin (array) (cc) 2 & -1 \\\\ 0 & 4 \\ end (array) \\ right | \u003d 2 \\ cdot 4 - (- 1) \\ cdot 0 \u003d -1) ^ 3 \\ cdot \\ αριστερά | \\ begin (array) (cc) 7 & -1 \\\\ 9 & 4 \\ end (array) \\ right | \u003d - (7 \\ cdot 4 - 13) \u003d (- 1) ^ 4 \\ cdot \\ αριστερά | \\ begin (array) (cc) 7 & 2 \\\\ 9 & 0 \\ τέλος (πίνακας) \\ right | \u003d 7 \\ cdot 0-2 \\ cdot 9 \u003d -18. \\ end (ευθυγραμμισμένο)

Πώς βρήκαμε αλγεβρικές συμπληρώσεις; show \\ hide

Αντικαθιστώντας όλες τις τιμές που βρέθηκαν στον παραπάνω τύπο, παίρνουμε:

  (3) + α_ (13) \\ cdot A_ (13) \u003d 5 \\ cdot (8) + (- 4) \\ cdot (-37) +3 \\ cdot (-18) \u003d 134. $$

Όπως μπορείτε να δείτε, μειώσαμε τη διαδικασία εύρεσης του προσδιοριστή τρίτης τάξης στον υπολογισμό των τιμών των τριών προσδιοριστών δεύτερης τάξης. Με άλλα λόγια, έχουμε μειώσει τη σειρά του αρχικού προσδιοριστικού.

Συνήθως, σε τέτοιες απλές περιπτώσεις, δεν περιγράφουν λεπτομερώς τη λύση, χωριστά βρίσκοντας αλγεβρικά συμπληρώματα και στη συνέχεια αντικαθιστώντας τους με τον τύπο για τον υπολογισμό του καθοριστικού παράγοντα. Τις περισσότερες φορές, απλά συνεχίζουν να καταγράφουν τον γενικό τύπο, μέχρις ότου ληφθεί μια απάντηση. Έτσι θα αρχίσουμε να καθορίζουμε τον προσδιοριστικό παράγοντα στη δεύτερη στήλη.

Συνεπώς, προχωρούμε στην αποσύνθεση του καθοριστικού παράγοντα στη δεύτερη στήλη. Δεν θα εκτελέσουμε βοηθητικούς υπολογισμούς, απλά συνεχίζουμε τη φόρμουλα έως ότου λάβουμε μια απάντηση. Σημειώστε ότι στη δεύτερη στήλη, ένα στοιχείο είναι μηδέν, δηλ. $ a_ (32) \u003d 0 $. Αυτό υποδηλώνει ότι ο όρος $ a_ (32) \\ cdot A_ (32) \u003d 0 \\ cdot A_ (23) \u003d 0 $. Χρησιμοποιώντας τον τύπο για την επέκταση στη δεύτερη στήλη, λαμβάνουμε:

  (32) \\ cdot A_ (32) \u003d - 4 \\ cdot (-1) \\ cdot \\ a \\ (\\ αριστερά | \\ begin (array) (cc) 7 & -1 \\\\ 9 & 4 \\ end (array) \\ right | + 2 \\ cdot \\ left | \\ begin (array) (cc) 5 & 3 \\\\ 9 & 4 \\ τέλος (πίνακας) \\ right | \u003d 4 \\ cdot 37 + 2 \\ cdot (-7) \u003d 134. $$

Η απάντηση ελήφθη. Φυσικά, το αποτέλεσμα της επέκτασης στη δεύτερη στήλη συνέπεσε με το αποτέλεσμα της επέκτασης στην πρώτη σειρά, διότι βγήκαμε τον ίδιο καθοριστή. Σημειώστε ότι κατά την επέκταση κατά μήκος της δεύτερης στήλης, κάναμε λιγότερους υπολογισμούς, καθώς ένα στοιχείο της δεύτερης στήλης ήταν ίσο με το μηδέν. Με βάση τέτοιες σκέψεις προσπαθεί να επιλέξει τη στήλη ή τη σειρά που περιέχει περισσότερα μηδενικά για αποσύνθεση.

Η απάντηση: $ \\ Δέλτα Α \u003d 134 $.

Παράδειγμα αριθ. 2

Υπολογίστε τον καθοριστικό παράγοντα της μήτρας $ A \u003d \\ left (\\ begin (array) (cccc) -1 & 3 & 2 & -3 \\\\ 4 & -2 & 5 & 1 \\\\ -5 & 0 & -4 & 0 \\\\ 9 & 7 & 8 & -7 \\ end (array) \\ right) $, χρησιμοποιώντας την επέκταση της επιλεγμένης σειράς ή στήλης.

Για την αποσύνθεση, είναι πολύ ωφέλιμο να επιλέξετε τη σειρά ή τη στήλη που περιέχει τα πιο μηδενικά. Φυσικά, στην περίπτωση αυτή είναι λογικό να αναφερθεί στην τρίτη γραμμή, αφού περιέχει δύο στοιχεία ίσα με το μηδέν. Χρησιμοποιώντας τον τύπο, γράφουμε την επέκταση του καθοριστικού παράγοντα στην τρίτη γραμμή:

  (32) + a_ (33) \\ cdot A_ (33) + a_ (34) \\ cdot A_ (34). $$

Δεδομένου ότι $ a_ (31) \u003d - 5 $, $ a_ (32) \u003d 0 $, $ a_ (33) \u003d - 4 $, $ a_ (34) \u003d 0 $,

  $$ \\ Delta Α \u003d -5 \\ cdot Α_ (31) -4 \\ cdot Α_ (33). $$

Επιστρέφουμε στα αλγεβρικά συμπληρώματα $ A_ (31) $ και $ A_ (33) $. Για να τα υπολογίσουμε, θα χρησιμοποιήσουμε τον τύπο Νο 2 από το θέμα που αφιερώνεται στους καθοριστικούς παράγοντες της δεύτερης και της τρίτης παραγγελίας (στην ίδια ενότητα υπάρχουν λεπτομερή παραδείγματα της εφαρμογής αυτού του τύπου).

  \\ begin (ευθυγραμμισμένο) & A_ (31) \u003d (- 1) ^ 4 \\ cdot \\ left | \\ begin (array) (ccc) 3 & 2 & -3 \\\\ -2 & 5 & 1 \\\\ 7 & 8 & -7 \\ end (array) \\ right | \u003d 10; \\\\ & A_ (33) -1) ^ 6 \\ cdot \\ αριστερά | \\ begin (array) (ccc) -1 & 3 & -3 \\\\ 4 & -2 & 1 \\\\ 9 & 7 & -7 \\ end (array) \\ right | \u003d -34. \\ end (ευθυγραμμισμένο)

Αντικαθιστώντας τα ληφθέντα δεδομένα στον τύπο για τον καθοριστικό παράγοντα, θα έχουμε:

  $$ \\ Delta Α \u003d -5 \\ cdot Α_ (31) -4 \\ cdot A_ (33) \u003d - 5 \\ cdot 10-4 \\ cdot (-34) \u003d 86. $$

Κατ 'αρχήν, ολόκληρη η λύση μπορεί να γραφτεί σε μία γραμμή. Εάν παραλείψετε όλες τις εξηγήσεις και τους ενδιάμεσους υπολογισμούς, τότε η καταγραφή της λύσης θα είναι η εξής:

  (33) + a_ (34) \\ cdot A_ (34) \u003d a_ (32) \\ cdot A_ (32) \\\\ \u003d -5 \\ cdot (-1) ^ 4 \\ cdot \\ αριστερά | \\ begin (array) (ccc) 3 & 2 & -3 \\\\ -2 & 5 & 1 \\\\ 7 & 8 & -7 \\ end (array) \\ right | -4 \\ cdot \\ left \\ \\ begin (array) (ccc) -1 & 3 & -3 \\\\ 4 & -2 & 1 \\\\ 9 & 7 & -7 \\ τέλος (array) \\ right | \u003d -5 \\ cdot 10-4 \\ cdot -34) \u003d 86. $$

Η απάντηση: $ \\ Delta Α \u003d 86 $.

Διάλεξη 1.

Ο ορισμός του πίνακα. Οι παράγοντες προσδιορισμού της δεύτερης και τρίτης τάξης, οι κυριότερες ιδιότητές τους. Άτομα και αλγεβρικά συμπληρώματα, η επέκταση του καθοριστικού παράγοντα σε μια σειρά (στήλη). Μέθοδοι υπολογισμού των καθοριστικών παραγόντων. Η έννοια του καθοριστικού παράγοντα n η τάξη.

Ορισμός 1.1. Matrix  ονομάζεται ορθογώνιος πίνακας αριθμών.

Ονομασίες: Α - μήτρα, - στοιχείο μήτρας, αριθμός σειράς στον οποίο βρίσκεται αυτό το στοιχείο, αριθμός της αντίστοιχης στήλης.m   - τον αριθμό των σειρών της μήτρας,n   Είναι ο αριθμός των στηλών του.

Ορισμός 1.2. Οι αριθμοί m και n   καλούνται διαστάσεις  μήτρες.

Ορισμός 1.3.  Ο πίνακας καλείται τετράγωνοεάνm \u003d n. Αριθμός n   σε αυτή την περίπτωση που ονομάζεται τάξη  τετραγωνική μήτρα.

Κάθε τετραγωνική μήτρα μπορεί να συσχετιστεί με έναν αριθμό καθορισμένο μοναδικά χρησιμοποιώντας όλα τα στοιχεία της μήτρας. Αυτός ο αριθμός ονομάζεται καθοριστικός παράγοντας.

Ορισμός 1.4 .   Δεύτερο προσδιοριστικό   ονομάζεται ο αριθμός που λαμβάνεται χρησιμοποιώντας τα στοιχεία μιας τετραγωνικής μήτρας της 2ης τάξης ως εξής:

.

Σε αυτή την περίπτωση, το προϊόν των στοιχείων που βρίσκονται στη δεύτερη ή δευτερεύουσα διαγώνιο αφαιρείται από το προϊόν στοιχείων που στέκονται στη λεγόμενη κύρια διαγώνιο της μήτρας (που πηγαίνει από την άνω αριστερά στην κάτω δεξιά).

Παραδείγματα.

1. 2.

Ορισμός 1.5. Τρισδιάστατος προσδιοριστής  που ονομάζεται αριθμός, καθορίζεται χρησιμοποιώντας τα στοιχεία μιας τετραγωνικής μήτρας της 3ης τάξης ως εξής:

Παρατήρηση. Για να καταστεί ευκολότερη η ανάγνωση αυτού του τύπου, μπορείτε να χρησιμοποιήσετε τον λεγόμενο κανόνα τριγώνου. Αποτελείται από τα ακόλουθα: τα στοιχεία των οποίων τα έργα περιλαμβάνονται στον προσδιοριστή με το σύμβολο "+" είναι διατεταγμένα ως εξής:

σχηματίζοντας δύο τρίγωνα συμμετρικά ως προς την κύρια διαγώνιο. Τα στοιχεία των οποίων τα έργα περιλαμβάνονται στον προσδιοριστή με ένα σύμβολο "-" βρίσκονται με παρόμοιο τρόπο σε σχέση με την πλευρική διαγώνιο:

Παραδείγματα.

2.

Ορισμός 1. 6. Μεταφέρετε  οι μήτρες είναι μια λειτουργία, ως αποτέλεσμα των οποίων οι σειρές και οι στήλες εναλλάσσονται ενώ διατηρείται η σειρά τους. Το αποτέλεσμα είναι ένας πίνακας Α 'ονομάζεται μεταφερθείσε σχέση με το πλέγμα Ατα στοιχεία των οποίων συνδέονται με στοιχεία Α  την αναλογία α`   ij = ένα ji .

Οι κύριες ιδιότητες των καθοριστικών παραγόντων.

Διατυπώνουμε και αποδεικνύουμε τις κύριες ιδιότητες των καθοριστικών παραγόντων της 2ης και 3ης τάξης (η απόδειξη γίνεται για τους καθοριστικούς παράγοντες της 3ης τάξης).

Ιδιοκτησία 1.  Ο καθοριστικός παράγοντας δεν μεταβάλλεται κατά τη μεταφορά, δηλ.

Απόδειξη.

Παρατήρηση. Οι ακόλουθες ιδιότητες των καθοριστικών παραγόντων θα διατυπωθούν μόνο για τις χορδές. Επιπλέον, η ιδιότητα 1 υποδηλώνει ότι οι στήλες θα έχουν τις ίδιες ιδιότητες.

Ιδιοκτησία 2. Όταν πολλαπλασιάζονται τα στοιχεία της καθοριστικής γραμμής με ένα ορισμένο αριθμό, ολόκληρος ο προσδιοριστής πολλαπλασιάζεται με αυτόν τον αριθμό, δηλ.

.

Απόδειξη.

Ακίνητα 3.  Ο καθοριστικός παράγοντας που έχει μηδενική γραμμή είναι 0.

Η απόδειξη της ιδιότητας αυτής προκύπτει από την ιδιότητα 2 γιαk \u003d 0.

Ακίνητα 4.  Ο καθοριστικός παράγοντας που έχει δύο ίσες σειρές είναι 0.

Απόδειξη.

Ακίνητα 5. Ο προσδιοριστής, των οποίων οι δύο γραμμές είναι ανάλογες, είναι 0.

Η απόδειξη προκύπτει από τις ιδιότητες 2 και 4.

Ακίνητα 6. Όταν αναδιατάσσονται δύο γραμμές του προσδιοριστικού, πολλαπλασιάζεται επί -1.

Απόδειξη.

Ιδιοκτησία 7.

Η απόδειξη αυτής της ιδιότητας μπορεί να πραγματοποιηθεί ανεξάρτητα συγκρίνοντας τις τιμές της αριστεράς και της δεξιάς πλευράς της ισότητας που βρέθηκαν χρησιμοποιώντας τον ορισμό 1.5.

Ακίνητα 8.  Η τιμή του προσδιοριστικού δεν θα αλλάξει εάν τα αντίστοιχα στοιχεία μιας άλλης σειράς πολλαπλασιασμένα με τον ίδιο αριθμό προστεθούν στα στοιχεία μιας σειράς.

Η απόδειξη προκύπτει από τις ιδιότητες 7 και 5.

Η επέκταση του καθοριστικού παράγοντα σε μια σειρά.

Ορισμός 1. 7. Μικρά  ένα καθοριστικό στοιχείο είναι ένας καθοριστικός παράγοντας που λαμβάνεται από αυτό, διαγράφοντας τη σειρά και τη στήλη στην οποία βρίσκεται το επιλεγμένο στοιχείο.

Ονομασία: επιλεγμένο στοιχείο του προσδιοριστικού παράγοντα, το μικρό του.

Ένα παράδειγμα. Γιατί

Ορισμός 1. 8.Αλγεβρικό συμπλήρωμα  στοιχείο ενός προσδιοριστή ονομάζεται δευτερεύον του, αν το άθροισμα των δεικτών αυτού του στοιχείουi + j   υπάρχει ένας ζυγός αριθμός ή αριθμός αντίθετος προς το ανήλικα, εάνi + j   περίεργο, δηλ.

Εξετάστε έναν άλλο τρόπο υπολογισμού των καθοριστικών παραγόντων τρίτης τάξης - τη λεγόμενη επέκταση σε μια σειρά ή στήλη. Για να γίνει αυτό, αποδεικνύουμε το ακόλουθο θεώρημα:

Θεώρημα 1.1 . Ο προσδιοριστής είναι ίσος με το άθροισμα των προϊόντων των στοιχείων οποιασδήποτε σειράς ή στήλης με τις αλγεβρικές τους προσθήκες, δηλ.

όπουi \u003d 1,2,3.

Απόδειξη.

Ας αποδείξουμε το θεώρημα για την πρώτη σειρά του προσδιοριστικού παράγοντα, αφού για οποιαδήποτε άλλη σειρά ή στήλη μπορούμε να διεξαγάγουμε παρόμοια συλλογιστική και να έχουμε το ίδιο αποτέλεσμα.

Βρείτε το αλγεβρικό συμπλήρωμα στα στοιχεία της πρώτης σειράς:

Τότε

Επομένως, για να υπολογιστεί ο καθοριστικός παράγοντας, αρκεί να βρεθούν αλγεβρικές προσθήκες στα στοιχεία μίας σειράς ή στήλης και να υπολογιστεί το άθροισμα των προϊόντων τους από τα αντίστοιχα στοιχεία του προσδιοριστή.  έλαβε r ζευγών μεταβολών στοιχείων από το σύνολο 1,2, ...,n

Παρατήρηση 1. Οι ιδιότητες των καθοριστικών παραγόντων τρίτης τάξης ισχύουν επίσης για τους καθοριστικούς παράγοντεςnη τάξη.

Παρατήρηση 2. Στην πράξη, οι καθοριστικοί παράγοντες υψηλής τάξης υπολογίζονται με επέκταση κατά σειρά ή στήλη. Αυτό μας επιτρέπει να μειώσουμε τη σειρά των υπολογιζόμενων καθοριστών και τελικά να μειώσουμε το πρόβλημα στην εξεύρεση καθοριστικών παραγόντων τρίτης τάξης.

Ένα παράδειγμα. Υπολογίζουμε τον καθοριστικό παράγοντα τέταρτης τάξης χρησιμοποιώντας αποσύνθεση στην 2η στήλη. Για να γίνει αυτό, βρίσκουμε και:

Επομένως

Ορισμός 1. 7. Μικρά  ένα καθοριστικό στοιχείο είναι ένας καθοριστικός παράγοντας που λαμβάνεται από αυτό, διαγράφοντας τη σειρά και τη στήλη στην οποία βρίσκεται το επιλεγμένο στοιχείο.

Ονομασία: επιλεγμένο στοιχείο του προσδιοριστικού παράγοντα, το μικρό του.

Ένα παράδειγμα. Γιατί

Ορισμός 1. 8. Αλγεβρικό συμπλήρωμα  το στοιχείο του προσδιοριστικού ονομάζεται μικρότερο του, αν το άθροισμα των δεικτών αυτού του στοιχείου i + j είναι ένας ζυγός αριθμός ή αριθμός αντίθετος προς το ανήλικος, εάν το i + j είναι περιττό, δηλ.

Εξετάστε έναν άλλο τρόπο υπολογισμού των καθοριστικών παραγόντων τρίτης τάξης - τη λεγόμενη επέκταση σε μια σειρά ή στήλη. Για να γίνει αυτό, αποδεικνύουμε το ακόλουθο θεώρημα:

Θεώρημα 1.1. Ο προσδιοριστής είναι ίσος με το άθροισμα των προϊόντων των στοιχείων οποιασδήποτε σειράς ή στήλης με τις αλγεβρικές τους προσθήκες, δηλ.

  όπου i \u003d 1,2,3.

Απόδειξη.

Ας αποδείξουμε το θεώρημα για την πρώτη σειρά του προσδιοριστικού παράγοντα, αφού για οποιαδήποτε άλλη σειρά ή στήλη μπορούμε να διεξαγάγουμε παρόμοια συλλογιστική και να έχουμε το ίδιο αποτέλεσμα.

Βρείτε το αλγεβρικό συμπλήρωμα στα στοιχεία της πρώτης σειράς:

Έτσι, για να υπολογιστεί ο καθοριστικός παράγοντας, αρκεί να βρεθούν αλγεβρικές προσθήκες στα στοιχεία μίας σειράς ή στήλης και να υπολογιστεί το άθροισμα των προϊόντων τους από τα αντίστοιχα στοιχεία του προσδιοριστή.

Ένα παράδειγμα. Υπολογίζουμε τον καθοριστικό παράγοντα επεκτείνοντας την πρώτη στήλη. Σημειώστε ότι, στην περίπτωση αυτή, δεν είναι απαραίτητη η αναζήτηση, αφού, επομένως, θα βρούμε και   Επομένως

Προσδιοριστές υψηλότερων παραγγελιών.

Ορισμός 1. 9. Ο καθοριστικός παράγοντας της νια τάξης

υπάρχει ένα άθροισμα n! των μελών   κάθε ένα από τα οποία αντιστοιχεί σε ένα από n! παραταγμένες σειρές που λαμβάνονται με r ανά ζεύγη μεταβολές στοιχείων από το σύνολο 1,2, ..., n.

Παρατήρηση 1. Οι ιδιότητες των προσδιοριστών 3ης τάξης ισχύουν επίσης για καθοριστικούς παράγοντες n-τάξης.

Παρατήρηση 2. Στην πράξη, οι καθοριστικοί παράγοντες υψηλής τάξης υπολογίζονται με επέκταση κατά σειρά ή στήλη. Αυτό μας επιτρέπει να μειώσουμε τη σειρά των υπολογιζόμενων καθοριστών και τελικά να μειώσουμε το πρόβλημα στην εξεύρεση καθοριστικών παραγόντων τρίτης τάξης.

Ένα παράδειγμα. Υπολογίζουμε τον καθοριστικό παράγοντα τέταρτης τάξης   χρησιμοποιώντας αποσύνθεση στην 2η στήλη. Για να γίνει αυτό, βρίσκουμε και:

  Επομένως

Θεώρημα Laplace είναι ένα από τα θεωρήματα της γραμμικής άλγεβρας. Ονομάστηκε προς τιμήν του γαλλικού μαθηματικού Pierre-Simon Laplace (1749 - 1827), ο οποίος πιστώνεται με τη διατύπωση αυτού του θεώρημα το 1772, αν και μια ειδική περίπτωση αυτού του θεώρημα σχετικά με την επέκταση ενός προσδιοριστή σε μια σειρά (στήλη) ήταν γνωστή ακόμη και από Leibniz.

αναπλήρωση  ήσσονος σημασίας ορίζεται ως εξής:

Η ακόλουθη δήλωση είναι αληθής.

Ο αριθμός των ανηλίκων με τους οποίους το άθροισμα λαμβάνεται στο Θεώρημα Laplace είναι ίσος με τον αριθμό των τρόπων επιλογής των στηλών, δηλαδή ενός διωνυμικού συντελεστή.

Δεδομένου ότι οι σειρές και οι στήλες της μήτρας είναι ισοδύναμες σε σχέση με τις ιδιότητες του προσδιοριστή, το θεώρημα Laplace μπορεί επίσης να διαμορφωθεί για τις στήλες της μήτρας.

Αποσύνθεση του καθοριστικού παράγοντα από τη σειρά (στήλη) (Απόρροια 1)

Η ειδική περίπτωση του θεωρήματος Laplace είναι ευρέως γνωστή - η επέκταση του καθοριστικού παράγοντα σε μια σειρά ή μια στήλη. Μας επιτρέπει να αντιπροσωπεύουμε τον προσδιοριστή μιας τετραγωνικής μήτρας ως το άθροισμα των προϊόντων των στοιχείων οποιασδήποτε σειράς ή στήλης με τις αλγεβρικές τους προσθήκες.

Αφήνω να είναι μια τετράγωνη μήτρα μεγέθους. Αφήστε επίσης να δοθεί κάποιος αριθμός σειράς ή αριθμός στήλης της μήτρας. Στη συνέχεια, ο καθοριστικός παράγοντας μπορεί να υπολογιστεί με τους ακόλουθους τύπους.

Κατά την επίλυση προβλημάτων στα ανώτερα μαθηματικά, συχνά δημιουργείται η ανάγκη υπολογίζει τον προσδιοριστή μήτρας. Ο καθοριστικός παράγοντας μιας μήτρας εμφανίζεται στη γραμμική άλγεβρα, την αναλυτική γεωμετρία, τη μαθηματική ανάλυση και άλλους κλάδους των ανώτερων μαθηματικών. Έτσι, χωρίς την ικανότητα επίλυσης καθοριστικών παραγόντων απλά δεν μπορεί να κάνει. Επίσης, για τον αυτοέλεγχο, μπορείτε να κατεβάσετε τον υπολογιστή προσδιοριστών δωρεάν, δεν θα σας διδάξει πώς να λύσετε καθοριστικούς παράγοντες από μόνο του, αλλά είναι πολύ βολικό, αφού είναι πάντα ευεργετικό να γνωρίζετε τη σωστή απάντηση εκ των προτέρων!

Δεν θα δώσω έναν αυστηρό μαθηματικό ορισμό του καθοριστικού παράγοντα και, γενικά, θα προσπαθήσω να ελαχιστοποιήσω τη μαθηματική ορολογία · οι περισσότεροι αναγνώστες δεν θα αισθάνονται καλύτερα γι 'αυτό. Σκοπός αυτού του άρθρου είναι να σας διδάξει πώς να λύσετε τους προσδιοριστές δεύτερης, τρίτης και τέταρτης τάξης. Όλα τα υλικά παρουσιάζονται σε απλή και προσιτή μορφή και ακόμη και ένας πλήρης (άδειος) βραστήρας στα ανώτερα μαθηματικά, μετά από προσεκτική μελέτη του υλικού, θα μπορέσει να λύσει σωστά τους καθοριστικούς παράγοντες.

Στην πράξη, πιο συχνά μπορείτε να βρείτε έναν καθοριστικό παράγοντα δεύτερης τάξης, για παράδειγμα :, και έναν προσδιοριστή τρίτης τάξης, για παράδειγμα: .

Τέταρτος προσδιοριστικός παράγοντας   επίσης δεν αντίκες, και θα τον πλησιάσουμε στο τέλος του μαθήματος.

Ελπίζω ότι όλοι καταλαβαίνουν τα εξής:  Οι αριθμοί μέσα στον προσδιοριστή ζουν από μόνοι τους, και δεν υπάρχει λόγος για αφαίρεση! Δεν μπορείτε να ανταλλάξετε αριθμούς!

(Συγκεκριμένα, μπορείτε να εκτελέσετε ανά ζεύγη σειρές γραμμών ή στηλών του προσδιοριστικού παράγοντα με αλλαγή του σημείου του, αλλά συχνά αυτό δεν είναι απαραίτητο - δείτε το επόμενο μάθημα Ιδιότητες του καθοριστικού παράγοντα και μειώστε τη σειρά του)

Έτσι, εάν δοθεί κάποιος καθοριστικός παράγοντας, τότε μην αγγίζετε τίποτα μέσα σε αυτό!

Ονομασίες: Εάν δοθεί ένας πίνακας τότε προσδιορίζεται το αναγνωριστικό του. Πολύ συχνά το αναγνωριστικό σημειώνεται με λατινικό γράμμα ή ελληνικό.

1)  Τι σημαίνει επίλυση (εντοπισμός, αποκάλυψη) του καθοριστικού παράγοντα;  Για να υπολογίσετε τον καθοριστικό παράγοντα είναι να FIND ένα NUMBER. Τα ερωτηματικά στα παραπάνω παραδείγματα είναι εντελώς συνηθισμένοι αριθμοί.

2) Τώρα μένει να καταλάβουμε ΠΩΣ να βρούμε αυτόν τον αριθμό;  Για να γίνει αυτό, πρέπει να εφαρμόσετε ορισμένους κανόνες, τύπους και αλγόριθμους, οι οποίοι θα συζητηθούν τώρα.

Ας ξεκινήσουμε με τον καθοριστικό "δύο" έως "δύο":

Πρέπει να θυμόμαστε, τουλάχιστον για την περίοδο σπουδών ανώτατων μαθηματικών στο πανεπιστήμιο.

Ας εξετάσουμε αμέσως ένα παράδειγμα:

Έγινε. Το πιο σημαντικό, ΜΗ ΜΗΝ ΣΥΝΕΡΓΑΖΕΤΕ ΣΕ ΣΗΜΑΤΑ.

Τρισδιάστατος προσδιοριστής μήτρας  μπορεί να αποκαλυφθεί με 8 τρόπους, 2 απλοί και 6 κανονικοί.

Ας ξεκινήσουμε με δύο εύκολους τρόπους.

Παρόμοια με τον προσδιοριστή "δύο με δύο", ο προσδιοριστής "τρεις με τρεις" μπορεί να αποκαλυφθεί χρησιμοποιώντας τον τύπο:

Ο τύπος είναι μακρύς και είναι εύκολο να κάνει λάθος από την έλλειψη προσοχής. Πώς να αποφύγετε ενοχλητικές αποτυχίες; Γι 'αυτό, εφευρέθηκε μια δεύτερη μέθοδος υπολογισμού του προσδιοριστή, η οποία στην πραγματικότητα συμπίπτει με την πρώτη. Ονομάζεται η μέθοδος Sarryus ή η μέθοδος "παράλληλων λωρίδων".
   Η κατώτατη γραμμή είναι ότι η πρώτη και η δεύτερη στήλη αποδίδονται στο δεξιό μέρος του προσδιοριστή και οι γραμμές τραβιούνται προσεκτικά με ένα μολύβι:

   Οι πολλαπλασιαστές που βρίσκονται στις κόκκινες διαγώνιες συμπεριλαμβάνονται στον τύπο με ένα σύμβολο συν.
   Οι συντελεστές που βρίσκονται στις διαγώνιες "μπλε" συμπεριλαμβάνονται στον τύπο με το σημάδι μείον:

Ένα παράδειγμα:

Συγκρίνετε τις δύο λύσεις. Είναι εύκολο να δούμε ότι είναι ΕΝΑ ΚΑΙ ΟΜΟΙΟ, μόνο στη δεύτερη περίπτωση οι συντελεστές φόρμουλας είναι ελαφρώς αναδιαταγμένοι και, το σημαντικότερο, η πιθανότητα να γίνει λάθος είναι πολύ μικρότερη.

Τώρα εξετάστε έξι κανονικούς τρόπους για να υπολογίσετε τον καθοριστικό παράγοντα

Γιατί είναι φυσιολογικό; Επειδή στη συντριπτική πλειονότητα των περιπτώσεων απαιτείται να αποκαλυφθούν οι καθοριστικοί παράγοντες με αυτόν τον τρόπο.

Όπως παρατηρήσατε, ο καθοριστικός παράγοντας "τρεις με τρεις" έχει τρεις στήλες και τρεις σειρές.
   Ο καθοριστικός παράγοντας μπορεί να λυθεί ανοίγοντας τον από οποιαδήποτε σειρά ή από οποιαδήποτε στήλη.
   Έτσι, λαμβάνονται 6 μέθοδοι, ενώ σε όλες τις περιπτώσεις χρησιμοποιείται ίδιου τύπου  έναν αλγόριθμο.

Ο καθοριστικός παράγοντας μιας μήτρας είναι ίσος με το άθροισμα των προϊόντων των στοιχείων μιας σειράς (στήλης) με τις αντίστοιχες αλγεβρικές προσθήκες. Scary Όλα είναι πολύ πιο απλά, θα χρησιμοποιήσουμε μια μη επιστημονική, αλλά κατανοητή προσέγγιση, προσιτή ακόμη και σε ένα άτομο που απέχει πολύ από τα μαθηματικά.

Στο ακόλουθο παράδειγμα, θα αποκαλύψουμε τον καθοριστικό παράγοντα στην πρώτη γραμμή.
   Γι 'αυτό χρειαζόμαστε μια μήτρα σημείων :. Είναι εύκολο να παρατηρήσετε ότι τα σημάδια είναι κλιμακωτά.

Προσοχή! Η μήτρα των σημείων είναι η δική μου εφεύρεση. Αυτή η έννοια δεν είναι επιστημονική, δεν χρειάζεται να χρησιμοποιηθεί σε εργασίες τελικής επεξεργασίας, αλλά μόνο σας βοηθά να κατανοήσετε τον αλγόριθμο για τον υπολογισμό του καθοριστικού παράγοντα.

Θα δώσω πρώτα μια ολοκληρωμένη λύση. Και πάλι, παίρνουμε τον πειραματικό μας προσδιοριστή και πραγματοποιούμε τους υπολογισμούς:

Και το βασικό ερώτημα: ΠΩΣ να το αποκτήσετε από τον προκριματικό "τρία με τρία":
?

Έτσι, ο καθοριστικός παράγοντας "τρεις με τρεις" καταλήγει στη λύση τριών μικρών προσδιοριστών, ή όπως αποκαλούνται επίσης, MINOROV. Σας συνιστώ να θυμάστε τον όρο, ειδικά επειδή είναι αξέχαστο: ο μικρός είναι μικρός.

Δεδομένου ότι επιλέγεται η μέθοδος αποσύνθεσης του καθοριστή στην πρώτη γραμμή, προφανώς, τα πάντα περιστρέφονται γύρω της:

Τα στοιχεία συνήθως προβάλλονται από αριστερά προς τα δεξιά (ή από πάνω προς τα κάτω αν επιλεγεί μια στήλη)

Ας πάμε, πρώτα ασχολούμαστε με το πρώτο στοιχείο της γραμμής, δηλαδή με την ενότητα:

1) Από τη μήτρα των σημείων γράφουμε το αντίστοιχο σημάδι:

2) Στη συνέχεια γράφουμε το ίδιο το στοιχείο:

3) ΣΗΜΑΝΤΙΚΗ διασταύρωση της σειράς και της στήλης στην οποία βρίσκεται το πρώτο στοιχείο:

   Οι υπόλοιποι τέσσερις αριθμοί αποτελούν τον καθοριστικό παράγοντα "δύο με δύο", ο οποίος καλείται ΜΙΚΡΕΣ  αυτού του στοιχείου (μονάδα).

Περνάμε στο δεύτερο στοιχείο της γραμμής.

4) Από τη μήτρα των σημείων γράφουμε το αντίστοιχο σημάδι:

5) Στη συνέχεια γράφουμε το δεύτερο στοιχείο:

6) Διαγράψτε διανοητικά τη σειρά και τη στήλη στην οποία βρίσκεται το δεύτερο στοιχείο:

Λοιπόν, το τρίτο στοιχείο της πρώτης γραμμής. Δεν υπάρχει πρωτοτυπία:

7) Από τη μήτρα των σημείων γράφουμε το αντίστοιχο σημάδι:

8) Γράφουμε το τρίτο στοιχείο:

9) ΜΗΝΥΜΑΤΑ διασταυρώστε τη σειρά και τη στήλη στην οποία βρίσκεται το τρίτο στοιχείο:

   Οι υπόλοιποι τέσσερις αριθμοί είναι γραμμένοι σε ένα μικρό καθοριστικό παράγοντα.

Οι υπόλοιπες ενέργειες δεν είναι δύσκολες, αφού ήδη γνωρίζουμε πώς να μετρήσουμε τους δύο από τους δύο καθοριστικούς παράγοντες. ΜΗΝ ΜΗΝ ΣΥΝΔΕΣΕΤΕ ΣΕ ΣΗΜΑΤΑ!

Ομοίως, ο καθοριστικός παράγοντας μπορεί να επεκταθεί σε οποιαδήποτε σειρά ή σε οποιαδήποτε στήλη.  Φυσικά, και στις έξι περιπτώσεις η απάντηση είναι η ίδια.

Ο καθοριστικός παράγοντας "τέσσερα με τέσσερα" μπορεί να υπολογιστεί χρησιμοποιώντας τον ίδιο αλγόριθμο.
   Σε αυτή την περίπτωση, ο πίνακας σημείων θα αυξηθεί:

Στο ακόλουθο παράδειγμα, επέκτεινα τον προκριματικό στην τέταρτη στήλη:

Και πώς συνέβη, προσπαθήστε να το καταλάβετε μόνοι σας. Περισσότερες πληροφορίες θα γίνουν αργότερα. Αν κάποιος θέλει να λύσει τον καθοριστικό παράγοντα μέχρι το τέλος, η σωστή απάντηση είναι 18. Για την κατάρτιση, είναι καλύτερο να ανοίξουμε τον προσδιοριστή σε κάποια άλλη στήλη ή άλλη σειρά.

Η άσκηση, η αποκάλυψη, η πραγματοποίηση υπολογισμών είναι πολύ καλή και χρήσιμη. Αλλά πόσο χρόνο θα ξοδέψετε για τον μεγάλο καθοριστικό παράγοντα; Είναι δυνατόν με κάποιο τρόπο ταχύτερη και πιο αξιόπιστη; Προτείνω να εξοικειωθείτε με τις αποτελεσματικές μεθόδους υπολογισμού των καθοριστικών παραγόντων στο δεύτερο μάθημα - Ιδιότητες ενός καθοριστικού παράγοντα. Μειώστε τη σειρά του καθοριστικού παράγοντα.

ΠΡΟΣΟΧΗ!

α i, j

Προκριματικά

det (2A) \u003d det (2Ε) detA \u003d 0 2 0 (- 2) \u003d 23 (- 2) \u003d - 16. 0 0 2

(δ) Ομοίως,

det (- 3A) \u003d det (- 3E) detA \u003d (- 3) 3 (- 2) \u003d 54.

(ε) Πρώτα βρήκαμε τη μήτρα (Α-2Ε), και στη συνέχεια τον καθοριστικό της:

− 1 5

Α - 2 Ε \u003d

−1

−3

det (Α - 2Ε) \u003d 0 (- 1) (- 3) \u003d 0.

2.4. Υπολογισμός των καθοριστικών παραγόντων

Εδώ εξετάζουμε δύο μεθόδους για τον υπολογισμό των καθοριστικών παραγόντων. Η ουσία ενός από αυτά είναι να επεκτείνει τον καθοριστικό παράγοντα σε στοιχεία μιας σειράς ή στήλης, ως αποτέλεσμα του οποίου ο αρχικός προσδιοριστής της νια τάξης εκφράζεται με n καθοριστικούς παράγοντες μιας κατώτερης τάξης. Μια άλλη μέθοδος βασίζεται στις ιδιότητες των καθοριστικών παραγόντων και συνδέεται με τον μετασχηματισμό του καθοριστικού παράγοντα σε μια απλούστερη μορφή. Ο συνδυασμός των δύο μεθόδων παρέχει τον πιο αποτελεσματικό τρόπο για τον υπολογισμό των καθοριστικών παραγόντων.

2.4.1. Επέκταση του καθοριστικού παράγοντα σε στοιχεία μιας σειράς ή στήλης

Αρχικά εισάγουμε μερικές σημαντικές έννοιες για την επόμενη παρουσίαση.

Εξετάστε μια τετραγωνική μήτρα n-τάξης. Επιλέγουμε το στοιχείο i, jth αυτού του πίνακα και διαχωρίζουμε τη στήλη i και τη στήλη i. Ως αποτέλεσμα

παίρνουμε μια μήτρα (n-1) της τάξης, του οποίου ο προσδιοριστής ονομάζεται δευτερεύον στοιχείο του στοιχείου a i, j και συμβολίζεται με το σύμβολο M i, j.

Προκριματικά

Αλγεβρικό συμπλήρωμαA i, j του στοιχείου a i, j καθορίζεται από τον τύπο

Α i, j \u003d (- 1) i + j M i, j.

Είναι εύκολο να διαπιστώσουμε ότι το αλγεβρικό συμπλήρωμα του στοιχείου i, jth συμπίπτει με το δευτερεύον στοιχείο αυτού του στοιχείου εάν το άθροισμα των δεικτών που αριθμούν τη σειρά και τη στήλη του στοιχείου είναι ένας ζυγός αριθμός. Για περιττές τιμές του i + j, το αλγεβρικό συμπλήρωμα διαφέρει από το μικρότερο μόνο στο σημείο.

Το θεώρημα της επέκτασης του καθοριστικού παράγοντα στα στοιχεία της συμβολοσειράς.

Ο καθοριστικός παράγοντας της μήτρας Α είναι ίσος με το άθροισμα των προϊόντων των στοιχείων της σειράς με το αλγεβρικό τους συμπλήρωμα:

det A \u003d a i, 1A i, 1 + a i, 2A i, 2 + K + a i, n A i, n \u003d

\u003d Σ a i, jA i, j j \u003d 1

Απόδειξη: Εξ ορισμού, ο καθοριστικός παράγοντας της μήτρας Α είναι το άθροισμα

det A \u003d	(K 1, k 2, k, k n), k 1, k 1 a, k i K a n, k n (- 1)
	(k 1, k 2, K k i, K k n)

για όλες τις πιθανές μεταβολές δεικτών αρίθμησης των στηλών. Ας επιλέξουμε αυθαίρετα μια σειρά, για παράδειγμα, με

αριθμός i. Ένα από τα στοιχεία αυτής της γραμμής παρουσιάζεται σε κάθε εργασία a 1, k 1 a 2, k 2 K a i, k i K a n, k n. Επομένως, τα summands (*)

μπορούν να ανασυγκροτηθούν συνδυάζοντας στην πρώτη ομάδα εκείνες που περιέχουν το στοιχείο a i, 1 ως κοινό παράγοντα, στη δεύτερη ομάδα - μέλη,

Με άλλα λόγια, η έκφραση (*) μπορεί να αναπαρασταθεί ως ένας γραμμικός συνδυασμός των στοιχείων a i, j (j \u003d 1,2, L, n),

Προκριματικά

		(K 1, k 2, k, k n) \u003d k a (k 1)
det A \u003d Σ
j \u003d 1 (k1, k2, Kj, Κκ)
		(K 1, k 2, k, k n) \u003d k a 1 k 1 a 2 k 2 K a i 1 ki 1 a i 1 ki + 1 a n, kn (- 1)
\u003d Σ a i, j
j \u003d 1		(k 1, k 2, K j, K k n)
\u003d Σ i i, j A i, j \u003d a i, 1A i, 1 + a i, 2A i, 2 + K + a i, n A i, n,
j \u003d 1
	(1), k 1, k 1 a 2, k 2 L ai-1, ki-1 a i + 1, ki + 1 K a, kn (- 1) , kn).
Α i, j \u003d
(k 1, L, k i - 1, k i \u003d j, k i + 1, L, k n)
Αυτό δείχνουμε		Το i, j είναι αλγεβρικό	Επιπλέον
στοιχείο a i, j.
Εξετάστε την ισοτιμία της μετάθεσης (k 1, L, k i - 1, j, k i + 1, L, k n).
Πρώτον	i -1 μεταθέσεις του στοιχείου j με		γειτονικά

τα στοιχεία για να πάρουμε μια μετάθεση (j, k 1, L, k i - 1, k i + 1, L, k n).

Δεύτερον, στην προκύπτουσα μετάθεση, το στοιχείο j σχηματίζει j-1 αντιστροφές με άλλα στοιχεία.

Επομένως

(- 1) P (k 1, L, ki - 1, j, ki + 1, L, kn) 1, ki + 1, L, kn) \u003d

\u003d (- 1) i + j (- 1) P (k1, L, ki - 1, ki + 1, L, kn)

(1, L, ki - 1, ki + 1, L, kn) \u003d M i, j (k 1, L , ki - 1, ki + 1, L, kn)

αντιπροσωπεύει το δευτερεύον του στοιχείου a i, j.

Έτσι, A i, j \u003d (- 1) i + j M i, j, όπως απαιτείται.

Δεδομένου ότι det A \u003d det A T, το εξής ισχύει επίσης.

Το θεώρημα της επέκτασης του καθοριστικού παράγοντα στα στοιχεία της στήλης.

Ο προσδιοριστής της μήτρας Α είναι ίσος με το άθροισμα των προϊόντων των στοιχείων της στήλης με τις αλγεβρικές τους προσθήκες:

det A \u003d a 1, jA 1, j + a 2, jA 2, j + K + a n, j A n, j

\u003d Σ a i, jA i, j

i \u003d 1

Προκριματικά

Τα θεωρήματα αποσύνθεσης του καθοριστικού παράγοντα είναι σημαντικά στη θεωρητική έρευνα. Δηλώνουν ότι το πρόβλημα του υπολογισμού του καθορισμού της n-τάξης μειώνεται στο πρόβλημα του υπολογισμού των n καθοριστών της (n-1) τάξης.

Παραδείγματα:

1) Υπολογίστε τον προσδιοριστή μιας αυθαίρετης μήτρας A \u003d || a ij || τρίτο

αποσύνθεση στοιχείου

i) την πρώτη γραμμή ·

(ii) τη δεύτερη στήλη.

Λύση:

-Α

det A \u003d

Α 11 (α 22α 33-α 23α 32) - α 12 (α 21α 33- a 23a 31) + a 13 (a 21a 32- a 22a 31)

Α 11α 22α 33+ α 12α 23α 31+ α 13α 21α 32- α 11α 23α 32- α 12α 21α 33-α 13α 22α 31,

-Α

det A \u003d

\u003d -Α

\u003d α 12 (a 12a 33- a 23a 31) + a 22 (a 11a 33- a 13a 31) - a 32 (a 11a 23- a 13a 21)

Α 11α 22α 33+ α 12a 23a 31+ α 13a 21a 32- a 11a 23a 32- a 12a 21a 33- a 13a 22a 31.

Τα αποτελέσματα που λαμβάνονται με διάφορες μεθόδους είναι πανομοιότυπα.

Υπολογίστε τον καθοριστικό παράγοντα

−5

αποσύνθεση

−3

(i) την πρώτη γραμμή,

(ii) τη δεύτερη στήλη.

Λύση:

Αποσυντίθεται ο καθοριστικός παράγοντας σε στοιχεία της πρώτης σειράς

−5

− (− 5)

−3

−3

− 3 7

2 4 5 + 5 1 5+ 3(7+ 12)= 122.

(ϋ) Το ίδιο αποτέλεσμα λαμβάνεται όταν ο καθοριστικός παράγοντας αποσυντίθεται στα στοιχεία της δεύτερης στήλης:

Προκριματικά

	−5
			= −(−5)					−7
−3				−3			− 3 5

5(5 + 0)+ 4 (10+ 9)− 7(0− 3)= 122.

2.4.2. Υπολογισμός των προσδιοριστών με τη στοιχειώδη μέθοδο

μετασχηματισμούς

Οι στοιχειώδεις μετασχηματισμοί σημαίνουν τις ακόλουθες λειτουργίες.

Λόγω της ισότητας των σειρών και των στηλών του προσδιοριστικού στοιχείου, τέτοιες διαδικασίες εφαρμόζονται πλήρως στις στήλες.

Η ιδέα της μεθόδου είναι να χρησιμοποιήσουμε τους στοιχειώδεις μετασχηματισμούς των σειρών και των στηλών για να φέρουμε τον προσδιοριστή σε μια τριγωνική μορφή, η οποία λύνει το πρόβλημα του υπολογισμού του.

Κάποιος μπορεί να δράσει λίγο διαφορετικά: χρησιμοποιώντας στοιχειώδεις μετασχηματισμούς, πάρτε μια σειρά (ή στήλη) που περιέχει μόνο ένα μη μηδενικό στοιχείο και στη συνέχεια αποσυνθέστε τον προκύπτον καθοριστή σε στοιχεία αυτής της σειράς (στήλη). Μια τέτοια διαδικασία μειώνει τη σειρά του προσδιοριστή από μία μονάδα.

Παραδείγματα.

−4

−3

Υπολογίστε το det A μειώνοντας τη μήτρα στο

1) Ας Α \u003d

r 2+ 3 r 3

−3

↔r 3

→ r 3

−8

−5

Ο καθοριστικός παράγοντας μιας τριγωνικής μήτρας είναι ίσος με το προϊόν των διαγώνιων στοιχείων του:

det A \u003d - 1 8 9 \u003d - 72. 2) Υπολογίστε τον προσδιοριστή της μήτρας

			−2
				−1

Λύση: Αρχικά, μετασχηματίζουμε την πρώτη σειρά χρησιμοποιώντας στοιχειώδεις λειτουργίες στηλών, προσπαθώντας να πάρουμε τον μέγιστο δυνατό αριθμό μηδενικών σε αυτήν. Για το σκοπό αυτό, αφαιρέστε την πέμπτη στήλη, προηγουμένως πολλαπλασιασμένη με 5, από τη δεύτερη στήλη, και προσθέστε τη διπλασιασμένη δεύτερη στήλη στην τρίτη στήλη:

− 2 0

c → c- 5 c

−1

→ c 2

2 c 1

− 14

−1

det A \u003d

− 35

− 15

Τώρα αποσυνθέτουμε τον καθοριστικό παράγοντα στα στοιχεία της πρώτης γραμμής:

det A \u003d		− 14		−1
		− 35
		− 15