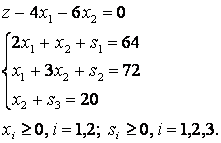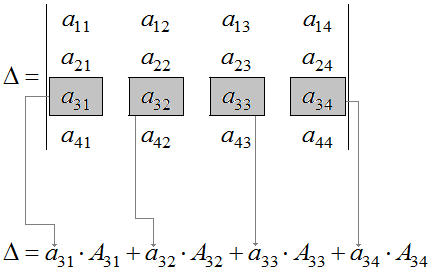Η λύση του προβλήματος παραγωγής με τη μέθοδο του πίνακα simplex. Απλή μέθοδος επίλυσης του zlp
Αν χρειαστεί να λύσετε το πρόβλημα του γραμμικού προγραμματισμού χρησιμοποιώντας πίνακες simplex, τότε η ηλεκτρονική υπηρεσία μας θα σας βοηθήσει πολύ. Η μέθοδος simplex περιλαμβάνει μια διαδοχική αναζήτηση όλων των κορυφών της περιοχής των αποδεκτών τιμών προκειμένου να βρεθεί η κορυφή όπου η συνάρτηση παίρνει μια ακραία τιμή. Στο πρώτο στάδιο, υπάρχει κάποια λύση που βελτιώνεται σε κάθε επόμενο βήμα. Μια τέτοια λύση ονομάζεται βασική. Ακολουθεί η ακολουθία ενεργειών κατά την επίλυση του προβλήματος γραμμικού προγραμματισμού με τη μέθοδο simplex:
Πρώτο βήμα. Στο συγκεντρωτικό πίνακα, πρώτα απ 'όλα, πρέπει να δείτε τη στήλη με ελεύθερα μέλη. Εάν υπάρχουν αρνητικά στοιχεία σε αυτό, τότε είναι απαραίτητο να γίνει η μετάβαση στο δεύτερο βήμα, αν όχι, τότε στο πέμπτο.
Δεύτερο βήμα. Στο δεύτερο βήμα, είναι απαραίτητο να καθορίσουμε ποια μεταβλητή να αποκλείσουμε από τη βάση και ποιες να συμπεριλάβουμε για να υπολογίσουμε εκ νέου τον απλό πίνακα. Για να το κάνετε αυτό, κοιτάξτε τη στήλη με ελεύθερα μέλη και βρείτε ένα αρνητικό στοιχείο σε αυτό. Μια γραμμή με αρνητικό στοιχείο θα ονομάζεται κορυφαία. Σε αυτό βρίσκουμε τη μέγιστη απόλυτη τιμή του αρνητικού στοιχείου, την αντίστοιχη στήλη - τον σκλάβο. Εάν μεταξύ των ελεύθερων μελών υπάρχουν αρνητικές τιμές, αλλά όχι στην αντίστοιχη σειρά, τότε ένας τέτοιος πίνακας δεν θα έχει λύσεις. Η μεταβλητή στην κύρια γραμμή που βρίσκεται στη στήλη των ελεύθερων μελών αποκλείεται από τη βάση και η μεταβλητή που αντιστοιχεί στην κύρια στήλη περιλαμβάνεται στη βάση.
Πίνακας 1.
| βασικές μεταβλητές | Τα ελεύθερα μέλη περιορίζονται | Μη βασικές μεταβλητές | |||||
| x 1 | x 2 | ... | x l | ... | x n | ||
| x n + 1 | β 1 | ένα 11 | ένα 12 | ... | ένα 1 λίτρο | ... | ένα 1n |
| x n + 2 | b 2 | 21 | ένα 22 | ... | ένα 2 λίτρο | ... | ένα 2n |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n + r | b2 | ένα r1 | ένα r2 | ... | ένα rl | ... | ένα rn |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| . | . | . | . | . | . | . | . |
| x n + m | b m | ένα m1 | ένα m2 | ... | ένα ml | ... | ένα mn |
| F (x) μέγ | F 0 | -c 1 | -c 2 | ... | -c 1 | ... | -c n |
Τρίτο βήμα. Στο τρίτο βήμα, υπολογίζουμε εκ νέου τον ολόκληρο πίνακα simplex σύμφωνα με τους ειδικούς τύπους, οι τύποι αυτοί μπορούν να φανούν χρήσιμοι.
Τέταρτο βήμα. Εάν μετά τον επανυπολογισμό στη στήλη των ελεύθερων όρων παραμένουν αρνητικά στοιχεία, τότε προχωράμε στο πρώτο βήμα, εάν δεν υπάρχουν, τότε στο πέμπτο.
Πέμπτο βήμα. Εάν έχετε φτάσει στο πέμπτο βήμα, τότε έχετε βρει μια λύση που είναι αποδεκτή. Ωστόσο, αυτό δεν σημαίνει ότι είναι βέλτιστο. Θα είναι βέλτιστη μόνο αν όλα τα στοιχεία της γραμμής F είναι θετικά. Εάν αυτό δεν συμβαίνει, τότε είναι απαραίτητο να βελτιωθεί η λύση, για την οποία βρίσκουμε την κύρια σειρά και τη στήλη για τον επόμενο επανυπολογισμό σύμφωνα με τον ακόλουθο αλγόριθμο. Αρχικά, βρίσκουμε τον ελάχιστο αρνητικό αριθμό στη συμβολοσειρά F, εξαιρουμένης της τιμής της συνάρτησης. Η στήλη με αυτόν τον αριθμό θα οδηγεί. Για να βρούμε την κορυφαία σειρά, βρίσκουμε την αναλογία του αντίστοιχου ελεύθερου όρου και του στοιχείου από την κορυφαία στήλη, υπό την προϋπόθεση ότι είναι θετικές. Ο ελάχιστος λόγος σάς επιτρέπει να ορίσετε μια κύρια γραμμή. Επαναλαμβάνουμε εκ νέου τον πίνακα σύμφωνα με τους τύπους, δηλ. μεταβείτε στο βήμα 3.
Μία από τις μεθόδους επίλυσης προβλημάτων βελτιστοποίησης ( συνήθως συνδέεται με την εξεύρεση ενός ελάχιστου ή μέγιστου) ο γραμμικός προγραμματισμός καλείται. Απλή μέθοδος περιλαμβάνει μια ολόκληρη ομάδα αλγορίθμων και μεθόδων για την επίλυση γραμμικών προβλημάτων προγραμματισμού. Μια από αυτές τις μεθόδους, η οποία προβλέπει την καταγραφή των πηγών δεδομένων και τη μετατροπή τους σε έναν ειδικό πίνακα, καλείται απλή μέθοδος πίνακα.
Σκεφτείτε τον αλγόριθμο της μεθόδου simplex πίνακα χρησιμοποιώντας το παράδειγμα μιας λύσης καθήκον παραγωγής, η οποία υποχωρεί στην εξεύρεση ενός σχεδίου παραγωγής που παρέχει το μέγιστο κέρδος.
Τα αρχικά δεδομένα του προβλήματος στη μέθοδο simplex
Η εταιρεία παράγει 4 τύπους προϊόντων, τα επεξεργάζεται σε 3 μηχανές.
Πρότυπα χρόνου (ελάχιστα / τεμ.) Για την επεξεργασία προϊόντων σε μηχανές που καθορίζονται από το πλέγμα Α:

Το ταμείο χρόνου λειτουργίας του μηχανήματος (ελάχιστο) καθορίζεται στον πίνακα Β:

Το κέρδος από την πώληση κάθε μονάδας του προϊόντος (ρούβλια / τεμ.) Δίνεται από τον πίνακα C:

Στόχος παραγωγής
Καταρτίστε ένα σχέδιο παραγωγής στο οποίο το κέρδος της επιχείρησης θα είναι το ανώτατο.
Η λύση του προβλήματος με τη μέθοδο simplex πίνακα
(1) Προσδιορίστε με X1, X2, X3, X4 τον προγραμματισμένο αριθμό προϊόντων κάθε τύπου. Τότε το επιθυμητό σχέδιο: ( Χ1, Χ2, Χ3, Χ4)
(2) Γράφουμε τους περιορισμούς του σχεδίου με τη μορφή ενός συστήματος εξισώσεων:

(3) Στη συνέχεια, το κέρδος στόχο:
Δηλαδή, το κέρδος από την εφαρμογή του σχεδίου παραγωγής πρέπει να είναι το μέγιστο.
(4) Για την επίλυση του προκύπτοντος προβλήματος από ένα υπό όρους άκρο, αντικαθιστούμε το σύστημα ανισοτήτων με ένα σύστημα γραμμικών εξισώσεων εισάγοντας επιπλέον μη αρνητικές μεταβλητές σε αυτό ( X5, Χ6, Χ7).

(5) Ακολουθήστε τα παρακάτω σχέδιο αναφοράς:
Χ1 \u003d 0, Χ2 \u003d 0, Χ3 \u003d 0, Χ4 \u003d 0, Χ5 \u003d 252, Χ6 \u003d 144, Χ7 \u003d 80
(6) Θα εισαγάγουμε τα δεδομένα στη διεύθυνση απλός πίνακας:

Στην τελευταία γραμμή εισάγουμε τους συντελεστές της αντικειμενικής συνάρτησης και της ίδιας της τιμής με το αντίθετο σημείο.
(7) Επιλέξτε στην τελευταία σειρά το μεγαλύτερο (modulo) αρνητικό αριθμό.
Υπολογίζουμε b \u003d N / Στοιχεία_της επιλεγμένης στήλης

Μεταξύ των υπολογισμένων τιμών του b, επιλέγουμε το μικρότερο.
Η τομή της επιλεγμένης στήλης και της σειράς θα μας δώσει ένα στοιχείο επίλυσης. Αλλάζουμε τη βάση για τη μεταβλητή που αντιστοιχεί στο στοιχείο επίλυσης ( X5 έως Χ1).

- Το ίδιο το στοιχείο διαχωρισμού μετατρέπεται σε 1.
- Για στοιχεία της γραμμής ανάλυσης - a ij (*) \u003d a ij / RE ( δηλαδή, διαιρούμε κάθε στοιχείο με την τιμή του στοιχείου επίλυσης και λαμβάνουμε νέα δεδομένα).
- Για στοιχεία στήλης ανάλυσης, απλώς ακυρώνονται.
- Τα υπόλοιπα στοιχεία του πίνακα αναπαρίστανται σύμφωνα με τον κανόνα ορθογωνίου.

a ij (*) \u003d a ij - (Α * Β / ΡΕ)
Όπως μπορείτε να δείτε, παίρνουμε το σημερινό επανυπολογισμένο κελί και το κελί με το στοιχείο επίλυσης. Δημιουργούν τις αντίθετες γωνίες του ορθογωνίου. Στη συνέχεια, πολλαπλασιάζουμε τις τιμές από τα κελιά των 2 άλλων γωνιών αυτού του ορθογωνίου. Αυτό το έργο ( Α * Β) διαιρέστε με το στοιχείο επίλυσης ( RE) Και αφαιρέστε από το τρέχον επανυπολογισμένο στοιχείο ( ένα ij) τι συνέβη. Έχουμε μια νέα αξία - ένα ij (*).

(9) Ελέγξτε ξανά την τελευταία γραμμή ( γ) στο αρνητικούς αριθμούς. Εάν δεν υπάρχουν - βρεθεί το βέλτιστο σχέδιο, προχωράμε στο τελευταίο στάδιο της επίλυσης του προβλήματος. Εάν υπάρχει, το σχέδιο δεν είναι ακόμα βέλτιστο και ο πίνακας simplex πρέπει να υπολογιστεί εκ νέου.
Δεδομένου ότι έχουμε και πάλι αρνητικούς αριθμούς στην τελευταία γραμμή, ξεκινάμε μια νέα επανάληψη των υπολογισμών.


(10) Δεδομένου ότι δεν υπάρχουν αρνητικά στοιχεία στην τελευταία γραμμή, αυτό σημαίνει ότι βρήκαμε το βέλτιστο σχέδιο παραγωγής! Δηλαδή: θα παράγουμε εκείνα τα προϊόντα που έχουν μεταφερθεί στη στήλη "Βάση" - Χ1 και Χ2. Το κέρδος από την παραγωγή κάθε μονάδας παραγωγής είναι γνωστό ( μήτρα C) Παραμένει ο πολλαπλασιασμός των όγκων παραγωγής των προϊόντων 1 και 2 με κέρδος 1 τεμ., Παίρνουμε τον τελικό ( το μέγιστο! ) κέρδος για ένα συγκεκριμένο σχέδιο παραγωγής.
ΑΠΑΝΤΗΣΗ:
Χ1 \u003d 32 τεμ., Χ2 \u003d 20 τεμ., Χ3 \u003d 0 τεμ., Χ4 \u003d 0 τεμ.
P \u003d 48 * 32 + 33 * 20 \u003d 2 196 τρίψτε.
Galyautdinov R.R.
© Η αντιγραφή υλικού επιτρέπεται μόνο εάν υπάρχει άμεση υπερσύνδεση
| - | x 1 | + | x 2 | - | S 1 | = | 1 | ||||||||||
| x 1 | +3 | x 2 | + | S 2 | = | 15 | |||||||||||
| - | 2 | x 1 | + | x 2 | + | S 3 | = | 4 |
| - | x 1 | + | x 2 | - | S 1 | + | R 1 | = | 1 | |||||||||||
| x 1 | +3 | x 2 | + | S 2 | = | 15 | ||||||||||||||
| - | 2 | x 1 | + | x 2 | + | S 3 | = | 4 |
| x 1 \u003d 0 χ 2 \u003d 0 S 1 \u003d 0 S 2 \u003d 15 S 3 \u003d 4 R 1 \u003d 1 |
\u003d\u003e W \u003d 1 |
| x 1 | x 2 | S 1 | S 2 | S 3 | R 1 | St. ένα μέλος | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | 1: 1 = 1 |
| 1 | 3 | 0 | 1 | 0 | 0 | 15 | 15: 3 = 5 |
| -2 | 1 | 0 | 0 | 1 | 0 | 4 | 4: 1 = 4 |
| 1 | -1 | 1 | 0 | 0 | 0 | W - 1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | 1 | |
| 4 | 0 | 3 | 1 | 0 | -3 | 12 | |
| -1 | 0 | 1 | 0 | 1 | -1 | 3 | |
| 0 | 0 | 0 | 0 | 0 | 1 | W - 0 |
| - | x 1 | + | x 2 | - | S 1 | = | 1 | ||||||||||
| 4 | x 1 | + | 3 | S 1 | + | S 2 | = | 12 | |||||||||
| - | x 1 | + | S 1 | + | S 3 | = | 3 |
| x 1 | x 2 | S 1 | S 2 | S 3 | St. ένα μέλος | Θ |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 4 | 0 | 3 | 1 | 0 | 12 | 12: 4 = 3 |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | F - 1 | |
| -1 | 1 | -1 | 0 | 0 | 1 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| -1 | 0 | 1 | 0 | 1 | 3 | |
| 4 | 0 | 1 | 0 | 0 | F - 1 | |
| 0 | 1 | -1/4 | 1/4 | 0 | 4 | |
| 1 | 0 | 3/4 | 1/4 | 0 | 3 | |
| 0 | 0 | 7/4 | 1/4 | 1 | 6 | |
| 0 | 0 | -2 | -1 | 0 | F - 13 |
| S 1 \u003d 0 S 2 \u003d 0 x 1 \u003d 3 x 2 \u003d 4 S 3 \u003d 6 |
\u003d\u003e F \u003d 13 \u003d 0 \u003d\u003e F \u003d 13 |
Εξετάζεται ένα παράδειγμα λύσης της μεθόδου simplex με τη μέθοδο, καθώς και ένα παράδειγμα επίλυσης του διπλού προβλήματος.
Συνθήκη εργασίας
Για την πώληση τριών ομάδων αγαθών, μια εμπορική επιχείρηση έχει τρεις τύπους περιορισμένων υλικών και νομισματικών πόρων στο ποσό των b 1 \u003d 240, b 2 \u003d 200, b 3 \u003d 160 μονάδες. Επιπλέον, για την πώληση μιας ομάδας προϊόντων ανά χίλια ρούβλια. ο κύκλος εργασιών καταναλώνεται ένας πόρος του πρώτου τύπου σε ένα 11 \u003d 2 μονάδες, ένας πόρος του δεύτερου τύπου σε ένα 21 \u003d 4 μονάδες, ένας πόρος του τρίτου τύπου στο ποσό των 31 \u003d 4 μονάδων. Για την πώληση των 2 και 3 ομάδες αγαθών ανά χίλια ρούβλια. ο κύκλος εργασιών καταναλώνεται, αντίστοιχα, ενός πόρου του πρώτου τύπου σε ποσότητα 12 \u003d 3, 13 \u003d 6 μονάδων, ένας πόρος του δεύτερου τύπου σε ποσότητα 22 \u003d 2, 23 \u003d 4 μονάδες, ένας πόρος του τρίτου τύπου σε ποσότητα 32 \u003d 6, 33 \u003d 8 μονάδων . Κέρδη από την πώληση των τριών ομάδων αγαθών ανά χίλια ρούβλια. ο κύκλος εργασιών είναι αντίστοιχα c 1 \u003d 4, c 2 \u003d 5, c 3 \u003d 4 (χιλιάδες ρούβλια). Προσδιορίστε τον προβλεπόμενο όγκο και τη διάρθρωση του εμπορίου έτσι ώστε το κέρδος της εμπορικής εταιρείας να είναι μέγιστο.
Για το άμεσο έργο του σχεδιασμού του κύκλου εργασιών, λύσιμη μέθοδος simplexσυνθέτουν διπλή εργασία γραμμικό προγραμματισμό.
Εγκαταστήστε συζευγμένα ζεύγη μεταβλητών άμεσες και διπλές εργασίες.
Σύμφωνα με τα συζευγμένα ζεύγη μεταβλητών, από τη λύση του άμεσου προβλήματος, να λάβουμε λύση του διπλού προβλήματοςστην οποία αξιολόγηση των πόρωνπου δαπανώνται για την πώληση αγαθών.
Απλή λύση μεθόδου
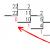
Έστω x 1, x 2, x 3 είναι ο αριθμός των πωληθέντων αγαθών, σε χιλιάδες ρούβλια, 1, 2, 3 στις ομάδες της, αντίστοιχα. Στη συνέχεια, το μαθηματικό μοντέλο του προβλήματος έχει τη μορφή:F \u003d 4 x 1 + 5 x 2 + 4 x 3 -\u003e μέγ
0))) (~) "τίτλος \u003d" (! LANG: delim (lbrace) (μήτρα (4) (1) ((2x_1 + 3x_2 + 6x_3 \u003d">!}
Λύπουμε τη μέθοδο simplex.
Εισάγουμε πρόσθετες μεταβλητές x 4 ≥ 0, x 5 ≥ 0, x 6 ≥ 0 για να μετατρέψουμε τις ανισότητες σε ίσες.

Ως βάση, πάρτε x 4 \u003d 240; χ 5 \u003d 200; x 6 \u003d 160.
Τα δεδομένα εισάγονται στο απλός πίνακας
Απλός αριθμός πίνακα 1

Στόχος λειτουργία:
 0 · 240 + 0 · 200 + 0 · 160 \u003d 0
0 · 240 + 0 · 200 + 0 · 160 \u003d 0
Υπολογίζουμε τις εκτιμήσεις με τον τύπο:

Δ 1 \u003d 0 · 2 + 0 · 4 + 0 · 4 - 4 \u003d - 4
Δ 2 \u003d 0, 3 + 0, 2 + 0, 6 - 5 \u003d - 5
Δ 3 \u003d 0 · 6 + 0 · 4 + 0 · 8 - 4 \u003d - 4
Δ 4 \u003d 0 · 1 + 0 · 0 + 0 · 0 - 0 \u003d 0
Δ 5 \u003d 0 · 0 + 0 · 1 + 0 · 0 - 0 \u003d 0
Δ 6 \u003d 0 · 0 + 0 · 0 + 0 · 1 - 0 \u003d 0
Δεδομένου ότι υπάρχουν αρνητικές αξιολογήσεις, το σχέδιο δεν είναι βέλτιστο. Η χαμηλότερη βαθμολογία:
Εισάγουμε τη μεταβλητή x 2 στη βάση.
Ορίζουμε μια μεταβλητή που ξεφεύγει από τη βάση. Για να το κάνετε αυτό, βρείτε τη μικρότερη μη αρνητική σχέση για τη στήλη x 2.
![]()
![]()
![]() = 26.667
= 26.667
Το μικρότερο μη αρνητικό: Q 3 \u003d 26.667. Αποκτήστε τη μεταβλητή x 6 από τη βάση
Η 3η γραμμή χωρίζεται από 6.
Αφαιρέστε την 3η σειρά πολλαπλασιασμένη με 3 από την 1η γραμμή
Αφαιρέστε την 3η σειρά από τις 2 φορές από τη 2η σειρά

Υπολογίζουμε:
![]()
![]()
![]()
![]()
![]()
Έχουμε ένα νέο τραπέζι:
Απλός αριθμός πίνακα 2

Στόχος λειτουργία:
 0 · 160 + 0 · 440/3 + 5 · 80/3 \u003d 400/3
0 · 160 + 0 · 440/3 + 5 · 80/3 \u003d 400/3
Υπολογίζουμε τις εκτιμήσεις με τον τύπο:

Δ 1 \u003d 0 · 0 + 0 · 8/3 + 5 · 2/3 - 4 \u003d - 2/3
Δ 2 \u003d 0 · 0 + 0 · 5 + 5 · 1 - 5 \u003d 0
Δ 3 \u003d 0 · 2 + 0 · 4/3 + 5 · 4/3 - 4 \u003d 8/3
Δ 4 \u003d 0 · 1 + 0 · 0 + 5 · 0 - 0 \u003d 0
Δ 5 \u003d 0 · 0 + 0 · 1 + 5 · 0 - 0 \u003d 0
Δ 6 \u003d 0 · (-1) / 2 + 0 · (-1) / 3 + 5 · 1/6 - 0 \u003d 5/6
Δεδομένου ότι υπάρχει αρνητική εκτίμηση Δ 1 \u003d - 2/3, το σχέδιο δεν είναι βέλτιστο.
Εισάγουμε τη μεταβλητή x 1 στη βάση.
Ορίζουμε μια μεταβλητή που ξεφεύγει από τη βάση. Για να το κάνετε αυτό, βρείτε τη μικρότερη μη αρνητική σχέση για τη στήλη x 1.

Το λιγότερο μη αρνητικό: Q 3 \u003d 40. Από τη βάση υπολογίζουμε τη μεταβλητή x 2
Διαχωρίζουμε την 3η γραμμή κατά 2/3.
Από τη 2η σειρά, αφαιρέστε την 3η σειρά φορές 8/3

Υπολογίζουμε:
![]()
![]()
![]()
Έχουμε ένα νέο τραπέζι:
Απλός αριθμός πίνακα 3

Στόχος λειτουργία:
 0 · 160 + 0 · 40 + 4 · 40 \u003d 160
0 · 160 + 0 · 40 + 4 · 40 \u003d 160
Υπολογίζουμε τις εκτιμήσεις με τον τύπο:

Δ 1 \u003d 0 · 0 + 0 · 0 + 4 · 1 - 4 \u003d 0
Δ 2 \u003d 0 · 0 + 0 · (-4) + 4 · 3/2 - 5 \u003d 1
Δ 3 \u003d 0 · 2 + 0 · (-4) + 4 · 2 - 4 \u003d 4
Δ 4 \u003d 0 · 1 + 0 · 0 + 4 · 0 - 0 \u003d 0
Δ 5 \u003d 0 · 0 + 0 · 1 + 4 · 0 - 0 \u003d 0
Δ 6 \u003d 0 (-1) / 2 + 0 · (-1) + 4 · 1/4 - 0 \u003d 1
Δεδομένου ότι δεν υπάρχουν αρνητικές αξιολογήσεις, το σχέδιο είναι βέλτιστο.
Η λύση στο πρόβλημα:
Η απάντηση
x 1 \u003d 40; x 2 \u003d 0; x 3 \u003d 0. x 4 \u003d 160; χ 5 \u003d 40; x 6 \u003d 0. Fmax \u003d 160Δηλαδή, είναι απαραίτητο να πωλήσει τα εμπορεύματα του πρώτου τύπου στο ποσό των 40 χιλιάδων ρούβλια. Τα προϊόντα του 2ου και 3ου είδους δεν χρειάζεται να πωληθούν. Στην περίπτωση αυτή, το μέγιστο κέρδος θα είναι F max \u003d 160 χιλιάδες ρούβλια.
Η λύση του διπλού προβλήματος
Η διπλή εργασία έχει τη μορφή:
Ζ \u003d 240 · y 1 + 200 · y 2 + 160 · y 3 -\u003e min
(2y_1 + 4y_2 + 4y_3\u003e \u003d 4) (3y_1 + 2y_2 + 6y_3\u003e \u003d 5) (6y_1 + 4y_2 + 8y_3\u003e \u003d 4) (y_1, y_2, y_3\u003e \u003d 0))) (~)">!}
Εισάγουμε επιπλέον μεταβλητές y 4 ≥ 0, y 5 ≥ 0, y 6 ≥ 0 για να μετατρέψουμε τις ανισότητες σε ίσες.

Τα συζευγμένα ζεύγη μεταβλητών των άμεσων και διπλών προβλημάτων έχουν τη μορφή:
Από το τελευταίο απλό παράδειγμα του πίνακα αριθ. 3 του άμεσου προβλήματος, βρίσκουμε τη λύση του διπλού προβλήματος:
Z min \u003d Fmax \u003d 160;
y 1 \u003d Δ 4 \u003d 0, y2 \u003d Δ5 \u003d 0; y3 \u003d Δ6 \u003d 1; γ4 \u003d Δ1 \u003d 0; y5 \u003d Δ2 \u003d 1; y6 \u003d Δ3 \u003d 4;
Εξετάστε simplex μέθοδο για την επίλυση προβλημάτων γραμμικού προγραμματισμού (LP). Βασίζεται στη μετάβαση από ένα σχέδιο αναφοράς σε ένα άλλο, στο οποίο η τιμή της αντικειμενικής συνάρτησης αυξάνεται.
Ο αλγόριθμος simplex έχει ως εξής:
- Μεταφράζουμε το αρχικό πρόβλημα στην κανονική μορφή εισάγοντας πρόσθετες μεταβλητές. Για τις ανισότητες της μορφής ≤, εισάγονται επιπλέον μεταβλητές με το σύμβολο (+), ενώ για την ανισότητα ≥, τότε με το σύμβολο (-). Πρόσθετες μεταβλητές εισάγονται στην αντικειμενική λειτουργία με τις αντίστοιχες πινακίδες με συντελεστή ίσο προς 0 γιατί η αντικειμενική λειτουργία δεν θα πρέπει να αλλάξει την οικονομική της σημασία.
- Vector διαγράφονται P i των συντελεστών για τις μεταβλητές και μια στήλη των ελεύθερων όρων. Αυτή η ενέργεια καθορίζει τον αριθμό των διανυσμάτων μονάδας. Ο κανόνας - πρέπει να υπάρχουν όσο το δυνατόν περισσότεροι διανύσματα μονάδων καθώς υπάρχουν ανισότητες στο σύστημα περιορισμού.
- Μετά από αυτό, τα αρχικά δεδομένα εισάγονται στον απλό πίνακα. Οι φορείς μονάδας εισάγονται στη βάση και εξαιρώντας τους από τη βάση, βρίσκουν τη βέλτιστη λύση. Οι συντελεστές της αντικειμενικής συνάρτησης γράφονται με το αντίθετο σημείο.
- Ένα κριτήριο βέλτιστου για το πρόβλημα LP - η λύση είναι βέλτιστη εάν στο στ - Όλοι οι συντελεστές είναι θετικοί. Υποδεικνύεται ο κανόνας για την εύρεση της στήλης ανάλυσης στ - η γραμμή και μεταξύ των αρνητικών στοιχείων της το μικρότερο επιλέγεται. Vector P i το περιεχόμενό του γίνεται επιτρεπτό. Ο κανόνας για την επιλογή ενός στοιχείου επίλυσης - οι σχέσεις των θετικών στοιχείων της στήλης διαχωρισμού με τα στοιχεία του διανύσματος καταρτίζονται P 0 και ο αριθμός που δίνει τη μικρότερη αναλογία γίνεται το στοιχείο διαχωρισμού σε σχέση με το οποίο ο πίνακας simplex θα υπολογιστεί εκ νέου. Η συμβολοσειρά που περιέχει αυτό το στοιχείο ονομάζεται συμβολοσειρά επιδιόρθωσης. Εάν δεν υπάρχουν θετικά στοιχεία στη στήλη ανάλυσης, τότε το πρόβλημα δεν έχει λύση. Μετά τον προσδιορισμό του στοιχείου επίλυσης, προχωρούν στη μνεία του νέου πίνακα simplex.
- Κανόνες για τη συμπλήρωση ενός νέου πίνακα simplex. Μια μονάδα τοποθετείται στη θέση του επιτρέποντος στοιχείου και άλλα στοιχεία θεωρούνται ίσα 0 . Ο διάνυσμα διαχωρισμού εισάγεται στη βάση από την οποία αποκλείεται ο αντίστοιχος μηδενικός φορέας, και οι υπόλοιποι φορείς βάσης γράφονται αμετάβλητοι. Τα στοιχεία της γραμμής δικαιωμάτων διαιρούνται με το στοιχείο επίλυσης και τα υπόλοιπα στοιχεία υπολογίζονται σύμφωνα με τον κανόνα των ορθογωνίων.
- Έτσι κάνουμε μέχρι στ - όλα τα στοιχεία δεν θα γίνουν θετικά.
Ας εξετάσουμε τη λύση του προβλήματος χρησιμοποιώντας τον αλγόριθμο που εξετάστηκε παραπάνω.
Δεδομένου:
Φέρνουμε το πρόβλημα στην κανονική μορφή:

Κατασκευάζουμε το διάνυσμα:

Συμπληρώνουμε τον πίνακα simplex:

:
Εκ νέου υπολογισμός του πρώτου στοιχείου του διανύσματος P 0, για το οποίο κάνουμε ένα ορθογώνιο αριθμών: και παίρνουμε:  .
.
Εκτελούμε παρόμοιους υπολογισμούς για όλα τα άλλα στοιχεία του πίνακα simplex:

Στο ληφθέν σχέδιο στ - Η γραμμή περιέχει ένα αρνητικό στοιχείο - (-5/3), του διανύσματος P 1. Περιέχει στη στήλη του ένα θετικό στοιχείο, το οποίο θα είναι το στοιχείο επίλυσης. Ας υπολογίσουμε εκ νέου τον πίνακα σχετικά με αυτό το στοιχείο:

Η απουσία αρνητικών στοιχείων στο στ - βρέθηκαν μέσα γραμμής βέλτιστο σχέδιο:
F * \u003d 36/5, Χ \u003d (12/5, 14/5, 8, 0, 0).
- Ashmanov S. Α. Γραμικός Προγραμματισμός, Μόσχα: Nauka, 1998,
- Ventzel Ε.δ. Επιχειρησιακή Έρευνα, M: Soviet Radio, 2001,
- Kuznetsov Yu.N., Kuzubov V.I., Voloshenko Α.Β. Μαθηματικός Προγραμματισμός, M: Ανώτατο Σχολείο, 1986
Προσαρμοσμένη Γραμμική Λύση Προγραμματισμού
Μπορείτε να παραγγείλετε οποιεσδήποτε εργασίες στον τομέα αυτό στην ιστοσελίδα μας. Μπορείτε να επισυνάψετε αρχεία και να καθορίσετε τις ημερομηνίες